What Is the Particle in a Box Model in Quantum Mechanics?

By Atif SuhailReviewed by Louis CastelNov 14 2025

The particle in a box is one of the simplest and most influential models in quantum mechanics. It imagines a particle that is completely free to move inside a finite region of space, but absolutely forbidden from escaping because the potential energy outside that region is taken to be infinite.¹

Image Credit: Max100ka/Shutterstock.com

Despite its simplicity, the model is foundational. It is often the first non-trivial system for which students solve the Schrödinger equation exactly, and it beautifully illustrates core quantum ideas: the wave nature of matter, the emergence of quantized energy levels, and the crucial role of boundary conditions in determining allowed states.¹

In addition, the model is not just a pedagogical toy. With appropriate reinterpretation, it provides a remarkably good first description of electrons confined in nanoscale structures such as quantum dots and quantum wells, where spatial confinement leads directly to modified electronic and optical properties.¹

Historical and Theoretical Context

The particle in a box model emerged in the early decades of the twentieth century, when quantum mechanics was being constructed by figures such as Erwin Schrödinger, Werner Heisenberg and Paul Dirac. Schrödinger’s wave equation, published in 1926, provided a differential equation for the wavefunction of a quantum particle, and simple potentials such as an infinite well offered solvable examples that could be compared with emerging experimental results.²

Early quantum theory faced a conceptual challenge: everyday intuition, built from classical mechanics, fails at the atomic scale. Simplified models such as the harmonic oscillator, hydrogen atom, and particle in a box became indispensable “laboratories of the mind”. They strip away complications and focus on a few essential features: confinement, boundary conditions, and the relation between allowed energies and spatial structure of the wavefunction.²

These elementary models proved extraordinarily influential. Many more sophisticated approaches, including band structure theory, quantum defect methods and numerical simulations, still borrow ideas and approximations that can be traced back to such textbook systems.²

How the Model Works?

The canonical example is the one-dimensional infinite well. A particle of mass m is confined between two impenetrable walls at x = 0 and x = L. The potential is

                        V(x) = 0            for 0 < x < L and infinite otherwise.

Inside the box the time independent Schrödinger equation is

- (h² / 2m) (d²ψ(x) / dx²) = E ψ(x),

subject to the boundary conditions ψ(0) = ψ(L) = 0, since the wavefunction must vanish at infinite potential barriers.²

Solving this eigenvalue problem yields sinusoidal wavefunctions and discrete energy eigenvalues, that is the eigenvalues of the Hamiltonian,

ψ?(x) = √(2/L) sin(nπx/L),         E? = n²h² / (8mL²), for n = 1, 2, 3, ...

Here

• the wavefunction ψ_n(x) encodes the probability amplitude of finding the particle at position x,
• the boundary conditions restrict the allowed forms of ψ?, enforcing nodes at the walls,
• the eigenvalues E_n represent the quantized energy levels,
• quantization arises from the requirement that the wavefunction fit an integer number of half wavelengths between the walls.

A particularly striking result is the absence of a zero-energy state. The lowest energy corresponds to n = 1:

E1 = h² / (8mL²) ≠ 0,

the so called zero-point energy. Even in its ground state, the particle cannot be at rest, because that would violate the uncertainty principle. Confinement necessarily implies intrinsic kinetic energy.²

Real-World Applications and Quantum Confinement

While an infinite well is idealized, real materials can approximate this situation when particles are confined to regions on the nanometer scale. This leads to quantum confinement, where reducing the size of a system changes its allowed energy levels and thus its optical and electronic behaviour.

A prime example is the semiconductor quantum dot, a nanocrystal of materials such as CdSe, ZnS, or GaAs with diameters in the 2–10 nm range. Electrons and holes are effectively trapped within the dot by potential barriers at the surface, similar to a particle in a three-dimensional box. In such systems:

• Energy levels in the conduction and valence bands become discrete rather than continuous.
• The effective band gap increases as the dot size decreases.
• Optical absorption and emission spectra show a blue shift for smaller dots and a red shift for larger ones.

For CdSe quantum dots, the emission color can be tuned across the visible range simply by changing the dot radius: smaller dots emit toward the blue/green, larger dots toward orange/red. This makes them valuable in displays, LEDs, and bio-imaging probes.³

The same basic idea appears in quantum wells and superlattices (e.g. GaAs/AlGaAs heterostructures used in lasers), in 2D materials where electrons are confined to atomically thin layers, and in photonics and optoelectronics, where tailored confinement allows engineers to design devices with specific absorption or emission wavelengths. The particle-in-a-box formula, suitably modified for finite barriers and effective masses, often provides a surprisingly good first estimate of these confinement energies.³

Extensions and Variations of the Model

The classic one-dimensional (1D) particle-in-a-box model can be extended in several important ways to better reflect real-world quantum systems.

First, moving to two- or three-dimensional confinement leads to quantized energy levels of the form
En_x,n_y,n_z    proportional to n_x² / L_x² + n_y² / L_y² + n_z² / L_z²,

where 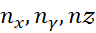are quantum numbers and are the respective box dimensions. This extension is directly applicable to systems like rectangular quantum wells, wires, and dots, where electrons are confined in multiple directions.

Replacing the idealized infinite potential walls with large but finite barriers introduces finite potential wells,offering a more realistic framework for modeling electron confinement in semiconductor heterostructures. In these systems, wavefunctions extend slightly beyond the well boundaries, resulting in both bound states and tunneling behavior.

Asymmetric wells provide yet another refinement. Varying the widths of the wells or the heights of the barriers allows for the modeling of more complex structures such as coupled quantum wells. These systems exhibit phenomena like energy level splitting and inter-well tunneling due to the coupling between wells.

Finally, introducing spin and external fields, such as spin–orbit coupling, magnetic fields, or electric fields,adds further complexity. These factors lead to effects like Zeeman and Stark shifts, as well as spin-dependent energy structures, and are crucial for accurately describing many modern nanodevices.⁴

For spherical quantum dots, the “box” is effectively replaced by a sphere and the electron and hole masses are replaced by their effective masses in the crystal lattice. Even with these modifications, one still obtains confinement energies that scale roughly as (1/R²) (with (R) the dot radius), in close analogy with the 1D box formula.^{1, 4}

Limitations and Pedagogical Use

The particle in a box model is intentionally stripped down, and its limitations are significant. It treats a single, non-interacting particle, whereas real materials contain many interacting electrons and holes. The boundaries are taken to be perfectly rigid and abrupt, while actual potentials are finite and often vary in space. Moreover, the model ignores particle particle interactions, phonons, disorder and many body effects, all of which can play a dominant role in real condensed matter systems.⁵

Yet these simplifications are exactly what make the model so valuable in teaching. In a single, analytically solvable example, students learn how boundary conditions quantize energy, how to normalize wavefunctions, how probabilities are extracted from (|ψ|²), and why zero-point energy is unavoidable.⁶

Additionally, the model acts as a conceptual bridge: once one understands confinement in an ideal box, it is easier to appreciate systematic corrections, effective mass approximations, finite barriers, Coulomb interactions, or spin. Consequently, the particle in a box remains a mainstay of introductory quantum mechanics courses and outreach articles aimed at building intuition for quantum phenomena.⁶

Future Developments and Quantum Technology Implications

Although introduced almost a century ago, the particle in a box model continues to serve as a foundational concept for many modern quantum technologies. Confinement of electrons and holes in semiconductor nanostructures is central to qubits in quantum dots, quantum dot lasers, single photon sources and advanced photodetectors, where energy level spacing and device performance are governed by confinement physics.

Very fast quantum sensors and other quantum optical technologies also exploit discrete levels in confined systems. Even when detailed numerical simulations are used, the particle in a box remains a basic conceptual prototype for understanding and designing such nanoscale quantum devices.

Want to brush up on particle pairing? Read on here

References and Further Readings

1. Balakrishnan, V., Particle in a Box: A Basic Paradigm in Quantum Mechanics - Part 2. Resonance 2022, 27, 1327-1340.
2. Onyia, A.; Ikeri, H.; Nwobodo, A., Theoretical Study of the Quantum Confinement Effects on Quantum Dots Using Particle in a Box Model. Journal of Ovonic Research 2018, 14, 49-54.
3. García de Arquer, F. P.; Talapin, D. V.; Klimov, V. I.; Arakawa, Y.; Bayer, M.; Sargent, E. H., Semiconductor Quantum Dots: Technological Progress and Future Challenges. Science 2021, 373, eaaz8541.
4. Hoekzema, D.; van den Berg, E.; Schooten, G.; van Dijk, L., The Particle/Wave-in-a-Box Model in Dutch Secondary Schools. Physics education 2007, 42, 391.
5. Ellerman, D., Quantum Mechanics over Sets: A Pedagogical Model with Non-Commutative Finite Probability Theory as Its Quantum Probability Calculus. Synthese 2017, 194, 4863-4896.
6. McAfee, S. C.; Watts, F. M.; Rodriguez, J.-M. G., A Review of Research on the Teaching and Learning of Quantum Mechanics. Chemistry Education Research and Practice 2025, 26, 578-593.

Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.