In a recent paper published in Quantum Reports, the author introduced a new quantum theory for Lee–Naughton–Lebed (LNL) angular oscillations, specifically addressing their behavior in moderately strong electric fields.
 Study: Quantum Theory Explains LNL Conductivity Oscillations. Image Credit: Monika Wisniewska/Shutterstock.com
Study: Quantum Theory Explains LNL Conductivity Oscillations. Image Credit: Monika Wisniewska/Shutterstock.com
Background
Organic conductors with quasi-one-dimensional (Q1D) Fermi surfaces exhibit distinctive magnetic properties due to Bragg reflections of moving electrons from the Brillouin zone boundaries under strong and moderate magnetic fields. These properties include LNL angular oscillations, Lebed's magic angles, the three-dimensional (3D) quantum Hall effect, and field-induced spin (charge)-density-wave phase diagrams.
Among these phenomena, Lebed's magic angles are particularly complex. In contrast, the field-induced spin (charge)-density waves, LNL angular oscillations, and the 3D quantum Hall effect have been successfully explained within the framework of the Landau Fermi liquid (FL) theory. Notably, the LNL effect has been effectively addressed through theoretical models.
For instance, the expression obtained in studies considering a layered Q1D conductor with the electron spectrum was,
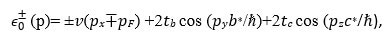
In this expression, the first represented the conducting chains’ electron-free motion on the left (−) and right (+) sheets of the Q1D Fermi surfaces, with vF and pF being the Fermi velocity and Fermi momentum, respectively.
Additionally, the second and the third terms corresponded to the electron hopping in the perpendicular axes, c∗and b∗, ℏ is the Planck constant, p is the total electron momentum, px is its component along conducting chains, and pz and py are the electron momentum components along c∗and b∗ axes, respectively.
Moreover, the LNL phenomenon has been experimentally investigated in a recent study (Kobayashi et al.) in strong electric fields, The results showed that the LNL conductivity maxima were split by the strong electric field in an α-(ET)2-based organic conductor. A hypothetical theoretical formula describing the experimental splitting was also suggested in the study.
The Study
In this study, the researcher proposed a quantum mechanical theory for LNL angular oscillations in moderately strong electric fields for the first time. A quasi-classical expression for conductivity was derived, addressing the splitting of LNL conductivity maxima observed experimentally under strong magnetic and moderately strong electric fields.
The researchers showed that their theoretical formula accurately describes the experimental results reported in recent studies. Initially, the quasi-classical Peierls substitution was applied to model electron motion along the conducting chains without considering electric and magnetic fields.
The electric field was then introduced as a small perturbation to the Hamiltonian along the least conductive zzz-axis, and the Peierls substitution was reapplied. Following this, the magnetic field was incorporated into the electron velocity operator and the electron Hamiltonian.
The Kubo formula for conductivity was used, leveraging known eigenvalues of velocity operators and electron wave functions. This approach led to the derivation of an expression for the total conductivity in strong electric fields, accounting for the presence of an inclined magnetic field.
Study Contributions
The principal contribution of this study was the derivation of a quasi-classical expression for conductivity, which had previously only been hypothesized in the work of Kobayashi et al. This equation, however, has limited applicability and is not suitable for very strong electric fields.
Specifically, the derived equation was applicable for lower experimentally used voltages (V0 ≃ 2 V) and not applicable for higher experimentally used voltages (V0 ≃ 20 V). The results obtained were general for all Q1D conductor families.
The splitting of LNL conductivity maxima was attributed to changes in the Lorentz force's sign between the right and left segments of the Q1D Fermi surfaces, resulting from the sign change in electron velocity, while the electric force remained unchanged.
Thus, it is essential to apply and analyze the novel equations derived in this study with typical Q1D conductor types, such as the tetramethyltetraselenafulvalene (TMTSF)2X conductors, is crucial. The LNL oscillations could be effectively investigated in (TMTSF)2PF6, where c* = 1.36 nm.
Moreover, the LNL conductivity maxima splitting must be observed in a similar electric field range as observed by Kobayashi et al. in the α-(ET)2-based conductor. The evident experimental problem was to identify a way to avoid the (TMTSF)2PF6 sample overheating. Similarly, the Peierls substitution method must be used at magnetic fields lower than the magnetic breakdown field for the (TMTSF)2ClO4 conductor.
In summary, this work demonstrated that the quantum theory proposed can effectively explain the LNL angular effect in moderately strong electric fields.
Journal Reference
Lebed, A. G. (2024). Quantum Theory of Lee–Naughton–Lebed’s Angular Effect in Strong Electric Fields. Quantum Reports, 6(3), 359-365. DOI: 10.3390/quantum6030023, https://www.mdpi.com/2624-960X/6/3/23
Kobayashi, K., Saito, M., Ohmichi, E., Osada, T. (2006). Electric-Field Effect on the Angle-Dependent Magnetotransport Properties of Quasi-One-Dimensional Conductors. Physical review letters, 96(12), 126601. DOI: 10.1103/PhysRevLett.96.126601, https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.96.126601
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.