A collaborative effort from TU Wien, alongside teams from the United States and Switzerland, has demonstrated that artificial intelligence can significantly advance progress in integrating quantum theories into computer simulations.
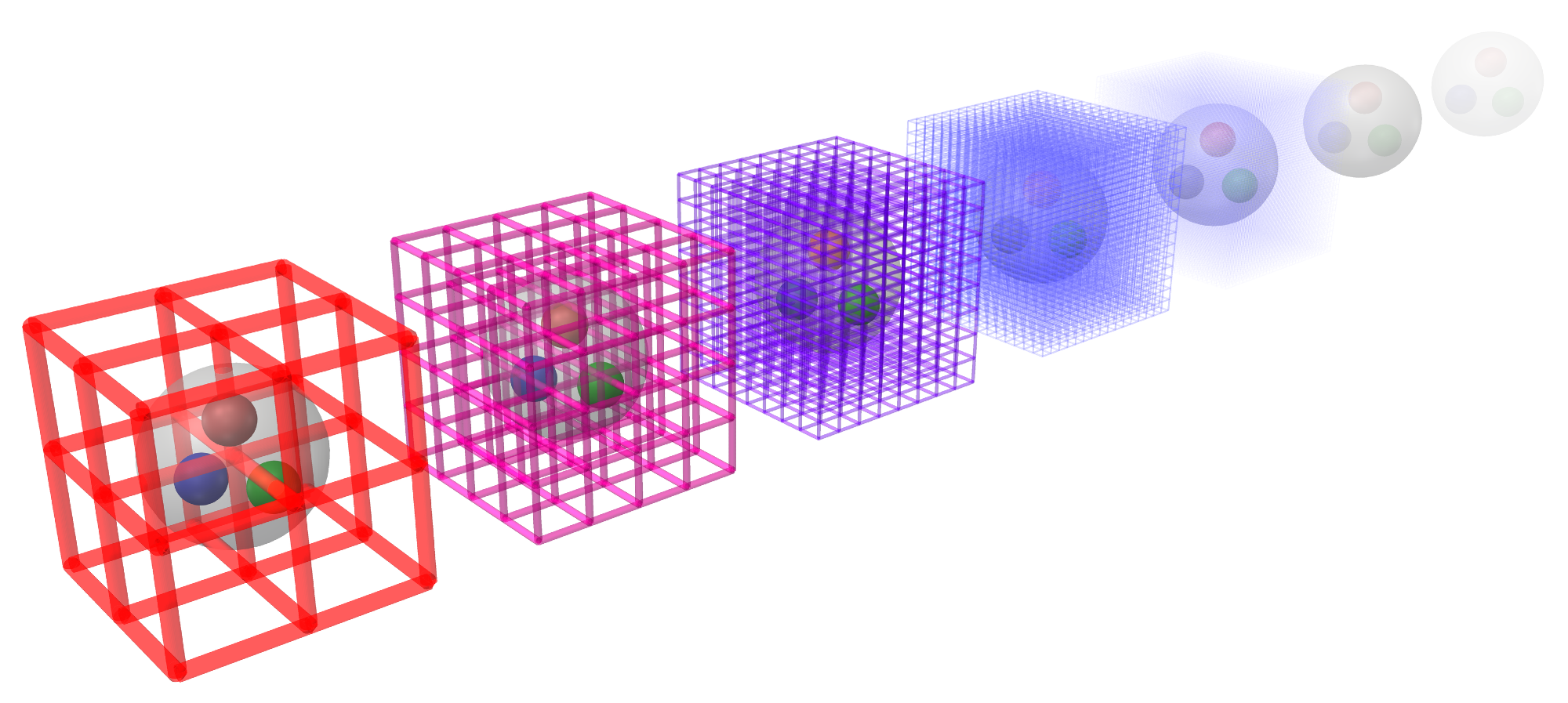 In quantum field theory on a computer, what happens to the result as you make the calculation grid increasingly finer? Image Credit: TU Wien
In quantum field theory on a computer, what happens to the result as you make the calculation grid increasingly finer? Image Credit: TU Wien
This question touches on some exceptionally challenging issues. Quantum field theories can be expressed in multiple ways when implemented on a computer. In principle, all of these formulations should yield the same physical predictions, though they may rely on vastly different approaches. Some are computationally impractical, either due to inefficiency or lack of precision, while others turn out to be surprisingly effective.
In the Computer, the Whole World is a Grid
If we want to work with quantum field theories on a computer, we have to discretize them. That's actually nothing unusual.
David Müller, Institute for Theoretical Physics, TU Wien
Every image displayed on a computer screen is made up of tiny, individual pixels; similarly, when determining the trajectory of a lunar rocket, the calculations are executed in small, distinct time intervals.
The same principle applies in particle physics: A four-dimensional lattice is constructed, comprising three spatial dimensions and one temporal dimension. Each point on the lattice is recorded on the computer, and the principles of quantum field theory govern the interactions between these lattice points. This methodology allows for the simulation of events such as massive particle collisions at CERN or the behavior of matter shortly after the Big Bang.
In quantum field theory, both space and time are treated as continuous entities. However, when these theories are represented on a discrete lattice, there are certain degrees of freedom available: Various lattice theories can correspond to the same continuous theory.
It is essential to choose a variant that offers the highest likelihood of computational success. Failing to do so may result in the computer simulation reaching an impasse, thereby preventing it from arriving at the correct solution within a feasible timeframe.
Different Scale, Same Result
An important key to success is the so-called fixed-point equations.
There are certain formulations of quantum field theory on a lattice that have a particularly nice property.
Urs Wenger, University of Bern
“They ensure that certain properties remain the same, even if we make the lattice coarser or finer. If this is the case, we know: This property is reliable, it also agrees at coarse resolution, i.e., on a wide-mesh grid, with the continuum that would correspond to an infinitely fine grid,” said Wenger.
It’s a bit like using maps at different scales, not every detail appears the same across versions. Still, some features remain consistent no matter the resolution. For example, neighboring countries stay the same regardless of how zoomed in or out the map is.
This indicates that one can be fairly confident that this characteristic, if it is not influenced by the map scale, is also a characteristic of reality itself.
The Success of AI
For 30 years, researchers have worked to adapt these lattice formulas, but the hundreds of thousands of variables involved make the task impossible for humans to handle alone.
Many people began exploring these concepts three decades ago, but back then, we simply didn't have the technical means. By joining forces with the team at TU Wien, we were finally able to revisit these long-standing ideas.
Kieran Holland, University of the Pacific
The team has successfully created a unique neural network tailored specifically for this objective. Off-the-shelf AI solutions do not achieve the desired outcome; it was essential to design artificial intelligence that ensures adherence to the physical laws defined from the beginning.
The team has now accomplished this task. The outcome of their efforts: The action (a key physical quantity in quantum field theories, also known from Planck’s concept of the “quantum of action”) has been parameterized on a lattice using AI in a way that allows even coarse grids to yield surprisingly small errors.
“We were able to show that this approach opens up a completely new way to simulate complex quantum field theories with manageable computational effort,” said Andreas Ipp, TU Wien.
Sources:
Journal Reference:
Holland, K., et al. (2026) Machine-Learned Renormalization-Group-Improved Gauge Actions and Classically Perfect Gradient Flows. Physical Review Letters. DOI: 10.1103/k41k-2pnc. https://journals.aps.org/prl/abstract/10.1103/k41k-2pnc
TU Wien