Feb 17 2016
Mikhail Lemeshko and Richard Schmidt introduce technique to calculate and understand "angulon problem" • paper published in Physical Review X
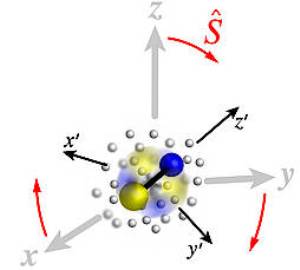
The concepts of rotation and angular momentum play a crucial role in many areas of physics, ranging from nuclear spectroscopy to molecular collisions and precision measurements. In a paper appearing in the leading physics journal Physical Review X on February 12, 2016, Mikhail Lemeshko, Professor at the Institute of Science and Technology Austria (IST Austria), and Richard Schmidt, Postdoc at Harvard University, introduce a technique to understand and calculate angular momentum in settings where many particles interact with each other, so-called many-particle systems.
In the last 70 years, the quantum theory of angular momentum has been successfully used to describe the properties of nuclei, atoms and molecules. However, in most situations occurring in nature particles interact with each other, which makes it challenging to understand and calculate the angular momentum properties even for small systems. This applies in particular to realistic experiments where nuclei, atoms and molecules are almost never isolated. Instead, they are disturbed by their surrounding environment, be it a gas, a solution or lattice vibrations in a crystal. In such a situation, the angular momentum can be redistributed between infinitely many quantum particles. Therefore, such settings are intractable using currently available mathematical approaches.
In their paper, Lemeshko and Schmidt introduce a new mathematical technique to calculate and understand the transfer of angular momentum between a rotating impurity and a quantum many-particle system — so-called “angulon problem.” The technique is based on a novel canonical transformation that removes the complex algebra involved in the problem and thereby drastically simplifies the understanding of angulon physics. Potentially, this technique can be applied to a broad range of problems in atomic, condensed matter, and chemical physics.