Quantum Fundamentals – The Uncertainty Principle

By Ibtisam AbbasiReviewed by Louis CastelJun 24 2025

The Uncertainty Principle is among the core concepts differentiating the quantum world of physics from the classical concepts of space, and time. In short, the Uncertainty principle states that the position and momentum (velocity) states of any object can’t be precisely quantified simultaneously.¹ The idea of quantum uncertainty was proposed by famous physicist Werner Heisenberg in 1927. It ushered quantum science into a new era of theoretical physics, paving the way for major scientific inventions like ultra-fast quantum computers.

Image Credit: Natali art collections/Shutterstock.com

What is the Uncertainty Principle?

The Uncertainty Principle, also known as the Heisenberg Uncertainty Principle, is a fundamental idea in quantum physics. It states that if an object's position is measured with high precision, its complementary properties, such as momentum (or velocity), cannot be known with equal accuracy at the same time.

W. Heisenberg explained in his paper that, in contrast to the classical physical theory, quantum theory is essentially a statistical theory, allowing for statistical calculations based on probability. In this regard, the present state of any object, in terms of all its parameters, can’t be known completely and accurately.

Mathematically, this concept is represented as:

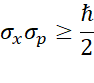
In the above equation, 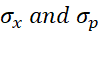 are the standard deviation in position x and momentum p respectively, while  is Planck’s constant.²

The Uncertainty Principle can also be expressed this way: the precision with which two quantum properties of a particle can be measured at the same time is fundamentally limited. Specifically, the product of the standard deviations, or uncertainties, of these related quantities must be on the order of Planck’s constant. Experts have predicted that this quantum uncertainty only exists for coupled or conjugated quantum variables.³

Using the experimental results of the Dirac-Jordan Theory and other quantum experiments, Heisenberg estimated that the inability to accurately determine the position and momentum (or any two coupled quantum parameters) of a particle simultaneously, is an inherent uncertainty.

In any experimental setup to determine the position and momentum of a particle at the same instant, the uncertainty would exist, no matter how theoretically perfect the experimental technique or how carefully calibrated the instruments are. The simultaneous measurement of canonically conjugated quantum parameters is always limited by the intrinsic quantum uncertainty features.

Download your PDF copy now!

Mathematical and Conceptual Foundations

The Dirac-Jordan theory is highly applicable for quantum calculations as it defines the interconnection between variables in such a way that any quantum parameter can be defined as a diagonal matrix. These matrices can also be visualized as tensors in multidimensional space, and the relationship between these tensors can be defined by mathematical equations.

The coordinate system for developing the mathematical relationship can be placed along the main axes of any of the one tensors. Mathematical transformation formulae can be determined to develop the system of coordinates oriented along the main axes of one tensor A into the one oriented along the other tensor B. This transformation corresponds to the basics of the Schrödinger equation.⁴

Importance of Schrödinger Equation and Wave-Particle Duality

For an object of mass m, its position at any time t can be represented by x(t), while its momentum (p) and velocity in classical physics can be calculated from the position x(t), by Newton’s second law. In quantum physics, the Schrödinger equation provides information regarding the quantum states of an object, giving the waveform, which gives us basically the probability of finding the particle at a certain position.

The Schrödinger equation makes use of the wave nature of particles, highlighting the dual nature of sub-atomic particles. Schrödinger assumed that a particle can be considered like a wave, continuously evolving in the space-time following the wave equation.

The uncertainty principle is the result of the wave-particle duality, stating that a body could be a wave or a particle at any instant, making it impossible to determine both its position and momentum at the same time. The interconnection between the space-time attributes and the energy momentum of the elementary particles forms the basis for the uncertainty principles, explained mathematically using the de-Broglie internal wave expressions.⁵

Importance of Planck’s Constant

The de Broglie formula provides a relationship between the wavelength (l) of the quantum particle wave to the momentum (p) by:

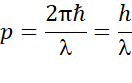
So, the associated wavelength of the quantum particle is associated with its momentum in the order of Planck’s constant. As stated above, the product of uncertainties of conjugated parameters is of the order of Planck’s constant, which means that Planck’s constant is the lowest limit possible to characterize the limit of quantum uncertainty in the simultaneous measurement of position and momentum. If Planck’s constant goes to zero, the quantum model would have zero intrinsic uncertainty and it would then be characterized as a classical theoretical atomic model. Furthermore, Neil Bohr stated that the Planck’s constant is essential for expressing the stability of electrons, and ensuring they do not collapse into their orbits. So, apart from being at the core of wave-particle duality, and uncertainty principles, the Planck’s constant is key for conceptualizing the concepts of modern quantum physics.⁶

Case Study for Explaining Uncertainty Principle

Heisenberg in his paper has illustrated the uncertainty principle using the example of a Gamma-ray microscope to measure the position of an electron. The light is diffracted from the electron, and the scattered light induces the Compton Effect.

When the position of the electron is to be measured, the instant at which diffraction of light from the electron occurs, energy is transferred to the electron, and its momentum shifts discontinuously. If a smaller wavelength of light is used to determine the position of the electron more precisely, the shift in momentum would be increasingly rapid. For a light with a larger wavelength, the shift in momentum of the electron is much less.

This highlights that at the instance of determining the position of an electron, the momentum shifts rapidly and can only be known in the order of magnitude of the discontinuous change. In simple words, the more precise and accurate the position of an electron is determined, the more uncertainty would occur in the determination of momentum.⁷

Technology Review

Traditionally, public cryptographic algorithms utilized NP-hard techniques like integer factorization in RSA and the discrete logarithm in Diffie-Hellman. However, recently quantum cryptography using Heisenberg’s uncertainty principle will make these classical platforms obsolete.

Fault-tolerant quantum computers using uncertainty principles are maturing rigorously. In this regard, quantum key distribution (QKD), extensively using quantum uncertainty for the functionality of quantum bits (qubits), provides information-theoretic security.

The shift to modern quantum computing is becoming popular as experts want cryptographic security platforms to function using quantum uncertainty principles. This shift could make the domain of quantum cryptography a major industry in the future with highly efficient techniques like quantum symmetric encryption, post-quantum cryptography, and quantum encryption methods used in phase space for coherent optical communication.⁸ Additionally, the uncertainty principle is also used for the characterization of device-independent randomness involving certifying the randomness obtained by the use of untrusted devices.⁹

Experimental Evidence

Over the years, many experimental verifications of Heisenberg’s uncertainty principles have been performed cementing it as the core of modern quantum computing.

A tested way to verify the Uncertainty principle is by the use of Single-slit diffraction of Helium-Neon laser. Generally, lasers operating with wavelengths between 630 – 650 nm are used to pass laser waves through a slit of known width on an optical bench. The photodetector scans the resulting diffraction pattern, making a plot of the intensity with the position. The minima of the diffraction patterns show an intensity pattern matching Kirchhoff’s diffraction theory, with narrower slits leading to broader diffraction patterns, validating the inverse relationship.

In a novel approach, experts have used nuclear-spin qubits in a new approach to verify Heisenberg’s uncertainty principle. As stated above, when light is used to measure the position of the electron, its momentum changes and leads to uncertainties in its determination. In the experimental verification, the research team verified the uncertainties by quantifying them geometrically.¹⁰

The experts reformulated the framework devised an improved formula for qubit measurements, and used a nuclear-spin qubit system for experimental testing. Two compatible observables were used to simulate two completely incompatible observables' position and momentum. The results verified that the more incompatible the quantum parameters are with each other, the more uncertainties were observed in their measurements.¹¹

Future Interpretations

The uncertainty principle is being researched extensively due to its importance and to ensure highly efficient next-gen quantum information processing systems. In this regard, entropies are becoming widely popular and an accurate way of expressing quantum uncertainties quantitatively.

Entropic uncertainty relations (EURs) establish lower bounds on the uncertainty about the outcomes of quantum measurements. In the future, experts have predicted that EURs to become a key tool for analyzing quantum security protocols.¹² In addition to their role in security, EURs can also be used to reveal genuinely non-classical characteristics of quantum systems, making it key for future highly sensitive low latency sensors.

Even after more than 90 years, Heisenberg’s quantum uncertainty principle is being researched all over the world, enabling us to enter a new era of modern physics.

Further Reading

1. Hilgevoord, J. (2016). The Uncertainty Principle. The Stanford Encyclopedia of Philosophy. The Metaphysics Research Lab, Stanford University. [Online]. Available at: https://plato.stanford.edu/entries/qt-uncertainty/ [Accessed on: June 15, 2025].
2. Griffiths, D. (1995). Read College. Introduction to Quantum Mechanics. 2nd Edition. Prentice Hall, Inc. 1-20.
3. Robertson, H. (1929). The uncertainty principle. Physical Review. 34(1). 163. Available at: https://doi.org/10.1103/PhysRev.34.163
4. Duncan, A.  et. al. (2013). (Never) Mind your p’s and q’s: Von Neumann versus Jordan on the foundations of quantum theory. The European Physical Journal H, 38(2), 175-259. Available at:  https://doi.org/10.1140/epjh/e2012-30024-5
5. Bezverkhniy, V. et. al. (2021).  Heisenberg's Uncertainty Principle and Wave-Particle Dualism . Available at: http://dx.doi.org/10.2139/ssrn.3865301
6. Khongngain, L. (2023). Revisiting the significance of Planck’s constant in quantum mechanics. International Journal of Scientific Research in Physics and Applied Sciences, 11(6), 9-12. Available at: https://doi.org/10.26438/ijsrpas/v11i6.912
7. Heisenberg, W. (1927). Uber den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik, Zeit schrift fur Physik. 43(3-4). 172-198. Available at: https://doi.org/10.1007/BF01397280
8. Kuang, R. (2023). Generalized Uncertainty Principles for Quantum Cryptography. arXiv preprint arXiv:2302.01026. Available at: https://doi.org/10.48550/arXiv.2302.01026
9. Coles, P. et. al. (2017). Entropic uncertainty relations and their applications. Reviews of Modern Physics. 89(1). 015002. Available at: https://doi.org/10.1103/RevModPhys.89.015002
10. Zyga, L. (2016). Experimental test verifies Heisenberg's measurement uncertainty principle. Quantum Physics. Phys.org. Available at: https://phys.org/news/2016-06-experimental-heisenberg-uncertainty-principle.html [Accessed on: June 19, 2025].
11. Ma, W. et. al. (2016). Experimental test of Heisenberg’s measurement uncertainty relation based on statistical distances. Physical review letters, 116(16), 160405. Available at: https://doi.org/10.1103/PhysRevLett.116.160405
12. Huang, S. et. al. (2024). Entropic uncertainty relations for multiple measurements assigned with biased weights. Physical Review Research, 6(1), 013127. Available at: https://doi.org/10.1103/PhysRevResearch.6.013127

Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.