Oct 26 2016
The American Physical Society and the American Institute of Physics this month awarded the 2017 Dannie Heineman Prize for Mathematical Physics to Carl M. Bender of Washington University in St. Louis.
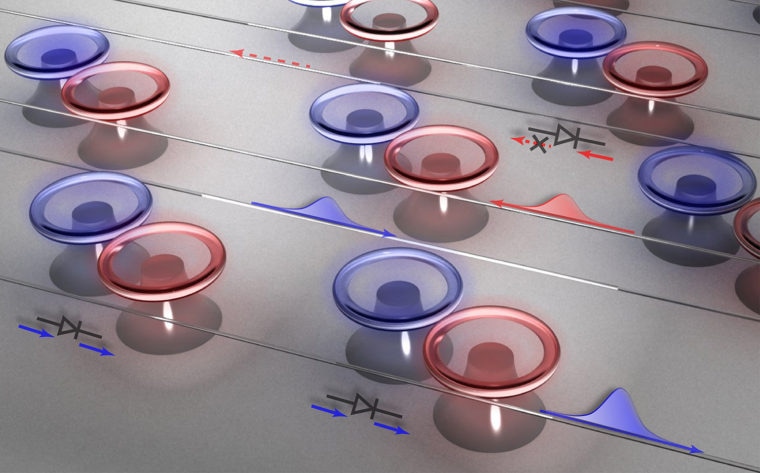 PT symmetry has repeatedly been verified by experiment, including at Bender’s home institution. Coupled optical resonators (paired red and blue toroids on little pedestals) are PT symmetry systems. When they are tuned through a “phase transition” light, instead of moving through them in both directions, can only travel one way. (Photo: Micro/Nano Photonics Laboratory, Department of Electrical & Systems Engineering, Washington University)
PT symmetry has repeatedly been verified by experiment, including at Bender’s home institution. Coupled optical resonators (paired red and blue toroids on little pedestals) are PT symmetry systems. When they are tuned through a “phase transition” light, instead of moving through them in both directions, can only travel one way. (Photo: Micro/Nano Photonics Laboratory, Department of Electrical & Systems Engineering, Washington University)
With this prize he joins the illustrious company of Stephen Hawking, Freeman Dyson, Murray Gell-Mann, Roger Penrose, Steven Weinberg and Edward Witten, among others.
Bender, the Wilfred R. and Ann Lee Konneker Distinguished Professor of Physics in Arts & Sciences, was cited “for developing the theory of PT symmetry in quantum systems and sustained seminal contributions that have generated profound and creative new mathematics, impacted broad areas of experimental physics, and inspired generations of mathematical physicists.”
“I use physics to generate interesting problems, and then I use mathematics to solve those problems,” Bender said. “My approach is to understand what’s going on in the real world — where we live — by studying the complex world, which includes the real world as a special case.”
He explains that everything physicists observe is on the real axis: all the numbers, positive or negative, rational or irrational, that can be found on a number line. But the real axis is just one line in the infinite plane of complex numbers, which includes numbers with “imaginary” parts. “The complex plane helps us to understand what’s going on in the real world,” he said.
How does Bender know which problem to pick, which problems might yield when pushed in this way? “You can smell it,” he said. “Usually something is true because there is a clear argument for why it is true, but if it is true because ‘everybody knows it is true,’ then such a claim is potentially suspect.”
Bender tells a charming story to illustrate what he means. Many years ago his father, a high school physics teacher, put Bender’s son to bed by telling him the story of the brachistochrone, a well-known physics problem that had been solved 300 years before. But, as Bender listened from another room, he realized the accepted version was wrong.
“My father said, ‘This is a classic physics problem; its solution is well known.’ But I said, ‘That’s no longer the right answer.’” Working with an undergraduate eager for a challenge, Bender updated the brachistochrone problem to take into account Einstein’s theory of relativity.
So, Bender listens for physics that produces the dull thunk of an unexamined assumption instead of ringing true, but there is more to it than that. He also is unusually good at seeing moveable patterns: in letters, in chess positions, in musical compositions as well as in mathematical functions.
His presentation slides often include anagrams — he might introduce his name and university as Crab Lender of Washing Nervy Tuitions. He likes to play speed chess and included in his Harvard dissertation a postal chess game that lasted a year and a half. (It was Appendix H, and none of the examiners noticed it.) He also has mastered most of the repertoire for the clarinet and even considered becoming a professional musician.
But theoretical physics isn’t a monologue; it is a conversation. And theoretical physicists, like mathematicians, take ideas for a test drive by describing them to their peers, who help by trying as hard as they can to find flaws.
Because there are only a few hundred highly active mathematical physicists in the world, to have these theory-testing conversations, Bender often travels abroad to conferences or on sabbatical. “The interaction and discussions have enriched my productivity immensely,” he said.
Bender is currently an International Professor of Physics at the University of Heidelberg, Visiting Professor at King’s College London, and Member of the Higgs Center in Edinburgh.
While mathematicians declare success once they’ve convinced other mathematicians of the rigor of their proofs, physicists — while encouraged by the agreement of their peers — are not satisfied until nature also expresses an opinion. They want experimental proof.
And Bender, at heart, is a physicist. “I started out being interested in experimental science and I was good at it,” he said. “Built a lab in my house, built my ham rig, ran a radio repair business, etc. But I think experimental science was too slow for me. I preferred to work with pencil and paper at my own pace.
“Physics is something you ultimately know is right or wrong, and mathematics is always right. So that’s why physics is tricky, more dangerous,” he added.
So “the best thing that ever happened” to Bender was the confirmation by experiment of a daring quantum-mechanical theory he and his former graduate student Stefan Boettcher proposed in 1998.
This is the PT symmetry cited in the Heineman Prize. Characteristically, he arrived at this theory by questioning one of the fundamental assumptions of quantum mechanics.
This axiom states that certain aspects of quantum mechanics must be Hermitian, meaning, among other things, that they must remain in the realm of real numbers. “But insisting that quantum mechanics must be Hermitian,” Bender said, “is like saying all numbers must be even.”
Bender and Boettcher proposed a new non-Hermitian theory, a complex generalization of quantum mechanics, which they called PT-symmetric (parity-time symmetric) quantum mechanics.
Parity is the symmetry operation that turns your left hand into your right. Time reversal just means that time runs backward rather than forward.
In two famous Nobel-winning experiments, other physicists had shown that the universe is neither parity nor time symmetric. A left-handed laboratory can obtain different experimental results from a right-handed laboratory, and a laboratory traveling backward in time can obtain different results from a laboratory traveling forward in time.
What Bender and Boettcher argued is that if you reflect both space and time, everything returns to normal. This is because a parity reflection can be exactly compensated by a time reversal.
Bender and Boetccher also made a prediction based on their theory, so that the theory was falsifiable. The prediction was that PT-symmetric systems can undergo a transition from real to complex energies. PT symmetry would be broken at this transition, and the behavior of the system would change in an interesting — and observable — way.
The neat thing about this was that some optical systems obey equations similar to the quantum-mechanical ones that govern atoms. So PT-symmetric systems can be constructed from simple optical components, such as lasers and optical fibers. “The trick,” Bender said, “is to couple a component with gain, where energy flows into the system, to a component that exhibits loss, where energy flows out of the system.”
The first experiment to confirm the theory was carried out by eight scientists at two universities in the United States and two in Canada, but was physically located at the University of Arkansas. The theory of PT symmetry has since been repeatedly verified by many other experiments.
Bender heard about the first experiment in 2008, nearly 10 years after publishing the theory. Demetrios Christodoulides of the University of Central Florida emailed him to say his group was pretty certain they had seen the PT phase transition. “If everything goes well, with a bit of luck, we may have an experimental explosion in the PT area,” Christodoulides wrote.
“I was on cloud nine for weeks,” Bender said. “It took me a long time to come down because never in my life did I think that I would ever predict anything that was directly observable in a laboratory experiment, not to mention a very simple experiment.”