Repeat-Until-Success Algorithm for Quantum Gate Decomposition

Repeat-Until-Success (RUS) is a technique for performing quantum gate decomposition, which is crucial for enabling the execution of relevant algorithms on quantum computers.

This article will examine Repeat-Until-Success from two distinct perspectives. First, a theoretical analysis of the approach will be outlined before exploring one of its most intriguing future applications: quantum neural networks.

Specifically tailored for superconducting qubits, the example effectively demonstrates real-time feedback concepts that can be easily extended to multi-qubit algorithms.

Introduction

As quantum computing technology advances, there is an increasing demand for efficient algorithms that can translate high-level quantum algorithms into low-level fault-tolerant quantum gates.

Typically, this operation is separated into two steps: choosing a universal gate set and applying a decomposition method to transform an arbitrary quantum circuit into a sequence of gates from the chosen set.

While the choice of the gate set is typically influenced by the properties of the underlying technological platform, the range of possibilities expands considerably when it comes to the decomposition procedure.

An effective decomposition algorithm should minimize the number of gates required to implement the quantum algorithm while ensuring a specified level of accuracy indicated by an approximation error ϵ.

Among the existing decomposition algorithms, this article will focus on Repeat-Until-Success (RUS), which was initially proposed in 2014.¹

RUS is a non-deterministic family of decomposition algorithms that aim to decompose a given gate U using only gates from a specific set. The working principle of RUS involves several common steps shared by many quantum algorithms:

1. The target qubits are initialized in an arbitrary state |ψ⟩ and entangled with additional ancilla qubits in a known state;
2. Gates from the chosen set are applied to the target and ancilla qubits;
3. The state of the ancilla qubits is measured, and subsequent actions are taken based on the measurement outcome.

With an appropriate choice of the applied gates, some of the possible measurement outcomes will correspond to the target qubits being collapsed in the target state U|ψ⟩, which are referred to as success outcomes. Once a success outcome is obtained, the algorithm is considered complete.

Conversely, other outcomes correspond to the target qubits collapsing into an undesired state, known as failure outcomes. In such cases, a recovery operation is applied to reset the qubits to their initial state, and the procedure is repeated until a success outcome is achieved, hence the name "Repeat-Until-Success."

RUS has demonstrated its potency as a valuable tool for quantum computation, finding practical applications in various problem domains. For example, in fault-tolerant quantum computation, RUS can be utilized to implement fault-tolerant gates that require magic state distillation, such as the T gate.

Magic state distillation involves preparing a specific state from multiple qubits in mixed quantum states, and RUS offers an algorithm for its implementation.²

Moreover, research has shown¹ that RUS can decompose any single-qubit unitary using only gates from the universal set {H, T}, significantly reducing the number of necessary T gates compared to other decomposition algorithms, thereby improving performance.

Lastly, RUS also finds applications in the pioneering field of quantum machine learning, particularly in the implementation of quantum neural networks.³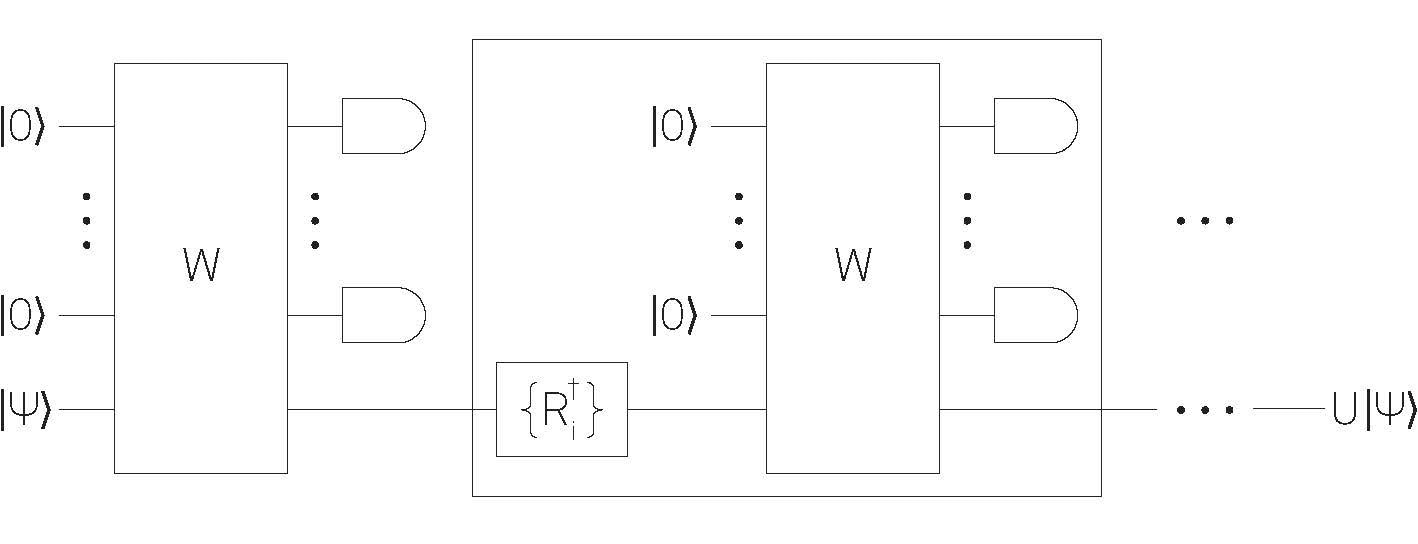

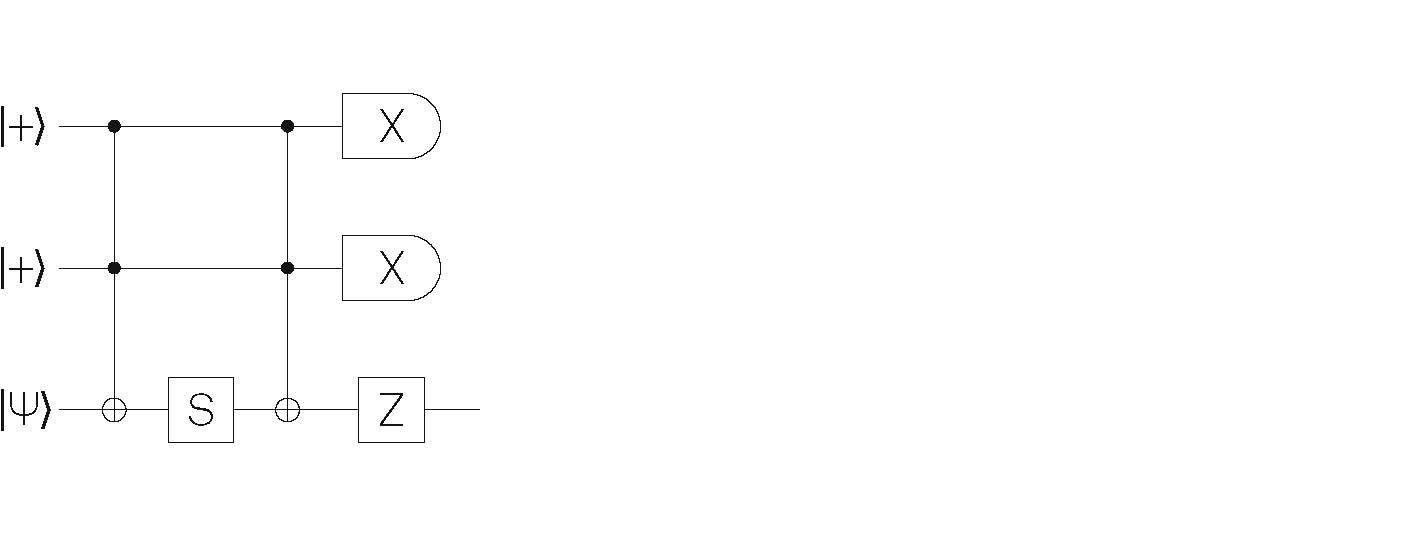
Figure 1. (a) Circuit representation of a typical RUS algorithm. (b) Example of a circuit that can be used in a RUS algorithm. Image Credit: Zurich Instruments AG

This article will now dive deeper into the concept of Repeat-Until-Success algorithms. It will then explore how RUS can be employed to create a quantum neural network, which is one of the most exciting applications of this technique.

Finally, a tabletop demonstration will showcase the implementation of a RUS algorithm on superconducting qubits, incorporating real-time feedback utilizing Zurich Instruments devices.

Concept

Repeat-Until-Success algorithms aim to apply a desired gate U to an arbitrary input state by exclusively utilizing gates from a typically universal set U. The algorithms follow a general structure, as depicted in Figure 1(a):

1. m ancilla qubits are prepared in a predetermined initial state (e.g., |0⟩^⊗m);
2. Given an input state |ψ⟩ on n qubits (called target qubits), a unitary W is applied to all the n+m qubits using gates from U;
3. The ancilla qubits are measured on a computational basis. The resulting output of the circuit represents the state of the n target qubits after measurement, denoted as Φ_i |ψ⟩. Here, Φ_i represents a quantum channel that relies on the measurement outcome i ∈ {0, 1}^m of the ancilla qubits;
4. The measurement outcomes are categorized into two sets: "success" and "failure." In case of a "failure" outcome, a recovery operation is applied to the ancilla and target qubits to revert them to the initial state, and the procedure is repeated. Conversely, if the outcome indicates "success," the output state becomes the desired output U|ψ⟩, and the algorithm finishes.

The example 3-qubit circuit shown in Figure 1(b) illustrates this concept. The circuit employs two ancilla qubits initialized in the state |+⟩, and their measurement results are obtained at the circuit's end. When the measurement outcome is 00, the circuit effectively applies the gate 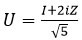to the target qubit's state |ψ⟩.

For any other measurement outcome, the state |ψ⟩ remains unaltered, signifying that the circuit has implemented the identity operation on the target qubit. Consequently, gate U can be implemented using RUS by iteratively executing this circuit until the measurement outcome is 00.

While the 3-qubit example serves didactic purposes, it is of a scale that is not used in practical applications. To gain an understanding of the complexity involved in the application of the RUS concept in such cases, an example specifically designed for quantum machine learning is outlined below.

RUS for Quantum Neural Networks

The implementation of quantum neurons in quantum neural networks can be facilitated by employing the Repeat-Until-Success scheme. Quantum neural networks offer advantages over classical neural networks in terms of faster training and improved generalization of new data.⁴

To understand the principles of operation of quantum neural networks, it is helpful to recollect the notion of classical neural networks, which serve as their inspiration. Neurons are the building blocks of classical neural networks. They are functions that accept n real values x₁, x₂,..., x_n as input and create a single real-valued output.

Both the input and output values are restricted to a specific range, such as [0, 1] or [−1, 1]. For quantum neural networks, the range [−1, 1] is utilized due to its convenience.

A neural network is made up of various layers, each having numerous neurons. The output of neurons in a single layer is transformed into input for neurons in the following layer. The initial layer of neurons receives the problem's input, while the final layer generates a solution to the problem.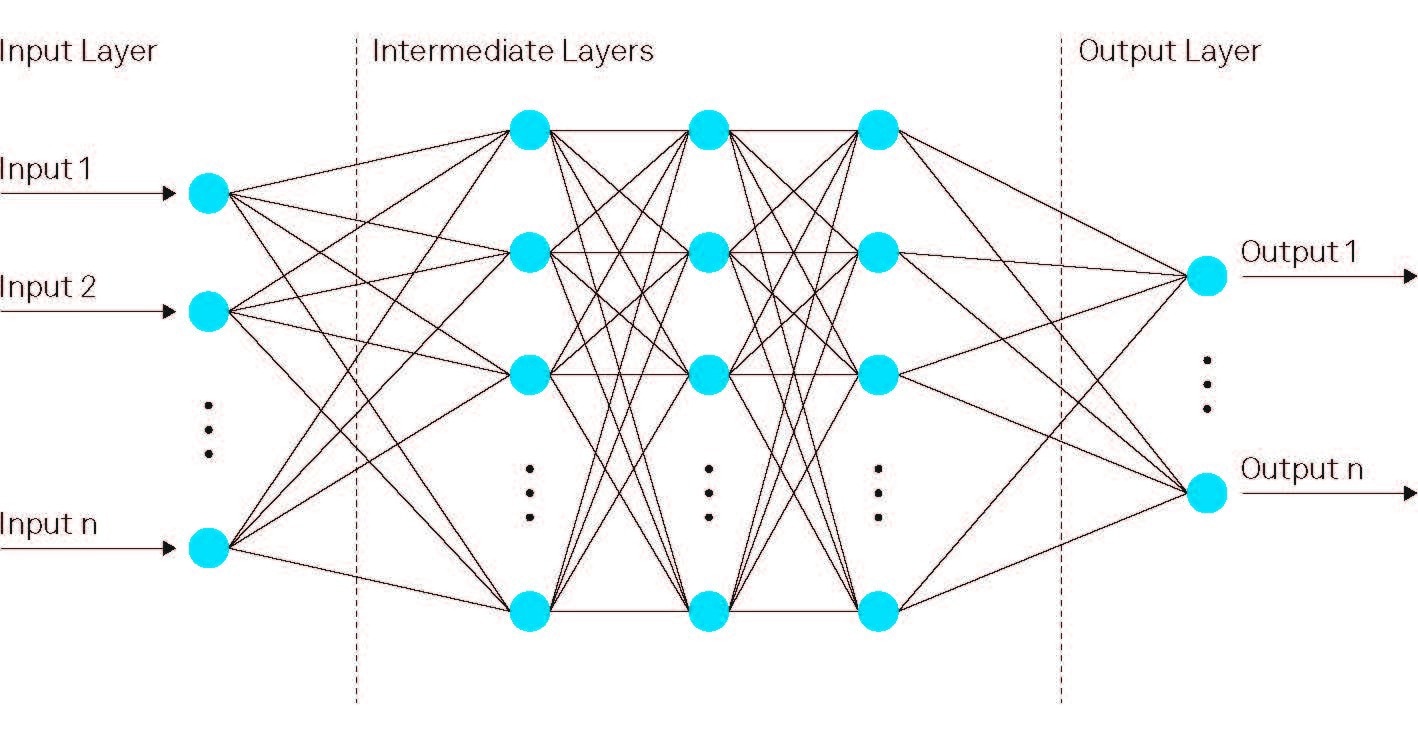

Figure 2. Scheme representing the structure of a neural network. Image Credit: Zurich Instruments AG

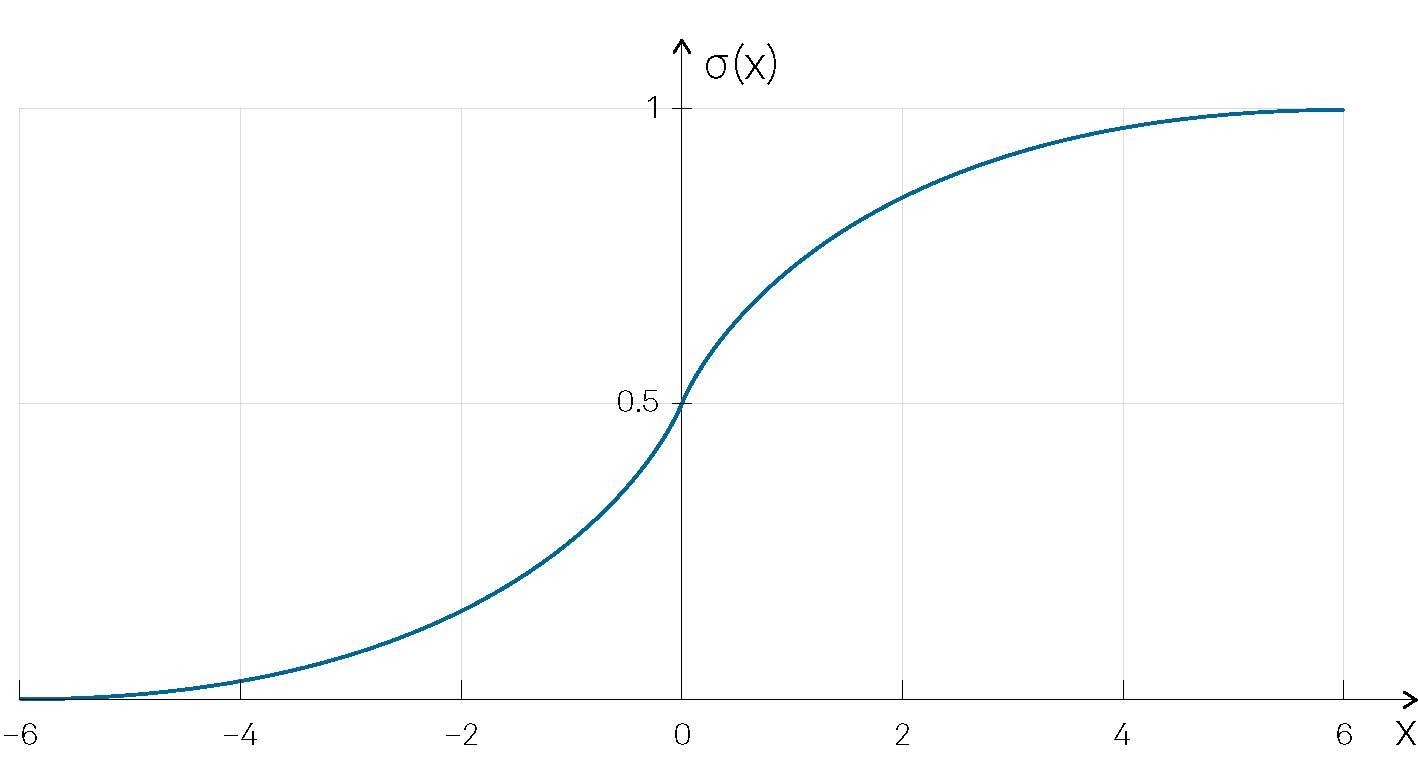
Figure 3. The sigmoid function 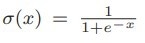 (top) or the hyper-bolic tangent tanh  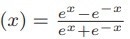 (bottom) are usually chosen as activation functions for neurons. Image Credit: Zurich Instruments AG

The structural arrangement of a neural network is depicted in Figure 2.

To enable the propagation of information across layers and ultimately derive a solution, the internal behavior of neurons is of utmost importance. This involves mapping inputs to outputs. Neurons calculate their output in the following way:

• The inputs x_i are summed with weights w_i and biased by b, obtaining

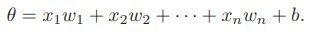
The weights determine the extent of influence each input exerts on the neuron's output, while b represents a constant offset for the weighted sum and establishes the output's order of magnitude.

• The weighted sum θ, which can assume arbitrary values, must be mapped to output within the range [−1, 1]. This is achieved by subjecting θ to a nonlinear activation function, such as the sigmoid or hyperbolic tangent, illustrated in Figure 3. The resulting output, denoted as a, signifies the state of the neuron.

By optimizing the network's parameters, including the weights, bias, and activation function, the neural network can be trained, and the desired solution to a given problem can be obtained. Similar to classical neural networks, quantum neural networks comprise layers of neurons.

However, in the quantum realm, the state of a neuron is associated with a qubit, and its generic quantum state is represented as

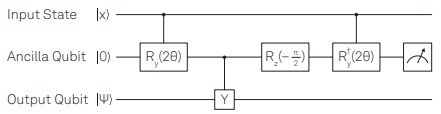
Figure 4. Building block of RUS implementing a quantum neuron. If the ancilla measurement returns 0, the circuit has applied R_y(2q(θ)) on the output qubit, with q(θ) = arctan(tan² (θ)). If the measurement returns 1, the circuit has applied R_y(π/2) onto the output qubit. Image Credit: Zurich Instruments AG

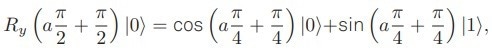
where a ∈ [−1, 1]. For a = −1 and a = 1, the neuron resides in the quantum states |0⟩ and |1⟩, respectively. For intermediate values of a, the neuron exists in a quantum superposition of |0⟩ and |1⟩.

The inputs of the neuron consist of n qubits in the state x⟩ = |x₁⟩|x₂⟩ · · · |x_n⟩. To simulate the classical weighted sum θ = x₁w₁ + · · · + x_nw_n + b, an ancilla qubit initialized in |0⟩ is employed. For each input qubit, a controlled rotation R_y(2w_i) is applied to the ancilla, with the i-th input qubit serving as the control. This corresponds to the application of R_y(2x_iw_i).

Finally, R_y(2b) is applied to the ancilla. Following this procedure, the ancilla qubit assumes the state R_y(2θ)|0⟩.

The last step in preparing the quantum neuron entails performing a rotation R_y(2q(θ)) on the output qubit, where q represents a nonlinear activation function, potentially resembling a sigmoid function. This step can be achieved using a RUS algorithm.

The circuit for this process is depicted in Figure 4. It acts on the output qubit, conditioned by the outcome of the ancilla measurement. If the measurement yields 0, the circuit applies R_y(2q(θ)) to the output qubit, where q(θ) = arctan (tan² (θ)) represents a sigmoid-like function. If the measurement yields 1, the circuit applies R_y(π/2) to the output qubit.

Consequently, RUS can be applied identifying the measurement outcome 0 with "success" and 1 with "failure". In the event of failure, the recovery operation R_y(−π/2) is employed, and the circuit in Figure 4 is re-applied.

Once success occurs, the RUS process concludes, indicating completion. However, there is an opportunity to enhance the activation function's characteristics and establish a more pronounced threshold behavior.

Threshold behavior is the intended state in which the output qubit approaches R_y(π)|0 ⟩ = |1 ⟩ (a = 1) for values of θ greater than π/4, and for values less than π/4, the output qubit approaches R_y(0)|0 ⟩ = |0 ⟩ (a = -1). Based on the value, this modification offers a more exact and noticeable differentiation between the two output states.

This is possible by concatenating multiple runs of the RUS procedure. This means that RUS is run once, repeatedly applying the circuit in Figure 4 and the recovery operation until a success happens.

After that, RUS is run again using the output of the previous run as the starting state for the output qubit. When this procedure is repeated for a total of k times, the rotation R_y(2q^Οk (θ)) is effectively applied to the output qubit.

The function q^Οk (θ) for different values of k is illustrated in Figure 5. As the value of k increases, q^Οk (θ) acquires a stronger threshold behavior, leading to a clearer differentiation between output states based on the value of θ. 

References and Further Reading

1. Adam Paetznick and Krysta M. Svore. Repeat-until-success: Non-deterministic decomposition of single-qubit unitaries. arXiv:1311.1074, 2013.
2. Sergey Bravyi and Alexei Kitaev. Universal quantum computation with ideal clifford gates and noisy ancillas. Physical Review A, 71(2), 2005.
3. Yudong Cao, Gian Giacomo Guerreschi, and Alán Aspuru-Guzik. Quantum neuron: an elementary building block for machine learning on quantum computers. arXiv:1711.11240, 2017.
4. Amira Abbas, David Sutter, Christa Zoufal, Aurelien Lucchi, Alessio Figalli, and Stefan Woerner. The power of quantum neural networks. Nature Computational Science, 1:403, 2021.
5. Elena Acinapura. Jupyter notebook: Repeat-Until-Success algorithm on superconducting qubits.
6. Max Ruckriegel. Multiplexed Readout of Super-conducting Qubits with the UHFQA, 2020.

This information has been sourced, reviewed and adapted from materials provided by Zurich Instruments AG.

For more information on this source, please visit Zurich Instruments AG.