Congestion is a major issue in a variety of settings, including supermarket lines, urban traffic, transportation, local networks, and 5G and LTE-A networks. Congestion issues develop when users compete for a limited number of resources, causing all competitors’ latency to increase. Authors in the journal Quantum Reports have produced a study of many game-theoretic defense techniques for Wireless Sensor Networks.

Study: Mitigation of Routing Congestion on Data Networks: A Quantum Game Theory Approach. Image Credit: diy13/Shutterstock.com
Because the actions of agents (packets on the network or automobiles in a city) adversely influence the overall system performance, congestion issues lend themselves to description using Game Theory.
Several studies on the threat mitigation problem have recently been published in the context of Wireless Sensor Networks (WSN), a form of network that experiences a more demanding environment than standard networks.
In addition, a game theory model based on intelligent drop packet techniques is suggested to reduce congestion in wireless body sensor networks.
Furthermore, researchers now know that by incorporating quantum computing capabilities into game theory models, improved results may be achieved. The authors of this paper consider the Nash equilibria and correlated equilibria of classical and quantum games in terms of Pareto efficiency.
the researchers concentrated their research on three famous games: the prisoner’s dilemma, the battle of the sexes, and the game of chicken, and showed that under quantum mixed Pauli strategies, the Nash equilibria of these games are closer to Pareto optimum solutions than their classical counterparts.
The Braess paradox was investigated together with an examination of the flow in a network with quantum resources - more precisely, networks that deliver quantum entangled particles to the users before they play their strategies, where quantum routing games were originally presented. In addition, in quantum communication networks, a quantum game is used to reduce spectrum allocation times and power usage.
Researchers begin by designing a network that provides both classical and quantum packets and then develops a routing algorithm based on Game Theory formalism. Following that, many variables containing information about the network’s dynamics were monitored, and scientists found that the protocol that employs quantum game theory rules outperformed its classical counterpart substantially.
Researchers propose a decentralized self-organization strategy based on gate-based quantum computers in this paper. Finally, because of the current lack of perfect quantum computers, the impact of noise on our system is investigated. This is accomplished through simulations employing quantum noise models as well as the use of existing IBM noisy quantum computers available on the internet.
Methodology
The main objective is to reduce the overall transmission time, which is calculated by adding the routing and travel times. In this concept, routing time is related to the number of games a packet needs to play before reaching its ultimate path.
Figure 1 is an example of an n1=10 nodes network, with packets traveling across shown in various colors.
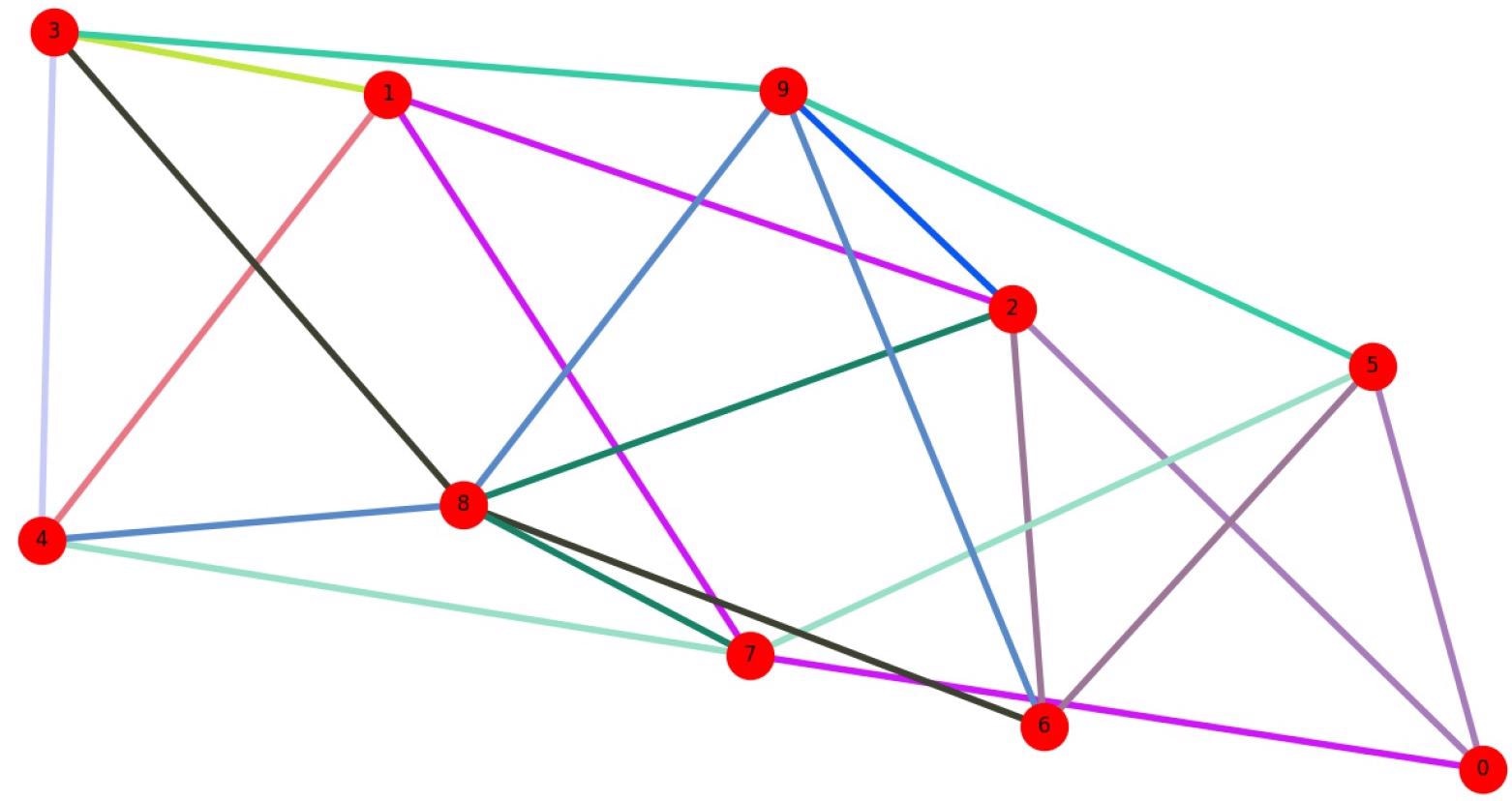
Figure 1. Example of network model for n1=10. Image Credit: Silva, et al., 2022
Table 1 shows an example of a scenario in which two packets are interested in the same channel.
Table 1. Example of two packets interested in the same channel. Source: Silva, et al., 2022
| Players |
|
Player 1 |
| Player 0 |
Actions |
0 |
1 |
| 0 |
Neither of them takes the channel and both go to look for another. |
Player 1 takes the channel and player 0 goes to search another. |
| 1 |
Player 0 takes the channel and player 1 goes to search another. |
Both take the channel creating a congested path. |
Experts use the EWL technique for two players and then extend it for N players to analyze the quantum game for channel choosing. This is accomplished by using the entangling operator 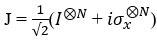 , as shown in Figure 2, with N = 2 players.
, as shown in Figure 2, with N = 2 players.
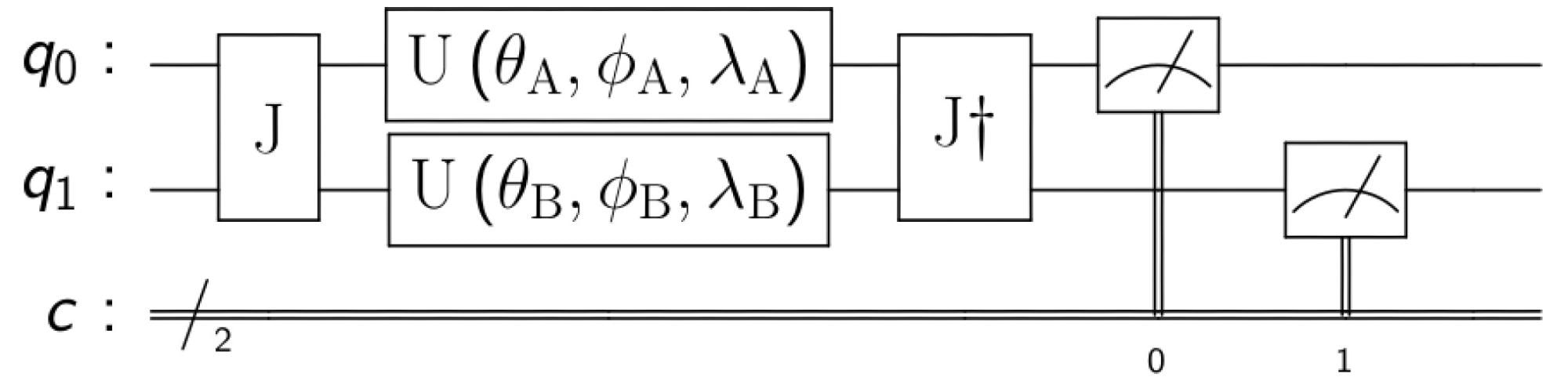
Figure 2. EWL game model for 2 players. Where q0 and q1 are the initial quantum states of the players and c is a classical register where the qubits measurements are stored. Image Credit: Silva, et al., 2022
Results
The results of classical and quantum procedures are compared. The simulations were carried out by averaging the results of 50 distinct auto-generated random network topologies. In each example, the possibility of Pareto optimality and Nash equilibrium is explored. The quantum protocol is further examined under less-than-ideal conditions by simulating a noisy channel and utilizing IBM’s quantum devices.
Figure 3 shows simulations of the traditional game, in which all players have the probability p.
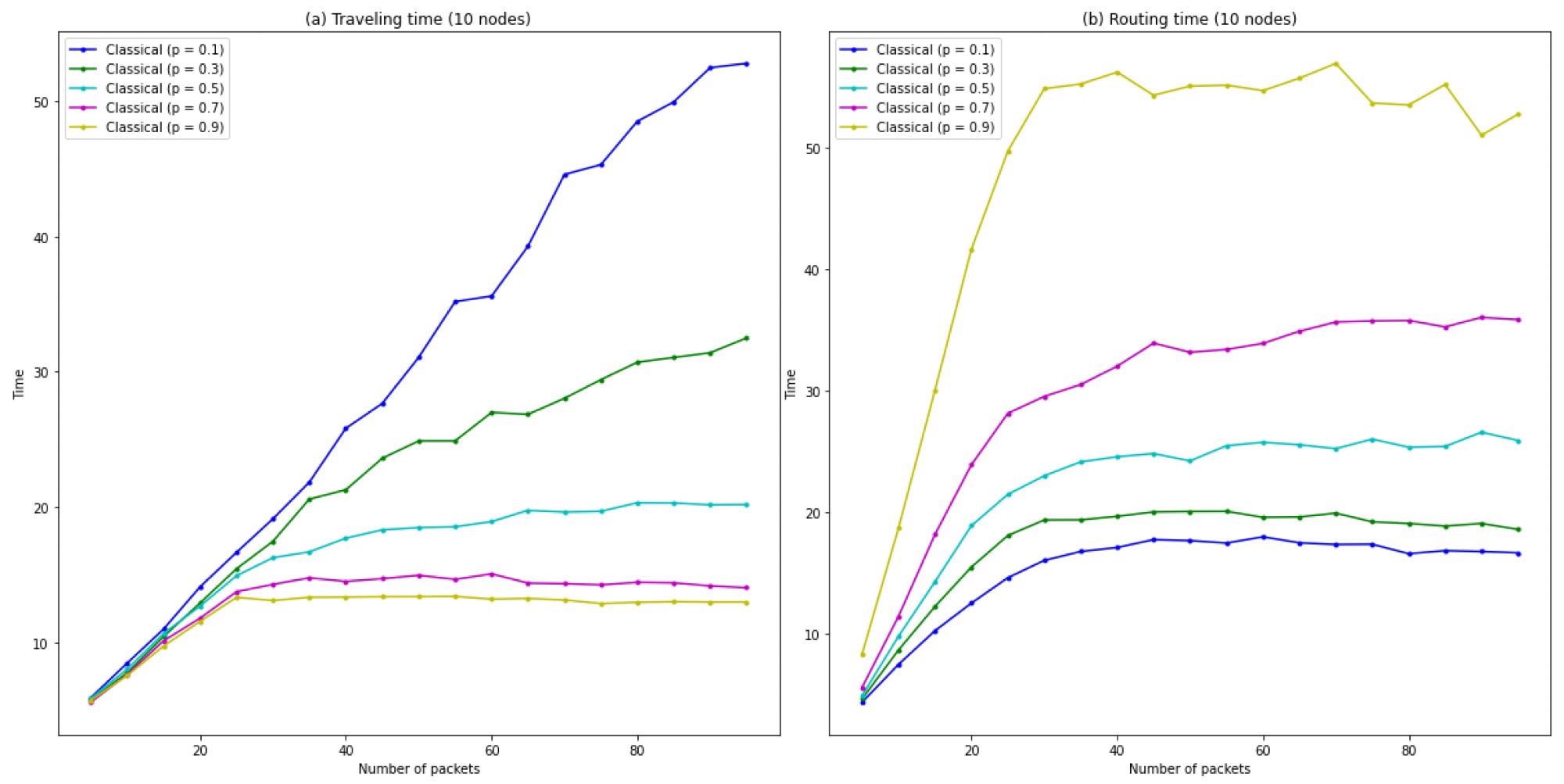
Figure 3. Graphs for different probabilities p of: (a) Traveling time as a function of the number of packets. (b) Routing time as a function of the number of packets. Image Credit: Silva, et al., 2022
This impact may be observed in Figure 4, which depicts travel and routing times for various probability p. When the system reaches a steady state with a large number of packets (n2=100), these findings are achieved.
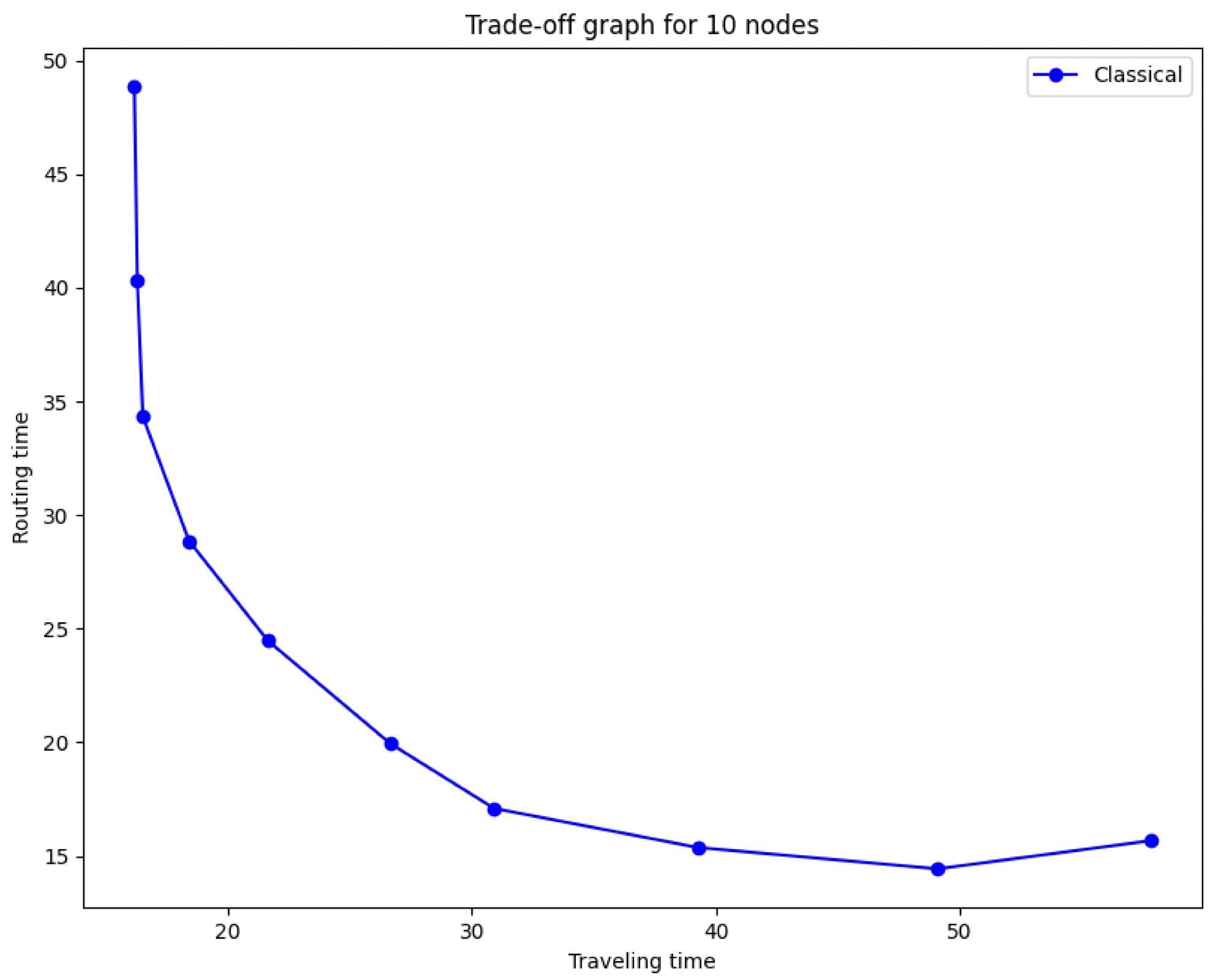
Figure 4. Trade-off between traveling and routing time for different p values between 0 and 0.9. Values of p closer to 0 give a high traveling time and low routing time. Values of p closer to 1 give a low traveling time and high routing time. Image Credit: Silva, et al., 2022
As a result, each player must select three angles, which researchers will refer to as φX, φY, and φZ. As illustrated in Figure 5, researchers suggest the strategy 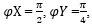 and φZ= 0 for each player in the design.
and φZ= 0 for each player in the design.
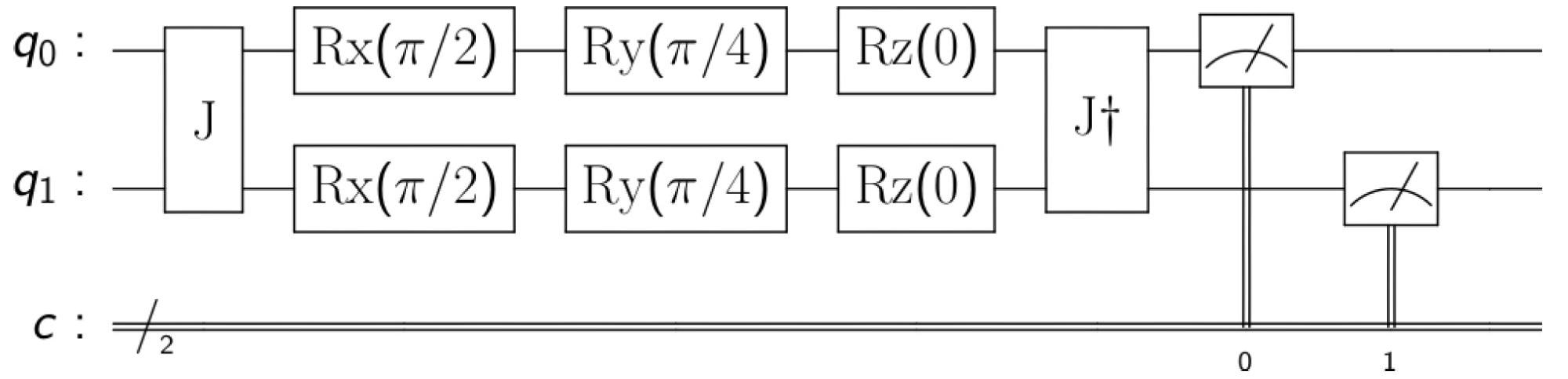
Figure 5. Game model for 2 players. Image Credit: Silva, et al., 2022
Figure 6(a, b) compares the quantum protocol performance when all users use 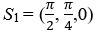 in the classical protocol performance.
in the classical protocol performance.
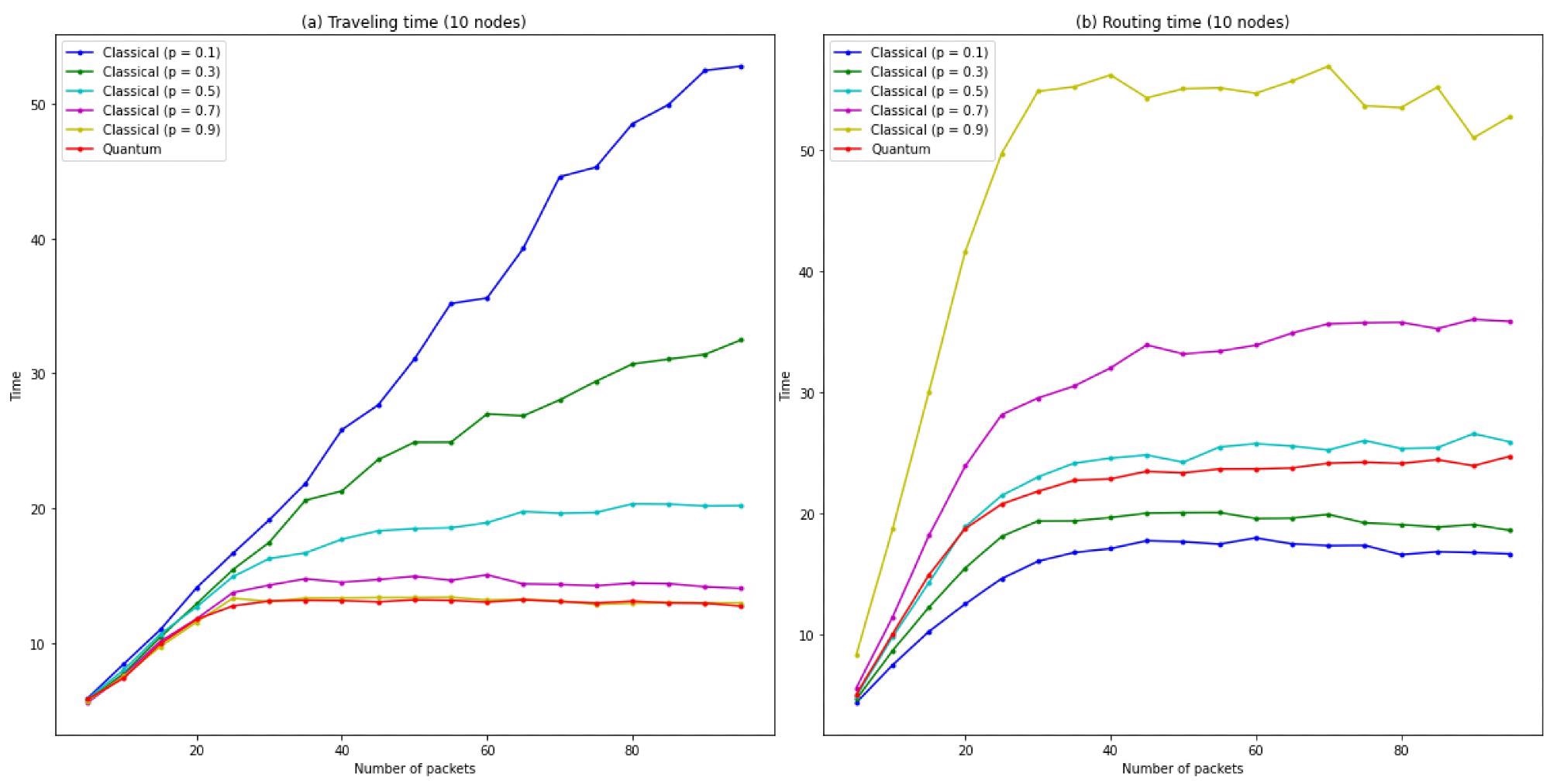
Figure 6. Graphs for different probabilities p and the quantum case: (a) Traveling time as a function of the number of packets. (b) Routing time as a function of the number of packets. Image Credit: Silva, et al., 2022
As a result, experts can see in Figure 7 how this quantum protocol overcomes the classical traveling-routing time trade-off barrier.
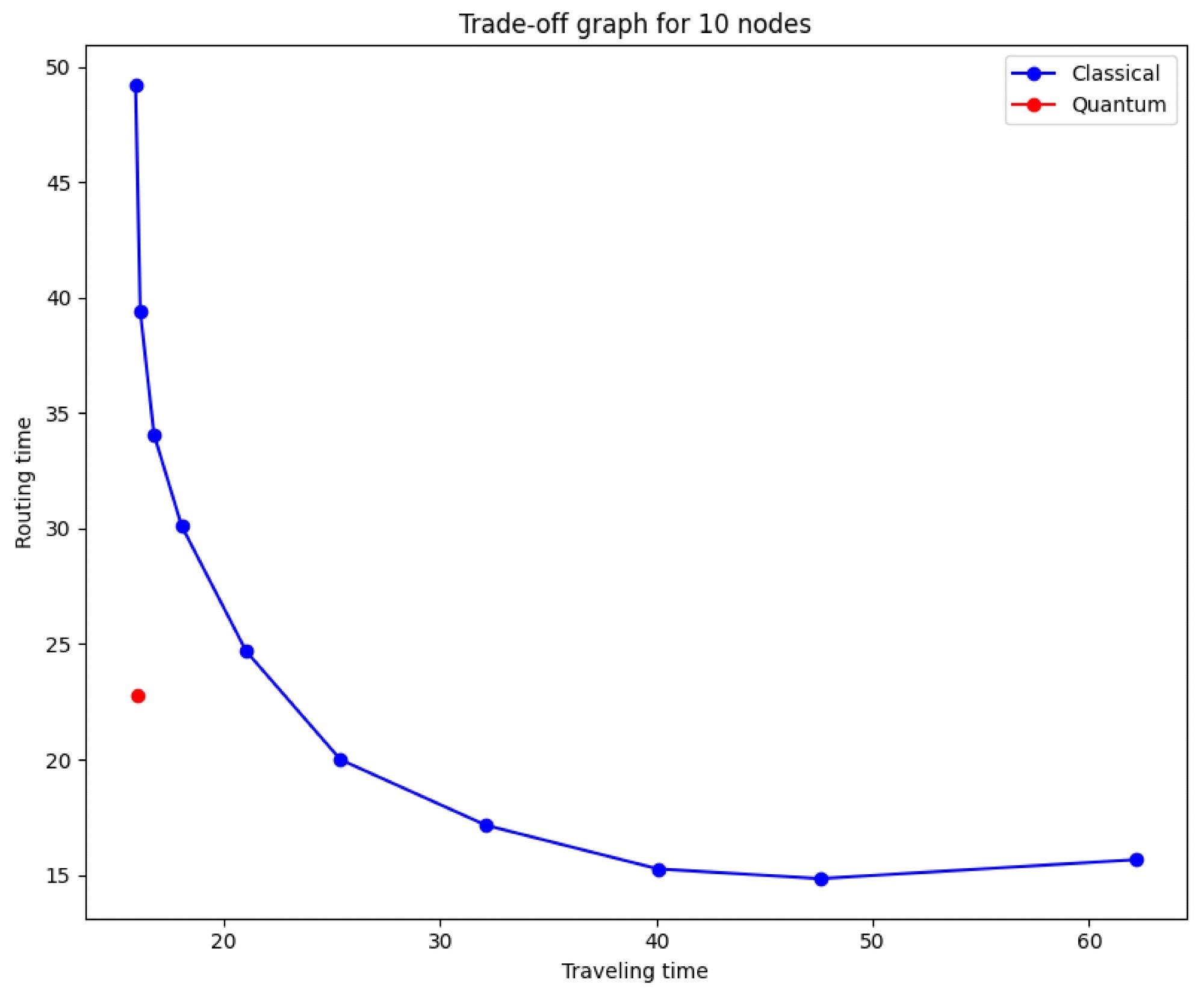
Figure 7. Trade-off barrier broken by quantum protocol. In red the quantum strategy, in blue different mixed classical strategies with p values between 0 and 0.9. Image Credit: Silva, et al., 2022
When the total time is measured, it is evident that the quantum protocol outperforms the conventional protocol as the number of packets grows and the network gets progressively congested (see Figure 8).
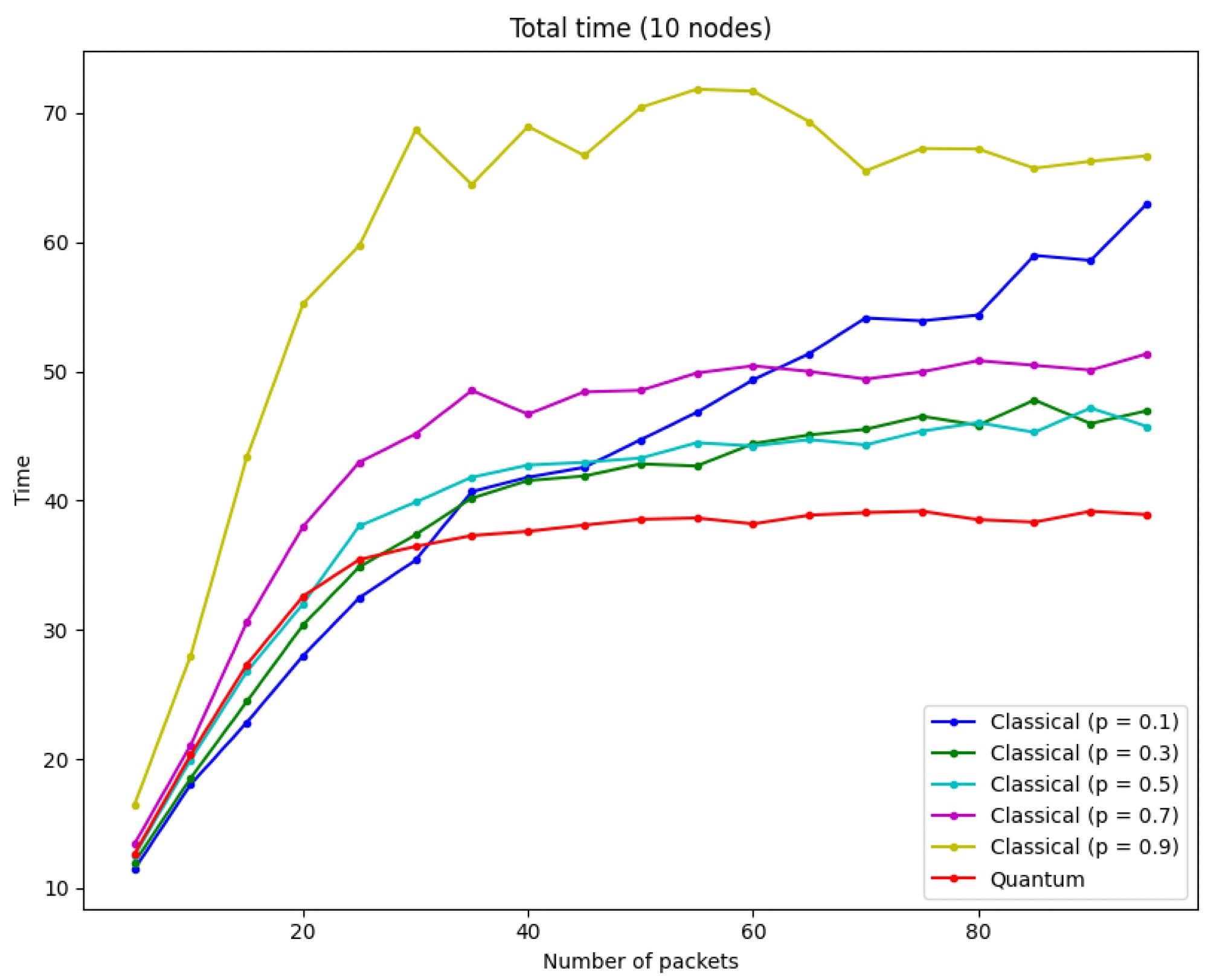
Figure 8. Total time = routing time + traveling time, it is evident that the minimum total time correspond to the quantum case when the number of packets increases. Image Credit: Silva, et al., 2022
Figure 9 illustrates the performance of various quantum techniques.
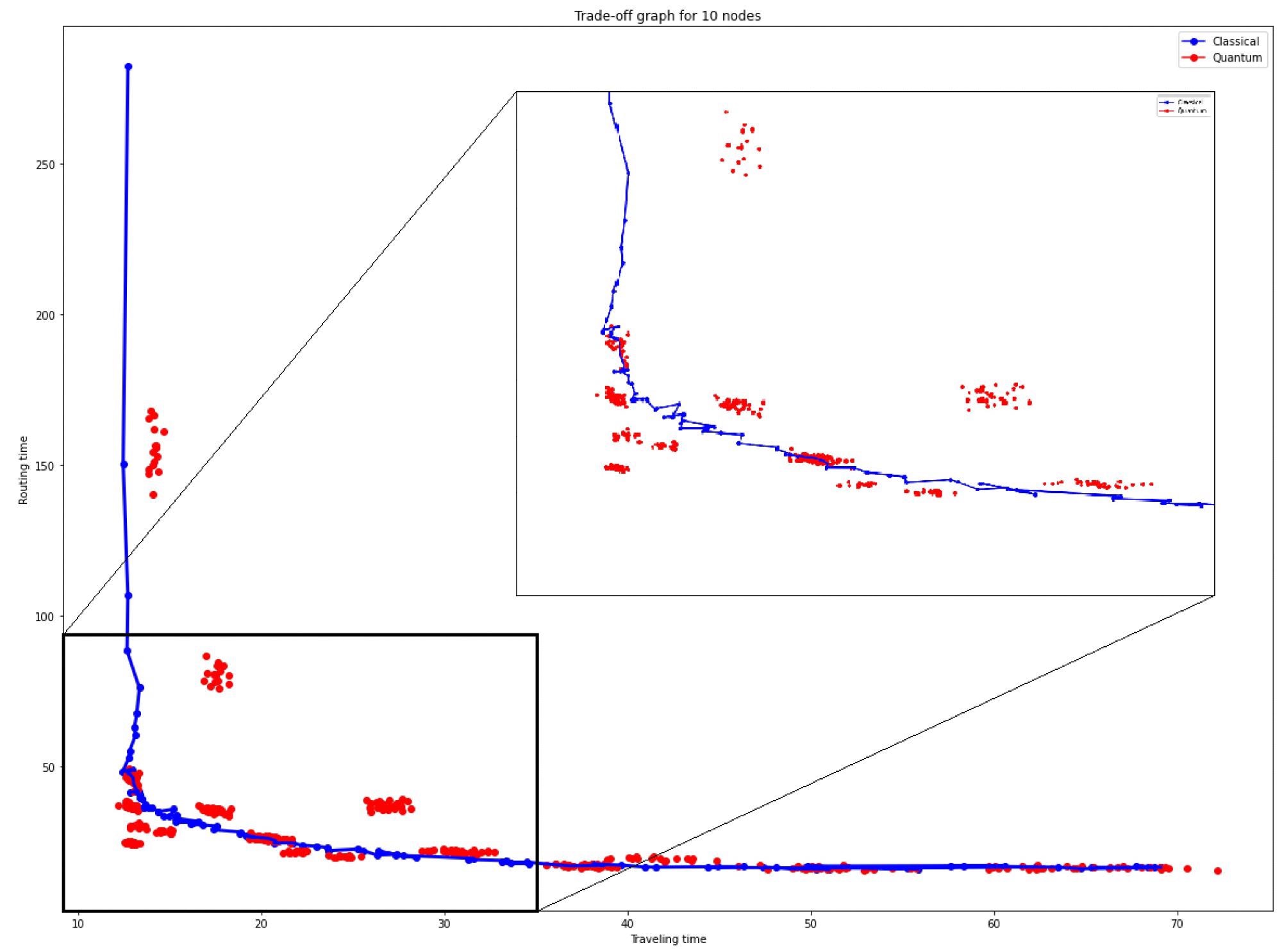
Figure 9. Trade-off barrier broken by quantum protocol. In red different pure quantum strategies, in blue different mixed classical strategies with p values between 0 and 0.99. Image Credit: Silva, et al., 2022
Researchers have been examining the system without taking into account quantum state noise and decoherence. The effects of quantum noise on the system are discussed in this section.
Figure 10 shows the system’s performance for a Pareto optimum situation and various values of C 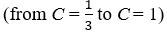 while maintaining the constraint of total positivity.
while maintaining the constraint of total positivity.
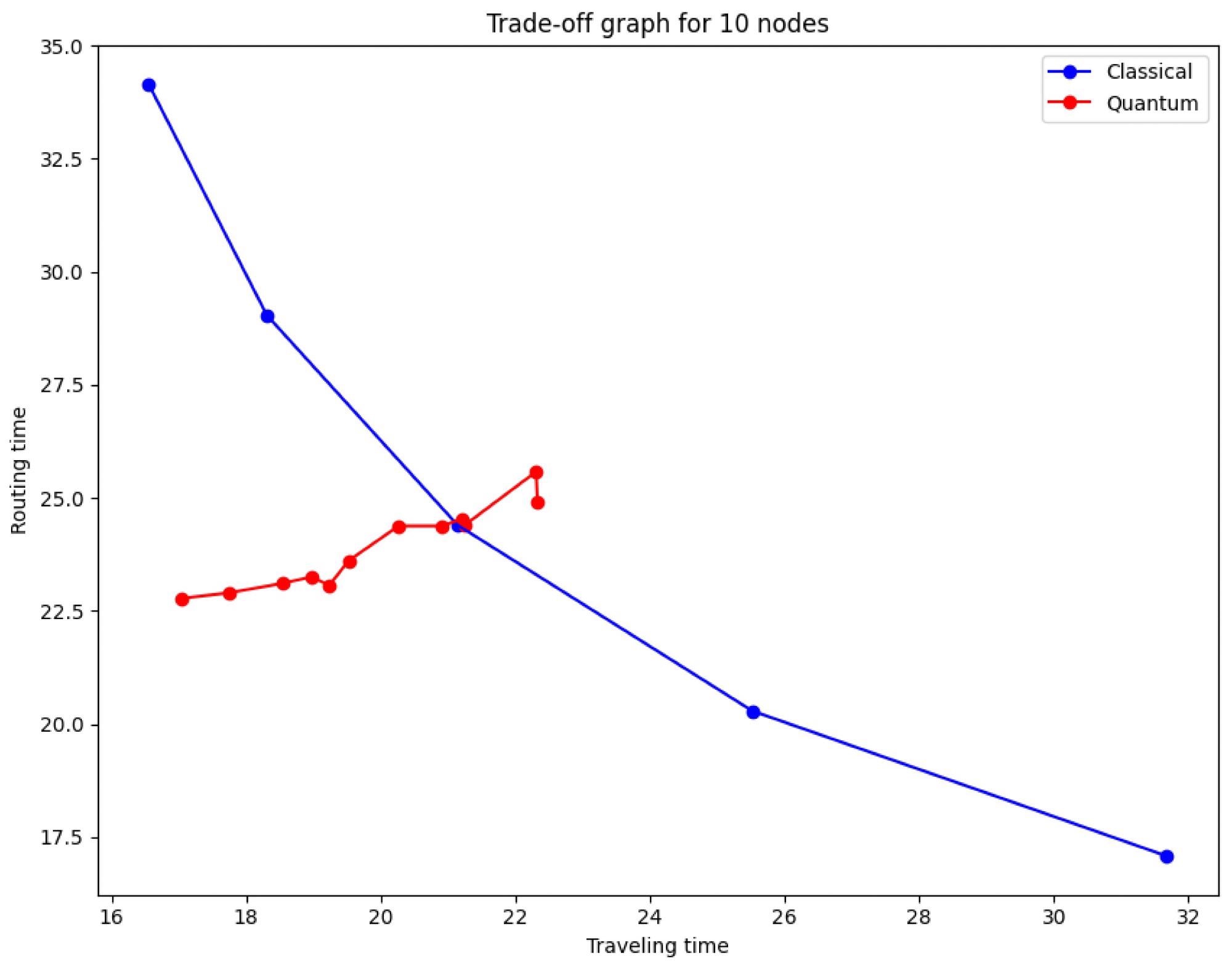
Figure 10. Effect of decoherence in the trade-off barrier by quantum protocol. As the value of C moves away from C=1 (ideal case), the quantum case looks more and more like the classical case. p values between 0.3 and 0.7. Image Credit: Silva, et al., 2022
Because quantum processors in the NISQ era are not smart enough to conduct quantum error correction on a continuous basis, it is critical to evaluate our approach in these types of quantum devices. Figure 11 depicts the final results.
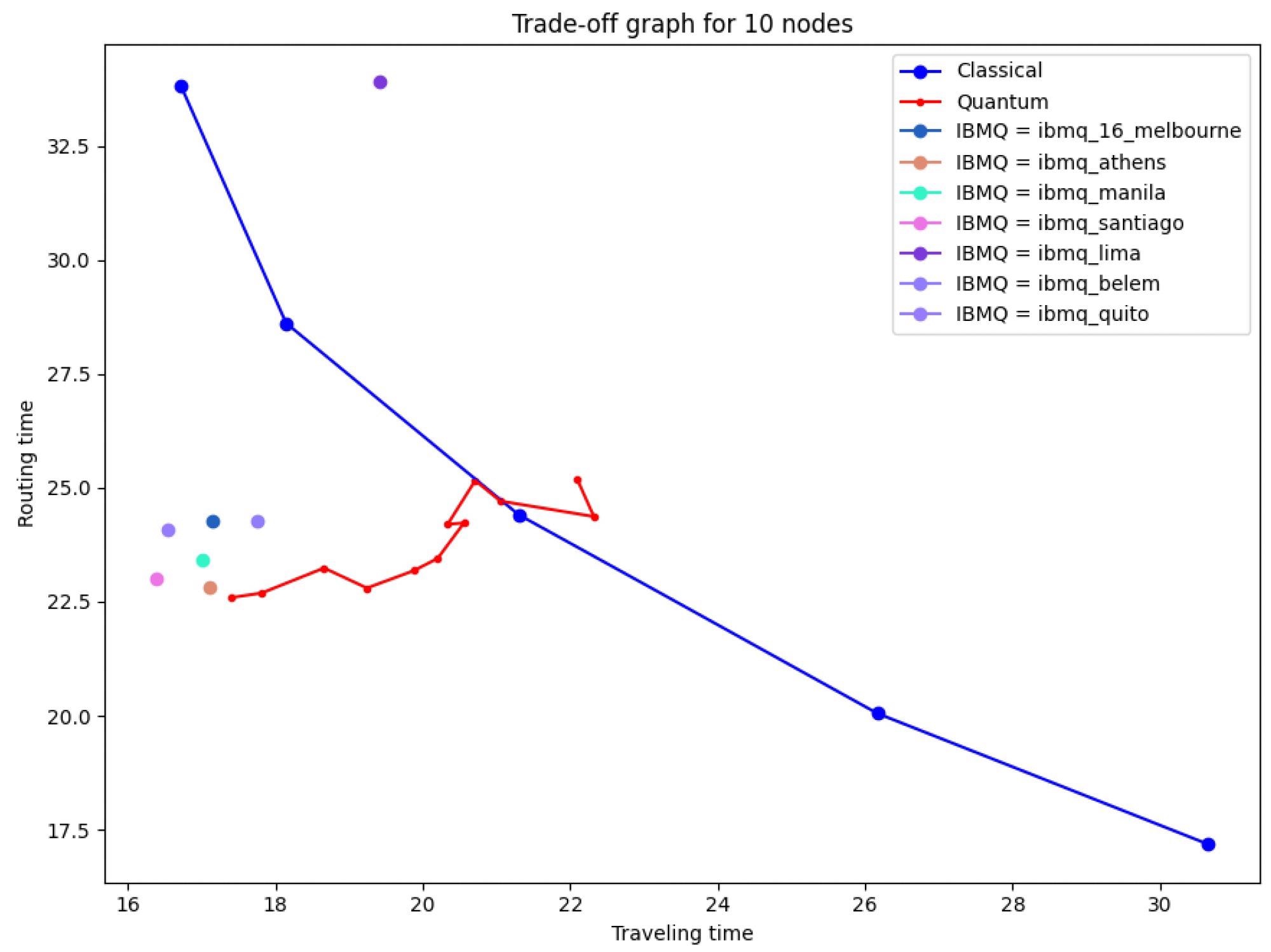
Figure 11. Effect of real devices in the trade-off barrier by quantum protocol. Congestion can be mitigated by making use of IBM NISQ quantum computers. p values between 0.3 and 0.7. Image Credit: Silva, et al., 2022
Conclusion
This paper proposes classical and quantum network protocols based on game theory in order to improve the performance of communication networks. Classical gaming protocols impose a routing and travel time limitation, lowering network performance as the number of packets increases.
Quantum strategies, as provided by the EWL protocol of quantum games, are used to create the quantum model. A three-parameter one-qubit quantum gate model is used to illustrate quantum strategies. Then, as the game progresses from classical to quantum, the players’ strategies are expanded.
Many quantum game techniques overcome the trade-off barrier between routing and travel time found in the standard probabilistic protocol, resulting in improved network performance with rising packet quantity. Nash equilibrium is linked to the stability of quantum techniques. Mixed strategies have been investigated since pure quantum methods are not Nash equilibrium.
In this method, a mixed strategy was demonstrated that is Pareto optimum and seems to be Nash equilibrium. It was also demonstrated that the quantum protocol advantages are still there under the effect of simulated noise and genuine quantum devices.
Researchers have demonstrated that applying a quantum game formalism to a communication network improves its efficiency while managing congestion issues. As a result, making use of quantum computing’s capabilities might open up a whole new world of possibilities in these sorts of complicated systems. Furthermore, scientists may provide solutions that result in significantly more efficient systems.
Journal Reference
Silva, A., Zabaleta, O.G. and Arizmendi, C.M. (2022) Mitigation of Routing Congestion on Data Networks: A Quantum Game Theory Approach. Quantum Reports, 4(2), pp.135-147. Available Online: https://www.mdpi.com/2624-960X/4/2/10/htm
References and Further Reading
- Niyato, D & Hossain, E (2008) Modeling user churning behavior in wireless networks using evolutionary game theory. In Proceedings of the 2008 IEEE Wireless Communications and Networking Conference, Las Vegas, NV, USA, 31 March–3 April; pp. 2793–2797.
- Morgenstern, O & Von Neumann, J (1953) Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA.
- Nash, J F (1950) Equilibrium points in n-person games. Proceedings of the National Academy of Sciences, 36, pp. 48–49. doi.org/10.1073/pnas.36.1.48.
- Abdalzaher, M.S., et al. (2016) Game theory meets wireless sensor networks security requirements and threats mitigation: A survey. Sensors, 16, p. 1003. doi.org/10.3390/s16071003.
- Xu, Q.Y., et al. (2019) An intelligent packet drop mechanism in wireless body sensor network for multiple class services based on congestion control. Procedia Computer Science, 154, pp. 453–459. doi.org/10.1016/j.procs.2019.06.064.
- Abdalzaher, M.S., et al. (2017) sing repeated game for maximizing high priority data trustworthiness in wireless sensor networks. In Proceedings of the 2017 IEEE Symposium on Computers and Communications (ISCC), Heraklion, Greece, 3–6 July; pp. 552–557.
- Meyer, D A (1999) Quantum strategies. Physical Review Letters, 82, p. 1052. doi.org/10.1103/PhysRevLett.82.1052.
- Eisert, J., et al. (1999) Quantum games and quantum strategies. Physical Review Letters, 83, p. 3077. doi.org/10.1103/PhysRevLett.83.3077.
- Szopa, M (2021) Efficiency of classical and quantum games equilibria. Entropy, 23, p. 506.
- Solmeyer, N., et al. (2018) Quantum routing games. Journal of Physics A: Mathematical and Theoretical, 51, p. 455304. doi.org/10.1088/1751-8121/aae31f.
- Zabaleta, O.G., et al. (2017) Quantum game application to spectrum scarcity problems. Physica A: Statistical Mechanics and its Applications, 466, pp. 455–461. doi.org/10.1016/j.physa.2016.09.054.
- Bassoli, R., et al. (2021) Quantum Communication Networks; Springer: Berlin/Heidelberg, Germany, 2021; 23.
- Khan, F.S., et al. (2018) A review of the history, current state, and interpretation. Quantum Information Processing, 17, pp. 1–42. doi.org/10.1007/s11128-018-2082-8.
- Neukart, F., et al. (2017) Traffic flow optimization using a quantum annealer. Frontiers in ICT, 4, p. 29. doi.org/10.3389/fict.2017.00029.
- Yarkoni, S., et al. (2019) Volkswagen and quantum computing: An industrial perspective. Digitale Welt, 3, pp. 34–37. doi.org/10.1007/s42354-019-0166-y.
- Yarkoni, S., et al. (2020) Traffic navigation with quantum computing. In Proceedings of the 1st ACM SIGSOFT International Workshop on Architectures and Paradigms for Engineering Quantum Software, Virtual, 13 November; pp. 22–30.
- IBM Quantum Experience (2021) Available at: https://research.ibm.com/
- Gilbert, E N (1959) Random graphs. Annals of Mathematical Statistics, 30, pp. 1141–1144. doi.org/10.1214/aoms/1177706098.
- Jabbarpour, M.R., et al. (2018) Applications of computational intelligence in vehicle traffic congestion problem: A survey. Soft Computing, 22, pp. 2299–2320. doi.org/10.1007/s00500-017-2492-z.
- Ding, R., et al. (2020) Packet routing against network congestion: A deep multi-agent reinforcement learning approach. In Proceedings of the 2020 International Conference on Computing, Networking and Communications (ICNC), Big Island, HI, USA, 17–20 February; pp. 932–937.
- Benjamin, S C & Hayden, P M (2001) Multiplayer quantum games. Physical Review A, 64, p. 030301. doi.org/10.1103/PhysRevA.64.030301.
- Nielsen, M A & Chuang, I (2000) Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK.
- Ikeda, K & Aoki, S (2021) Infinitely repeated quantum games and strategic efficiency. Quantum Information Processing, 20, pp. 1–24. doi.org/10.1007/s11128-021-03295-7.
- Preskill, J (2018) Quantum Computing in the NISQ era and beyond. Quantum, 2, p. 79. doi.org/10.22331/q-2018-08-06-79