The Heisenberg uncertainty principle is one of the most infamous results in physics, that highlights the difference between the quantum world and the world we inhabit.
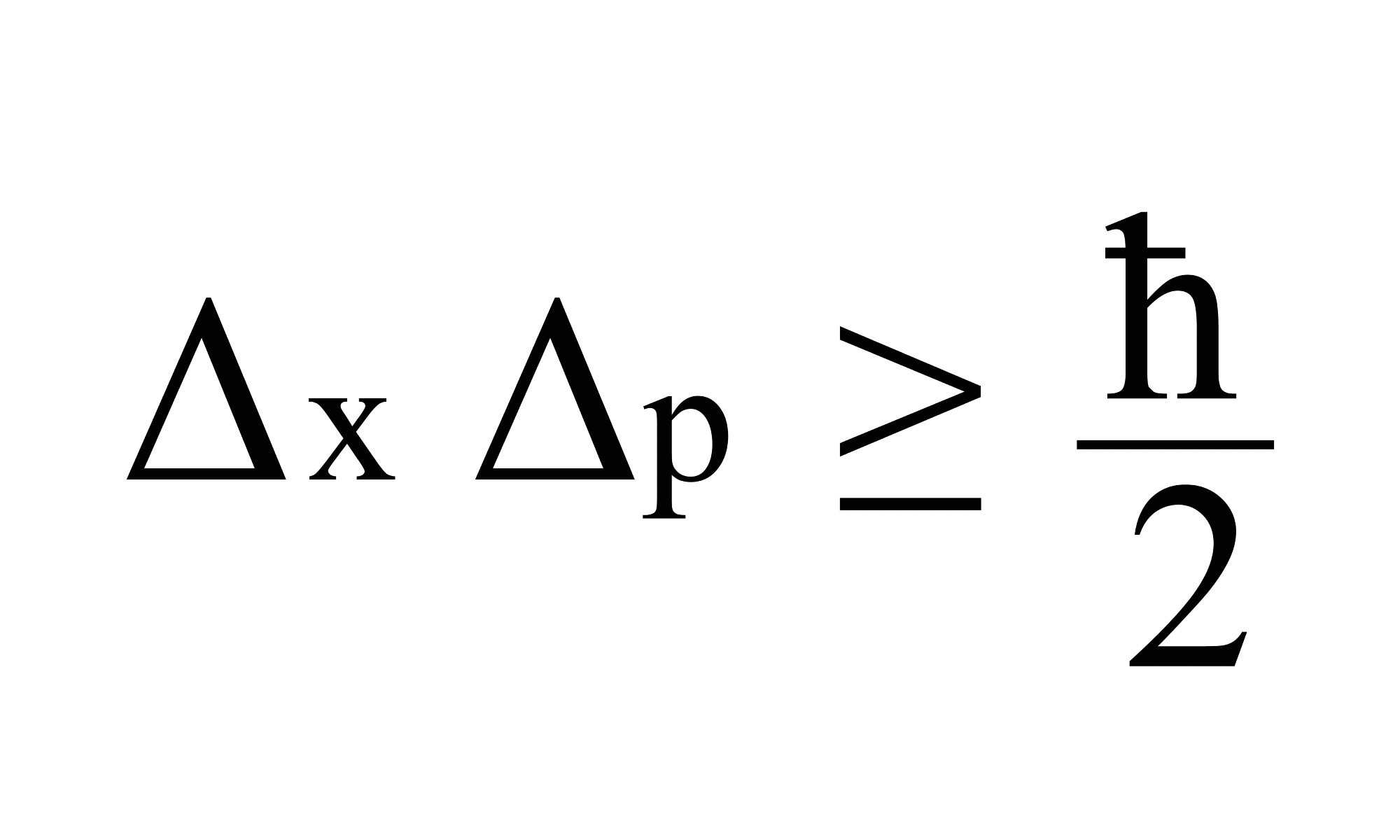
Image Credit: zizou7/Shutterstock.com
A particle physicist is speeding down the highway when she gets pulled over by a police officer. The cop says: “Ma’am, do you have any idea of how fast you were going?”
The physicist replies: “No, but I know exactly where I am.”
This joke is an example of how one of physics’ most famous concepts has made its way into the cultural subconscious. Heisenberg’s uncertainty principle, alternatively just the uncertainty principle, is the idea that in quantum systems, the more precisely you know one quantity, or “observable,” the less precisely you can know another.
First introduced in 1927 by Werner Heisenberg towards the end of a period of discoveries that would reveal the complexities of the microscopic world, separating it from the physics of the macroscopic world, the uncertainty principle is one of the most celebrated results in all of physics.
The most commonly expressed form of this rule is the better you know a quantum system’s momentum, the less well you can know its position, and vice versa.
One of the most important things to remember about this principle is the fact that it has absolutely nothing to do with the precision of our measuring methods or tools. This isn’t a measurement uncertainty—Heisenberg’s uncertainty principle is deeper than this.
Nor should the uncertainty principle be confused with the observer or experimenter effect. This states that the act of attempting to measure the observables of a system changes the state of this system. You could limit this with more careful measurement or with some clever workaround, but Heisenberg’s uncertainty principle is something that cannot be avoided with added care—it is intrinsic to nature.
This leads to some interesting questions, including why we don’t see the uncertainty principle operating in the world around us if it is part of the physics at the heart of the matter.
In other words, the particle physicist in our example would never escape a ticket if the officer who pulled her over knew anything about quantum mechanics. To assess why this is the case, it is useful to first see from where this intrinsic and important aspect of nature arises.
Where Does the Uncertainty Principle Come From?
While the uncertainty principle also applies to quantum characteristics like time and energy, the easiest way to explain it is to tackle the variation of the principle that is first encountered by physics students: momentum and position.
The most generalized version of Heisenberg’s uncertainty principle says that if you measure the momentum of a particle with uncertainty Δp, then you are limited in how precisely you can ‘know’ its position Δx. You can’t know it any more precisely than Δx ≥ ℏ/2Δp, where ℏ (or H-bar) is a value known as the reduced Planck’s constant. Rearranged this gives the uncertainty principle equation for momentum and position, ΔxΔp≥ ℏ/2.
To consider what this implies, we can perform a simple thought experiment, first in the everyday realm of classical physics, then in the microscopic domain of quantum physics.
We take a “classical ball” for which we know its mass precisely. We toss it in the air with a precise velocity. This means we can map its precise trajectory, determine where it will land, and crucially the point where its kinetic energy will have transformed fully into gravitational potential energy, and its ascent will stop.
For a split second, it halts in the air. Then it falls, gradually exchanging its potential energy for kinetic energy. The region beyond which it could travel with the kinetic energy it has is known as the “classically forbidden region.”
What is the Heisenberg Uncertainty Principle? - Chad Orzel
Video Credit: TED-Ed/Shutterstock.com
Now we turn to our “quantum mechanical ball” again; we know precisely its mass and the velocity at which it travels, and thus its momentum when we throw it into the air.
This time the Heisenberg uncertainty principle tells us that we must consider there to be a finite possibility that the quantum ball will continue to travel after its peak.
This is because we are forbidden to know precisely where the ball will stop for that split second when its kinetic energy is exhausted. Thus, there’s a probability of finding our quantum ball in a region that is classically forbidden.
The reason for this difference is that in quantum mechanics a traveling particle — or a quantum ball should such a thing exist — is described by a wave. The wavelength of that wave is associated with the particle’s momentum, while the location of each peak is associated with the probability of finding the particle in a particular location.
So, while you have an infinitely long wave, we know the momentum precisely. However, this leaves us with an infinite amount of peaks, each corresponding to the possibility of finding a particle in a particular location. Thus, though we know the momentum of the particle precisely, we have no clue about its location.
If we want to locate the particle what we need to do is start overlaying the wavelengths. As we do this, what we get are enhanced peaks where each wave’s peaks meet and flat regions where a peak meets a trough, and they cancel each other out. Overlay enough waves, and we get a flat line with one single peak. We now have a definite location for the particle, but what we have done is completely destroy the aspect of the wave that represents momentum.
This forces physicists to completely abandon the concept of trajectory, something that makes it clear just how different the quantum world is from the macroscopic world we inhabit.
Why the Uncertainty Principle Doesn’t Explain Your Lost Keys
The reason that the uncertainty principle applies to the quantum world but not the world of cars, cops, and particle physicists, hinges on a crucial element of the equation that governs it.
The element is ℏ (or H-bar) formally known as the reduced Planck’s constant. It is the result of this constant and how small it is that Heisenberg’s uncertainty principle doesn’t explain why you can never find your keys.
The key is the very small value of the reduced Planck’s constant (ℏ). This means that the lower limit in the uncertainty of measuring the position and momentum of large objects is negligible when compared to massive objects like tennis balls, skipping ropes, or cars.
All matter, not just quantum particles, has an associated de Broglie wave (λdb). For the uncertainty principle to sow a considerable or measurable effect on an object but that wave has to be a comparable size to the Planck’s reduced constant. The de Broglie wave of a ball or a car or your keys is way too small to be subject to the uncertainty principle in any significant way.
That’s why, while revealing the intrinsic and hidden nature of the cosmos at the smallest scales and changing physics forever, Werner Heisenberg still never helped anyone escape a speeding ticket.
References and Further Reading:
Griffiths. D. J, ‘Introduction to Quantum Mechanics,’ Cambridge University Press, [2017].
Feynman. R, Leighton. R. B, Sands. M, ‘The Feynman Lectures on Physics. Volume III: Quantum Mechanics,’ California Institute of Technology, [1965].
Bolton. J, Lambourne. R, ‘Wave Mechanics,’ The Open University, [2007].
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.