In an article recently published in the journal Communications Physics, researchers investigated the feasibility of calculating high-accuracy, finite-size effect-free hyperfine tensors using an improved integration method for the case of the nitrogen-vacancy (NV) center in diamond.
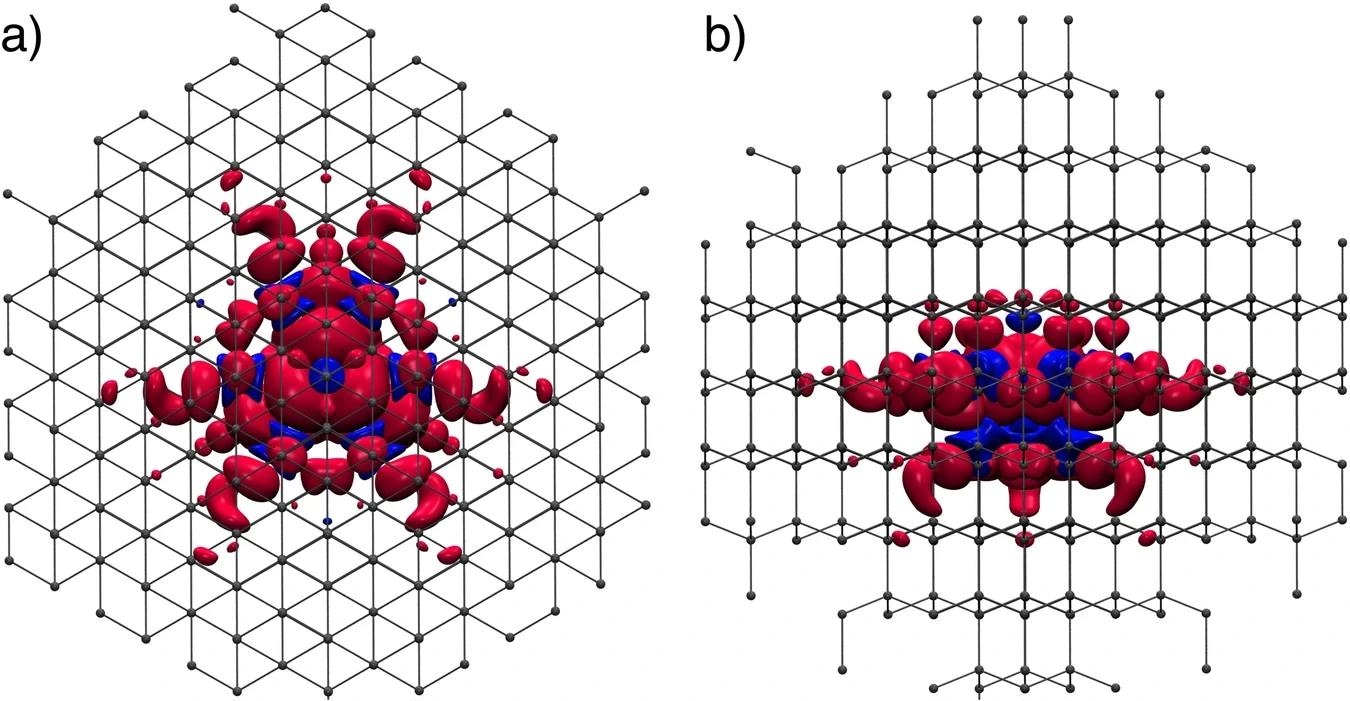 a and b depict top and side views, respectively. Red (blue) lobs indicate positive (negative) spin density isosurfaces and gray dots and bars show the lattice of the diamond. The isosurface value is set to ± 0.003. The blue lobs indicate weak antiferromagnetic couplings with neighboring atoms, e.g., the nitrogen of the NV center. Image Credit: https://www.nature.com/articles/s42005-024-01668-9
a and b depict top and side views, respectively. Red (blue) lobs indicate positive (negative) spin density isosurfaces and gray dots and bars show the lattice of the diamond. The isosurface value is set to ± 0.003. The blue lobs indicate weak antiferromagnetic couplings with neighboring atoms, e.g., the nitrogen of the NV center. Image Credit: https://www.nature.com/articles/s42005-024-01668-9
Background
Point defects are widely utilized to manipulate the electronic and optical characteristics of semiconductors. Recently, the introduction of paramagnetic defects has begun to alter the magnetic properties of these materials, revealing a range of mesoscopic and microscopic magnetic phenomena.
By reducing the concentration of defects, controllable few-spin systems can be established, facilitating the creation of quantum nodes and qubits based on point defects. In wide-bandgap semiconductors, these point defect qubits exhibit robustness and high coherence, even at elevated temperatures.
The optically addressable spin qubits, exemplified by the silicon vacancy in silicon carbide and the NV center in diamond, maintain prolonged coherence times at room temperature. Consequently, point defect quantum devices are increasingly prominent in various quantum technology applications, including quantum internet and quantum sensin.
Importance of Accurate Hyperfine Tensors
In light element semiconductors, the coherence of spin qubits is compromised by interactions with nuclear spins and paramagnetic defects. In high-purity samples, the magnetic environment of a spin qubit is predominantly influenced by the surrounding nuclear spin bath.
The interaction between point defect spins and nuclear spins is mediated through hyperfine coupling, which is determined by the positions of the nuclear spins and the spatial distribution of the defect's spin density. The hyperfine tensor, which parameterizes the hyperfine term in the spin Hamiltonian, is crucial in this interaction. The elements of the hyperfine tensor can be both calculated using first-principles electronic structure methods and measured via various magnetic resonance techniques.
While the accuracy of the calculated hyperfine tensors or parameters is impressive for nuclear spins close to the defect—within 1-5 Å—the precision diminishes significantly for nuclear spins positioned at greater distances. This decrease in accuracy is largely due to periodic boundary conditions and the limitations of finite-size effects.
The Study
In this study, researchers employed a first-principles code, widely recognized in the industry, to demonstrate that the computed hyperfine parameters' absolute relative error can surpass 100% for the NV center in diamond. They initially showcased the numerical inaccuracies in the hyperfine parameters using the industry-standard VASP code.
To address the methodological shortcomings, the team introduced a real-space integration method and employed a substantially large support lattice that accounted for nuclear spins beyond the supercell boundaries. They conducted extensive calculations for the NV center in diamond using different exchange-correlation functionals and benchmarked their results against existing experimental hyperfine datasets.
For these calculations, diamond supercells containing 1728 and 512 atoms with a central NV center were used. The researchers utilized the Heyd-Scuseria-Ernzerhof (HSE06) and Perdew-Burke-Ernzerhof (PBE) exchange-correlation functionals, applied stringent convergence criteria, and performed Γ-point sampling of the Brillouin zone with a 500 eV cutoff energy for the plane-wave basis set.
The energy threshold for the self-consistent field calculations was set at 10-6 eV for the self-consistent field calculations, and the defect structure was optimized until the most significant force fell below 10-3 eV/Å. For the hyperfine tensor calculations in real space, the convergent spin density from the 1728-atom supercell model was utilized. This model was defined on a finely spaced real-space grid of 0.036 Å, processed through VASP.
Significance of the Study
By implementing the proposed method, researchers achieved a significant enhancement in hyperfine values, achieving a nearly 100-fold reduction in the mean absolute relative error (MARE) compared to the industry-standard VASP code. This substantial improvement was characterized by markedly lower relative mean errors across all measured distances.
In particular, the application of the Heyd-Scuseria-Ernzerhof (HSE06) functional with a 0.2 mixing parameter demonstrated optimal performance for the NV center in diamond, yielding a mean absolute percentage error of just 1.7 % for nuclear spins located 6-30 Å from the NV center. This performance markedly surpassed previous theoretical predictions using VASP, indicating a significant advancement in the accuracy of hyperfine calculations.
The study further highlighted that the remaining discrepancies in the results could likely be attributed to inaccuracies in calculating the Fermi contact term. Moreover, researchers provided highly accurate hyperfine tensors for 104 lattice sites and volumetric hyperfine data with a spatial resolution finer than 0.1 Å. This level of precision is critical for the high-accuracy simulation of NV center quantum nodes, which are pivotal in quantum information processing and for accurately positioning nuclear spins through the comparison of experimental and theoretical hyperfine data.
In summary, this study confirmed that high-accuracy, finite-size effect-free hyperfine tensors can be computed effectively using the proposed integration method. These findings suggest that even more precise theoretical hyperfine data could be obtained by further enhancing numerical accuracy in larger supercells and incorporating more precise experimental data.
Journal Reference
Takács, I., Ivády, V. (2024). Accurate hyperfine tensors for solid state quantum applications: Case of the NV center in diamond. Communications Physics, 7(1), 1-6. https://doi.org/10.1038/s42005-024-01668-9, https://www.nature.com/articles/s42005-024-01668-9
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.
Article Revisions
- Jun 13 2024 - Title changed from "New Method Enhances Hyperfine Accuracy for NV Centers" to "New Method Enhances the Accuracy of Quantum Calculations"