Quantum control theory is a theoretical framework that has been developed to dynamically control and manipulate quantum systems.

Image Credit: agsandrew/Shutterstock.com
With the emergence of quantum mechanics in the early 20th century, controlling quantum phenomena to develop useful devices has been an objective of scientists. Quantum control is a combination of both classical and quantum theories.
Classical Control Theory
Classical control theory was applied in technology such as the steam engine as far back as 1788. In this case, the control method is a series of systematic protocols instructing how to operate a device to perform a desired task. Other everyday devices such as thermostats and washing machines are also examples where classical control theory is implemented. These devices follow a set of routines fed to them by a user. On some occasions, a particular device, a thermostat for example, will act on measurement data that is fed back to it, to maintain a desired level of output.
Quantum Control Theory
Classical control theory cannot adequately govern quantum mechanical operations. The measurable quantities in a quantum system are vastly different from a classical system. Quantum systems are microscopic in nature and exhibit many unique behavioral characteristics due to their small size. For example, quantum entanglement and coherence are properties of quantum mechanics that do not occur in classical systems. Quantum theory is required to control quantum systems.
Quantum control theory is still a developing area of research. A lot of focus has been given to deriving efficient quantum control models in recent years due to the rapid advancements in quantum technology.
Quantum control theory is based on proven traditional control methods. It combines classical control theory with the mathematics of quantum mechanics. This is a non-trivial process that continues to evolve with emerging technology.
Control theory, whether classical or quantum, follows two different methods of implementation. They are open-loop control and closed-loop control. Different mathematical techniques and equations are employed in each of these categories.
Open-Loop Control
In open-loop control theory, the series of operational instructions do not rely on any measurement. This can be thought of as a linear, one-directional operation for simplicity. As shown in figure 1, the controller specifies a set of operational protocols that need to be executed for the system to function as desired.
The quantum mechanical version of open-loop control closely obeys the operational principles of its classical counterpart. The similarities in both quantum and classical, open-loop control methods are that they do not need to be updated with a measurement from the system.
Some variations of open-loop strategies for quantum systems are variable control, Lyapunov-based control, and incoherent control.
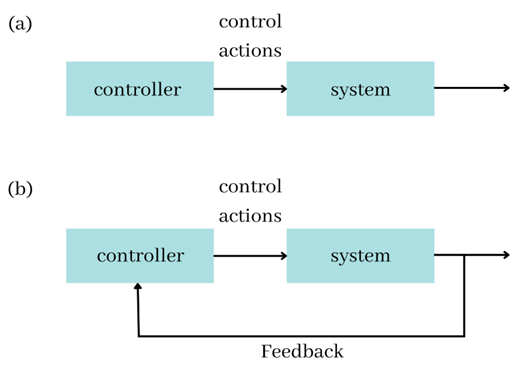
Figure 1: (a) Open-loop control. (b) Closed-loop control
Closed-Loop Control
Closed-loop control requires a measurement of the system being controlled. As shown in figure 1(b), measurements are carried out on the system which are actively fed back to the controller. The controller uses the data acquired from the measurements to adjust different parameters. A closed-loop controller uses the feedback data to augment the system's output.
When closed-loops control techniques are applied to quantum systems, noise is introduced. Many control algorithms have been developed to characterize the noise contributions in quantum control. Closed-loop learning control, quantum filtering, and direct and indirect feedback control are some of the strategies used to mitigate noise in quantum control.
Applications of Quantum Control Theory
Research efforts in physics, applied mathematics, and chemistry benefit greatly from quantum control theory. All quantum technology applications use quantum control theory for control and optimization. Specific quantum technology sectors like quantum sensing, quantum computation, quantum communication, and quantum simulation, depend on control theory to mitigate errors and improve efficiency. This is across all quantum technology platforms, including superconducting circuits, silicon devices, trapped atoms and ions, photonics, and micro-resonators.
In quantum computing, control theory is applied to stabilize the qubit platform against decoherence. Quantum coherence is a vital property that directly affects the performance of a quantum computer. Extending the coherence times of qubits has been a major hurdle in the progress of quantum computing. Consequently, new quantum control models are continuously derived to address the susceptibility of quantum devices against decoherence.
Quantum communication protocols are also optimized using control theory. A future quantum internet relies on quantum memory and quantum repeaters to store, retrieve and relay information. Quantum network nodes are currently developed and tested to transfer entangled quantum data over large distances. Quantum control theory is implemented at each node to optimize resources and efficiency.
In quantum sensing platforms, control theory enables extremely sensitive detection of weak forces. Interactions between the object and the sensor can be isolated and amplified using appropriate control protocols. Here, the instabilities of the quantum hardware and the resulting systematic error contributions are accounted for by the control algorithms.
Quantum simulation platforms consist of many tunable parameters. The extent of controllable variables can be an asset and liability. More parameters allow for a broad range of complex phenomena to be studied. But the number of changeable variables is prone to present more errors. Quantum control theory is an invaluable tool in quantum simulation to monitor all the parameters effectively.
Outlook
Many successful experiments and technological advancements have validated the efficacy of quantum control theory. New quantum control models are continuously being developed and tested. The biggest challenges in scaling quantum devices in the future depend on effective control and optimization of resources. Quantum control theory is rapidly evolving, and more research will enable improved control of quantum systems.
More from AZoM: The Large Hadron Collider Upgrade and the Search for New Physics
References and Further Reading
D. Dong and I. R. Petersen, “Quantum control theory and applications: a survey,” IET Control Theory & Applications, vol. 4, no. 12, pp. 2651– 2671, 2010. https://arxiv.org/abs/0910.2350
H. Mabuchi and N. Khaneja, “Principles and applications of control in quantum systems,” International Journal of Robust and Nonlinear Control, vol. 15, no. 15, pp. 647–667, 2005. https://d-biswa.github.io/Teaching/RM03_Mabuchi_Khaneja_Quantum.pdf
Ignacio R. Sola, Bo Y. Chang, Svetlana A. Malinovskaya, Vladimir S. Malinovsky, Chapter Three - Quantum Control in Multilevel Systems,Editor(s): Ennio Arimondo, Louis F. DiMauro, Susanne F. Yelin,Advances In Atomic, Molecular, and Optical Physics, Academic Press,Volume 67, 2018, Pages 151-256, ISSN 1049-250X, ISBN 9780128142158, https://www.sciencedirect.com/science/article/pii/S1049250X1830003X?via%3Dihub
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.