The time-independent perturbation theory is a fundamental formalism in quantum mechanics that describes a quantum system that is affected by a small time-independent external force. This article can be read in tandem with our piece: What is the Time Dependent Perturbation Theory?

Image Credit: local_doctor/Shutterstock.com
In nature, a dynamical physical system is described as a set of moving particles. The total energy of such a dynamical system is given by the Hamiltonian.
The Hamiltonian
The Hamiltonian is a mathematical definition formulated by Sir William Rowan Hamilton in 1835
The Hamiltonian of a physical system is its total energy given by the sum of the kinetic energy and the potential energy. The Hamiltonian of a classical physical system can be represented as shown in the equation below.
H = K + V
Where H denotes the Hamiltonian, which is the sum of kinetic energy K and potential energy V.
In quantum mechanics, the Hamiltonian of the system is represented by quantum mechanical operators. The kinetic and potential energy expressions are transformed to their associated operator representations as shown below.
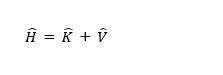
The Schrodinger Equation
The Schrodinger equation, which is a significant landmark in the development of quantum mechanics, is derived when the Hamiltonian is applied to the energy wave function. A wave function is a mathematical description of the quantum state of an isolated quantum system.
In the time-independent Schrodinger equation, the operation produces specific values for the energy called energy eigenvalues. A measurement of an arbitrary dynamic physical system's total energy using the Hamiltonian provides a set of possible solutions.
The harmonic oscillator, the infinite square well, and the hydrogen atom are some examples of problems that can be solved using the Hamiltonian operation and the Schrodinger equation.
Time Independent Perturbation Theory
To understand perturbation theory, it is ideal to analyze a problem that can already be solved using the Schrodinger equation. For example, the hydrogen atom. A perturbation is a small change that is introduced to the system. This change can be an electric or magnetic field or any other subtle force. In the time-independent case, the perturbing force is uniform and does not vary with time.
The small change introduces a perturbation to the total energy of the system or the Hamiltonian of the system. This perturbation distorts the original Hamiltonian. This subtle change can be represented by a new Hamiltonian in the following way;
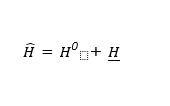
((hereby referred to in the text as H^, Ho, and H_, respectively))
where H^ is the new Hamiltonian, Ho is the original Hamiltonian that can be solved, and H_ is the perturbation that has been introduced.
To solve the new Hamiltonian, the quantum states have to be expanded. The quantum states of the perturbed Hamiltonian can be expanded as superpositions of the known solutions of the unperturbed Hamiltonian. The perturbation can be thought of as the change in solution states from the original states to a new perturbed state. The perturbed states are the original states plus some additional elements that have been introduced by the external force.
The solutions to the original Hamiltonian are used as the basis to describe the solutions to the perturbed Hamiltonian. The energy of the perturbed state is analyzed with a series expansion like the power series or Taylor series. The zeroth term of the series expansion is the unperturbed energy and the other terms represent the first-order correction and the second-order correction and so on. In many cases, considering just the first few terms of the power series give reasonable results. Adding the appropriate correction results in an approximate solution for the perturbed Hamiltonian.
Examples of Time Independent Perturbation Theory
Two examples where time-independent perturbation theory predicts approximate solutions are the Zeeman effect and the Stark effect.
When a homogeneous magnetic field is introduced to a system that has a magnetic dipole moment, like the hydrogen atom, the energy levels are split into sublevels. This effect is called the Zeeman effect. Similarly, the Stark effect is the electric analog to the Zeeman effect. An atom carrying an electric dipole moment, like the hydrogen atom, will get a splitting of its energy levels when an exterior homogeneous electric field is turned on.
While the time-independent perturbation theory is a key fundamental concept widely used in quantum mechanics, it has limitations when computing many-body systems. Many-particle systems present various contributions to the physical nature of the problem that makes the computations impossible to handle. Even in the case of the hydrogen atom, the external field has to be small compared with the electric field inside the atom for the approximation to be accurate.
What is the Time Dependent Perturbation Theory?
References and Further Reading
Griffiths, D., & Schroeter, D. (2018). Introduction to Quantum Mechanics (3rd ed.). Cambridge: Cambridge University Press. doi:10.1017/9781316995433
PAULING, L. AND WILSON, E. B. Introduction to quantum mechanics 2008 - Dover Publications - New York, N.Y.
Reinhold A. Bertlmann. Quantum Group| https://homepage.univie.ac.at |https://homepage.univie.ac.at/reinhold.bertlmann/pdfs/T2_Skript_Ch_8.pdf
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.