As networks develop in size and complexity beyond basic short-distance point-to-point situations, the formation, distribution, and validation of entanglement in multipartite quantum communication networks becomes increasingly important. Multipartite entanglement, in general, allows for applications like increased sensing and multi-user quantum communication protocols. This is explored in research published in the journal Quantum.

Study: Local and scalable detection of genuine multipartite single-photon path entanglement. Image Credit: Yurchanka Siarhei/Shutterstock.com
The difficulty, at its core, is to discover scalable means to actualize these applications while keeping them experimentally viable. On the one hand, the experimental constraints of probabilistic multi-photon sources, particularly in terms of rates, pose significant barriers to the creation of entangled states. On the other hand, the exponential scaling of tomography measurements as the number of parties rises makes state certification impossible even for a small number of parties.
Even for point-to-point communication methods, a change away from photon-pair to announced single-photon entanglement gave considerable scaling gains in the creation and dispersion of entanglement for quantum repeaters.
As shown in Figure 1(a), efficient entanglement distribution between two distant parties via optical fiber can be achieved by providing each party with a source emission signal-idler photon pairs, incorporating the idler modes into a beam splitter at a central station, and placing two detectors at the beam splitter’s output.
As shown in Figure 1 (b), this is a fast technique to get a multipartite entangled state that is close to a W state. Entanglement certification in multipartite quantum communication networks is exceedingly difficult.
To expose genuine multipartite entanglement (GME) without post-selection, researchers built an entanglement witness adapted to the W state. They assumed that the measuring apparatus was well-characterized and that each party i owned a single optical mode with a corresponding bosonic annihilation operator ai.
Experts do not presume that the same state is prepared in each iteration because the photon number statistics are unknown (i.i.d.). The witness is scalable since just two separate measurement settings are required, regardless of the number of parties. Its utility is proven using an experimental setup similar to that shown in Figure 1(c), in which genuine 4- and 8-partite entangled states are detected at high rates and successfully verified.

Figure 1. Heralded multipartite entanglement distribution. (a) Entanglement is distributed between two parties, each having a signal-idler photon pair source (S). The idler modes are combined on a beam splitter and the detection of a single photon after this beam splitter projects the signal modes into a single-photon entangled state. (b) Generalization of the scheme to tripartite states while keeping the local losses low. The aim of this work is to clarify on how entanglement can be detected in this setting. (c) Conceptual schematic of the experiment. Entanglement is distributed among several parties by locally splitting the signal mode into multiple spatial output modes. Image Credit: Caspar, et al., 2022
Methodology
Figure 2 depicts the experimental setup. As a type-II spontaneous parametric down-conversion (SPDC) source, researchers use a heralded single-photon source (HSPS) based on a regularly poled potassium titanyl phosphate (PPKTP) nonlinear crystal.
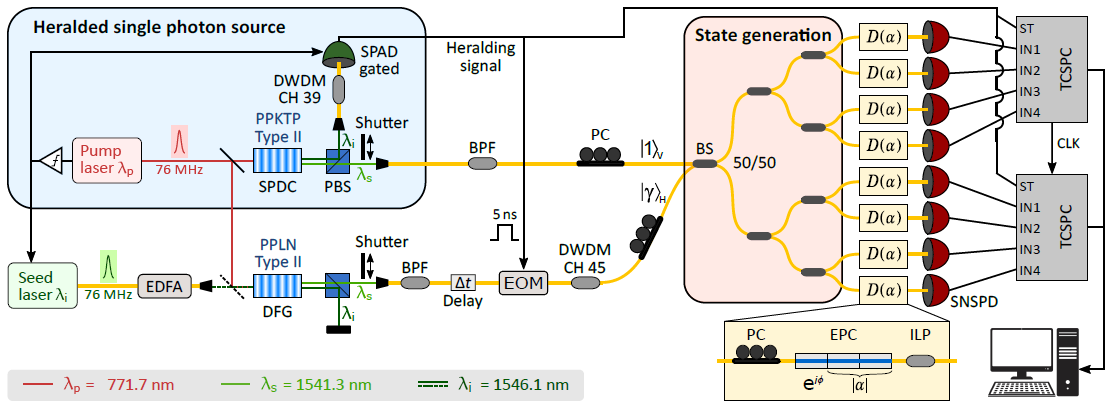
Figure 2. Experimental schematic: A heralded single photon, incident on a cascade of 50/50 fiber beam splitters (BS), is delocalized over spatial modes to generate an 8-partite path-entangled state. Weak coherent states in orthogonal polarization modes are co-propagated with the single-photon state to locally perform displacement-based measurements. See main text for details on the setup and notation. Image Credit: Caspar, et al., 2022
Table 2 shows the experiment’s corresponding values.
Table 2. Evaluation of the witness for N parties with parameters λ and µ according to Eqs. (20) and (32). The mean values o, z and s are associated to the observables 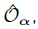 Ƶ and −N2 (N − 1)Πn≥2(1), respectively. The numbers n, m, and l indicate the number of evaluations of o, z and s. Together with the biseparable bound wbisepmax according to Eq. (53), the p-value is calculated using Eq. (69). Note that in order to obtain a p-value of less than 10−10, in the case of N=4 it would suffice to evaluate the observables n = m = l = 4.9 × 105 times, corresponding to a total integration time of less than 130 seconds, and for N=8 it would require n = m = l = 7.8 × 106 evaluations which could be achieved in less than 2100 seconds. Source: Caspar, et al., 2022
Ƶ and −N2 (N − 1)Πn≥2(1), respectively. The numbers n, m, and l indicate the number of evaluations of o, z and s. Together with the biseparable bound wbisepmax according to Eq. (53), the p-value is calculated using Eq. (69). Note that in order to obtain a p-value of less than 10−10, in the case of N=4 it would suffice to evaluate the observables n = m = l = 4.9 × 105 times, corresponding to a total integration time of less than 130 seconds, and for N=8 it would require n = m = l = 7.8 × 106 evaluations which could be achieved in less than 2100 seconds. Source: Caspar, et al., 2022
| N |
λ |
μ |
o |
z |
s |
n |
m |
l |
wbisepmax |
p-value |
| 4 |
2.73 |
102 |
1.1525 |
1.8417 |
-0.0014 |
26747089 |
26755161 |
135905902 |
2.785 |
10−1952 |
| 8 |
8.29 |
151 |
2.5762 |
5.9915 |
-0.0024 |
27611104 |
27576602 |
365370348 |
8.358 |
10−87 |
The spectrum overlap measurement is given in Figure 5. Due to the limited overlap of the fitted Gaussians, HongOu-Mandel visibility is projected to be 99.2%.
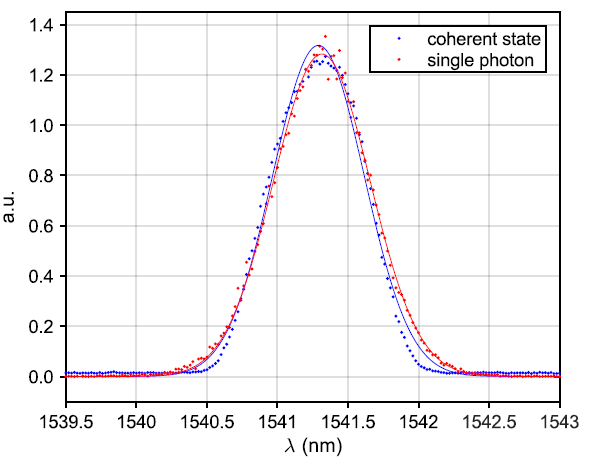
Figure 5. Normalized measured spectra and Gaussian fit of single-photon and coherent states. The spectra are measured with a tunable grating filter with a FWHM of 0.2 nm inserted before the SNSPD. Image Credit: Caspar, et al., 2022
To determine the relative phases between single-photon and coherent states for each spatial mode, polarization is oriented with a polarization controller so that it reaches the first segment of the electronic polarization controller on-axis, as illustrated in Figure 6.
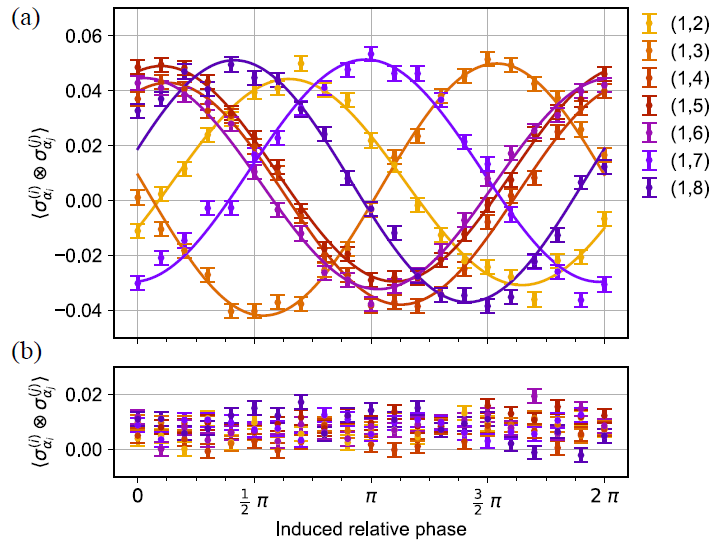
Figure 6. Phase alignment between mode 1 (reference) and all seven other modes. (a) The single-photon state is displaced with α ≈ 0.83 and the first segment of the electronic polarization controller is swept over its full range from 0 to 2π in each non-reference mode. Sinusoidal curves are fitted to the data. (b) Same measurement without the presence of the single-photon state. Image Credit: Caspar, et al., 2022
The displacement amplitudes are calculated using Poissonian count statistics and measuring the coherent state in the absence of the single-photon state, seen in Figure 7.
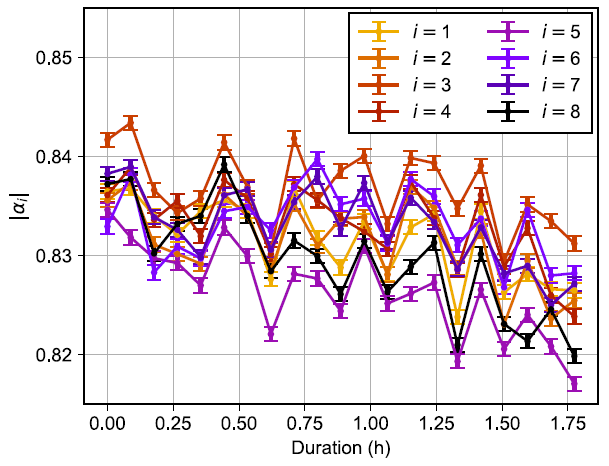
Figure 7. Measurement of the displacement amplitudes |αi| for each spatial output mode i during the data acquisition. For each point, counts are acquired for 1 min. Image Credit: Caspar, et al., 2022
The counts in each mode in the measurement without displacement were normalized to calculate the balance of the produced state, as illustrated in Figure 8.
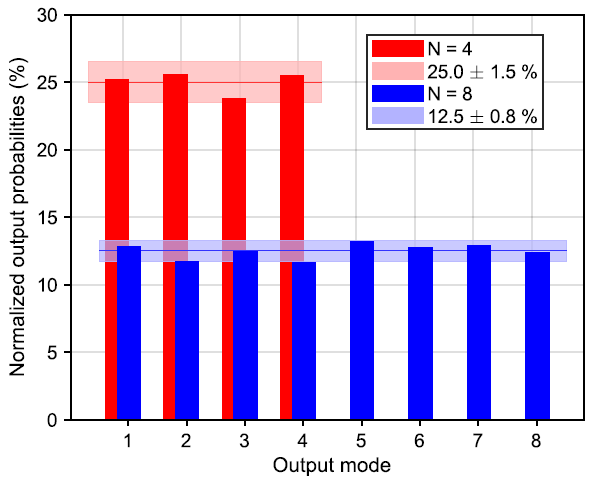
Figure 8. Normalized probabilities of detecting a photon in output mode i ∈ {1, ..., N} in the measurement without displacement. Image Credit: Caspar, et al., 2022
Table 3 shows the probability Pnclick that n detectors will click when measuring the state.
Table 3. Measured probabilities Pnclick that n detectors click in the case of preparing an N-partite state. Further, p1* is an upper bound on the probability of having more than one photon locally in mode 1. Source: Caspar, et al., 2022
| N |
P1click |
P2click |
P3click |
p1* |
| 4 |
0.3106(1) |
3.21(4) · 10−4 |
1.5(8) · 10−7 |
2.89(5) · 10−5 |
| 8 |
0.2678(1) |
2.96(4) · 10−4 |
1.5(8) · 10−7 |
5.4(1) · 10−6 |
The maximum number of parties Nmax, for which the value ⟨Wdc⟩ - wbisepmax -2N2 (N − 1) pdc, is shown in Figure 9 as a function of η for a state, is still positive ρηBS.
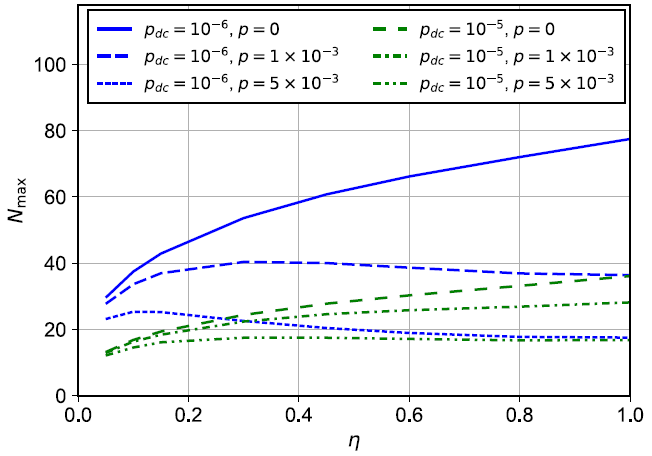
Figure 9. Maximum number of parties Nmax for which the witness is still violated as a function of η for a state ρη. The scaling behavior is shown for input states ρ = (|1⟩⟨1| + p|2⟩⟨2|)/(1 + p) with p ∈ {0, 1 × 10−3, 5 × 10−3} that are measured with detectors suffering from dark counts with probabilities per heralding event of pdc ∈ {10−6, 10−5}. Image Credit: Caspar, et al., 2022
A new detector model with dark counts might enhance the witness, which experts will leave for further research.
Results
The witness is measured for N = 4 and 8 parties in two distinct experimental configurations, and the separable bound is exceeded in both cases, as seen in Table 1. In the case of N = 8, there is higher state loss, owing to another BS’s insertion loss and the four extra SNSPDs’ lower detection efficiency.
Table 1. Measured expectation values wpexp and calculated separable bounds wbisepmax of the N-partite entanglement witness for states with vacuum contributions p0 and upper bounds p∗ on the probability of having more than one photon, see Ineq. (2). The p-value for the null-hypothesis that the state ρ is biseparable is calculated according to Appendix D. Source: Caspar, et al., 2022
| N |
p0 |
p* |
wpexp |
wbisepmax |
p-value |
| 4 |
0.6891(1) |
4.36(5) · 10−4 |
2.993(2) |
2.785 |
10−1952 |
| 8 |
0.7319(1) |
3.40(4) · 10−4 |
8.565(4) |
8.358 |
10−87 |
For N = 8, researchers examined the data further by computing the expected value and separable bound of the n-partite witness for each of the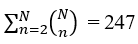 possible subsets of n Є {2,..., N} out of N parties.
possible subsets of n Є {2,..., N} out of N parties.
The findings are shown in Figure 3. This witness is predicted to identify GME for all subsets of parties in a given state; nevertheless, these findings imply that the witness is also suited to detect GME with a significant probability of having a vacuum for all parties p0. The reason that the witness violation wpexp - wbisepmax differs for different selections of the same number of parties n is due to differences in transmission and detection efficiency.
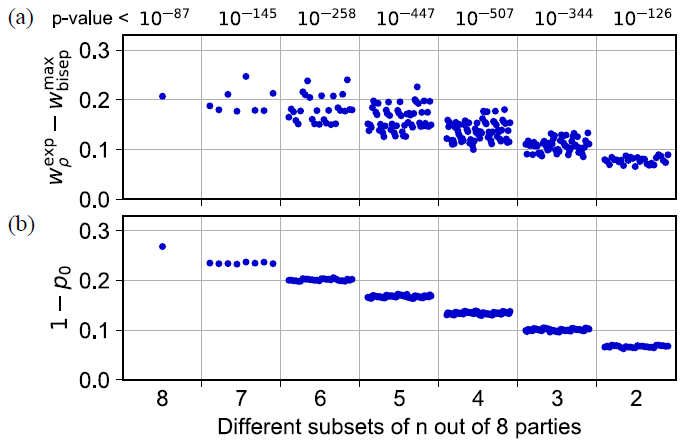
Figure 3. Results of the witness for N = 8. The witness is applied to all possible different subsets of n out of N parties where the discarded parties are traced out. The plots show (a) the violation of the witness wpexp - wbisepmax with the maximum p-value for each fixed number of subsets indicated on top and (b) 1−p0 where p0 is the probability of the vacuum component for each subset of parties. Image Credit: Caspar, et al., 2022
Discussion
The witness’s scalability with the number of parties N is discussed. To begin, experts wanted to underline that the witness solely rests on three measurements. Two of them, p0 and p*, may be measured using a single setting per party that corresponds to no displacement.
The final quantity is evaluated using displacement operations in a second setting. This differs from other approaches in which the total number of settings rises polynomially with N and strategies based on state tomography in which it grows exponentially with N.
For each bipartition of the N parties in two groups, researchers just need to compute the maximum eigenvalue of an N x N matrix. The computational difficulty of building the matrix and determining its highest eigenvalue scales significantly better for every bipartition than the prior reported approaches based on a relaxation of a semi-definite optimization over the biseparable states of N qubits.
As demonstrated in Figure 4, lowering the chance of obtaining a two-photon state increases the amount of parties that the witness may detect GME.
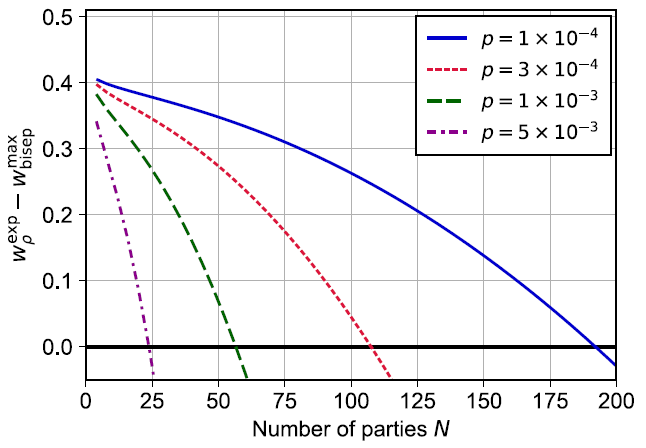
Figure 4. Calculation of the witness violation wpexp - wbisepmax as a function of the number of parties N for a state ρ = (|1⟩⟨1| + p|2⟩⟨2|)/(1 + p) input to an N-port beam splitter after undergoing a loss channel with transmission η = 0.3. The two-photon probability p = 5 × 10−3 is a good approximation for the state generated in the experiment. In this calculation, we assume a perfectly balanced state and fix the displacement amplitude for the measurement to α = √ln 2 ≈ 0.83 f. Image Credit: Caspar, et al., 2022
This would allow for the illustration of GME for up to 23 parties in a condition comparable to that used in the experiment. Researchers verify that this has no effect on GME demonstration in this experiment, and also study scalability in the presence of dark counts.
Conclusion
In future quantum networks, the established witness is ideally suited for efficient verification of multipartite single-photon route entanglement. In a technique where each party maintains a photon-pair source and one photon of each pair is delivered to a central multi-port beam splitter that eliminates the which-path information, highly entangled multipartite states might be communicated at high speeds.
Local losses may be maintained low in this manner because the increased distance between parties just lowers the heralding rate. Such a method, when combined with quantum memory, has the potential to be used in applications that rely on dispersed W states. The necessity for phase stability in long fiber lines remains an experimental problem in such a setup.
More from AZoM: How Quantum Mechanics Won the 2022 Nobel Prize in Physics
Journal Reference:
Caspar, P., Oudot, E., Sekatski, P., Maring, N., Martin, A., Sangouard, N., Zbinden, H. and Thew, R. (2022) Local and scalable detection of genuine multipartite single-photon path entanglement. Quantum, 6, p.671. Available Online: https://quantum-journal.org/papers/q-2022-03-22-671/.
References and Further Reading
- Kimble, H. J (2008) The quantum internet. Nature, 453, pp. 1023–1030
- Wehner, S., et al. (2018) Quantum internet: A vision for the road ahead. Science, 362, p. eaam9288 (2018). https://doi.org/10.1126/science.aam9288.
- Kómár, P., et al. (2014) A quantum network of clocks. Nature Physics, 10, pp. 582–587 doi.org/10.1038/nphys3000.
- Liu, L-Z., et al. (2021) Distributed quantum phase estimation with entangled photons. Nature Photonics, 15, pp. 137–142. doi.org/10.1038/s41566-020-00718-2.
- Murta, G., et al. (2020) Quantum Conference Key Agreement: A Review Advanced Quantum Technologies, 3, p. 2000025. doi.org/10.1002/qute.202000025.
- Lipinska, V., et al. (2018) Anonymous transmission in a noisy quantum network using the W state. Physical Review A, 98, 052320. doi.org/10.1103/PhysRevA.98.052320.
- Zhong, H-S., et al. (2018) 12-photon entanglement and scalable scattershot boson sampling with optimal entangled-photon pairs from parametric down-conversion. Physical Review Letters, 121, p. 250505. doi.org/10.1103/PhysRevLett.121.250505.
- Daniel F. V., et al. (2001) Measurement of qubits. Physical Review A, 64, 052312. doi.org/10.1103/PhysRevA.64.052312.
- Sangouard, N., et al. (2011) Quantum repeaters based on atomic ensembles and linear optics. Reviews of Modern Physics, 83, 33–80. doi.org/10.1103/RevModPhys.83.33.
- Duan, L-M., et al. (2001) Long-distance quantum communication with atomic ensembles and linear optics. Nature, 414, pp. 413–418. https://doi.org/10.1038/35106500.
- Simon, C., et al. (2007) Quantum Repeaters with Photon Pair Sources and Multimode Memories. Physical Review Letters, 98, 190503. doi.org/10.1103/PhysRevLett.98.190503.
- Minář, J., et al. (2008) Phase-noise measurements in long-fiber interferometers for quantum-repeater applications. Physics Review Letters A, 77, P. 052325. doi.org/10.1103/PhysRevA.77.052325.
- Chou, C-W., et al. (2005) Measurement-induced entanglement for excitation stored in remote atomic ensembles. Nature, 438, 828–832. doi.org/10.1038/nature04353.
- Slodička, L., et al. (2013) Atom-Atom Entanglement by Single-Photon Detection Physical Review Letters, 110, p. 083603. doi.org/10.1103/PhysRevLett.110.083603.
- Delteil, A., et al. (2016) Generation of heralded entanglement between distant hole spins. Nature Physics, 12, pp. 218–223. doi.org/10.1038/nphys3605.
- Stockill, R., et al. (2017) Phase-Tuned Entangled State Generation between Distant Spin Qubits. Physical Review Letters, 119, p. 010503. doi.org/10.1103/PhysRevLett.119.010503.
- Humphreys, P. C., et al. (2018) Deterministic delivery of remote entanglement on a quantum network. Nature, 558, pp. 268–273. doi.org/10.1038/s41586-018-0200-5.
- Lago-Rivera, D., et al. (2021) Telecom-heralded entanglement between multimode solid-state quantum memories. Nature, 594, pp. 37–40. doi.org/10.1038/s41586-021-03481-8.
- Caspar, P., et al. (2020) Heralded Distribution of Single-Photon Path Entanglement. Physical Review Letters, 125, p. 110506. doi.org/10.1103/PhysRevLett.125.110506.
- Yu, Y., et al. (2020) Entanglement of two quantum memories via fibers over dozens of kilometers. Nature, 578, pp. 240–245. https://doi.org/10.1038/s41586-020-1976-7.
- Dür, W., et al. (2000) Three qubits can be entangled in two inequivalent ways. Physical Review A, 62, p. 062314. doi.org/10.1103/PhysRevA.62.062314.
- Gottesman, D., et al. (2012) Longer-Baseline Telescopes Using Quantum Repeaters. Physical Review Letters, 109, p. 070503. doi.org/10.1103/PhysRevLett.109.070503.
- Khabiboulline, E. T., et al. (2019) Optical Interferometry with Quantum Networks. Physical Review Letters, 123, p. 070504. doi.org/10.1103/PhysRevLett.123.070504.
- Khabiboulline, E. T., et al. (2019) Quantum-assisted telescope arrays. Physical Review A, 100, p. 022316. doi.org/10.1103/PhysRevA.100.022316.
- Morin, O., et al. (2013) Witnessing Trustworthy Single-Photon Entanglement with Local Homodyne Measurements. Physical Review Letters, 110, p. 130401. doi.org/10.1103/PhysRevLett.110.130401.
- Monteiro, F., et al. (2015) Revealing Genuine Optical-Path Entanglement. Physical Review Letters, 114, p. 170504. doi.org/10.1103/PhysRevLett.114.170504.
- Papp, S. B., et al. (2009) Characterization of Multipartite Entanglement for One Photon Shared Among Four Optical Modes. Science, 324, pp. 764–768. doi.org/10.1126/science.1172260.
- Gräfe, M., et al. (2014) On-chip generation of high-order single-photon W-states. Nature Photonics, 8, 7pp. 91–795. doi.org/10.1038/nphoton.2014.204.
- Paris, M. G. A., et al. (1996) Displacement operator by beam splitter. Physics Letters A, 217, pp. 78–80. doi.org/10.1016/0375-9601(96)00339-8.
- Vivoli, V. C., et al. (2015) Comparing different approaches for generating random numbers device-independently using a photon pair source. New Journal of Physics, 17, p. 023023. doi.org/10.1088/1367-2630/17/2/023023.
- Hoeffding, W., et al. (1963) Probability Inequalities for Sums of Bounded Random Variables. Journal of the American Statistical Association, 58, pp. 13–30. doi.org/10.1080/01621459.1963.10500830.
- Bruno, N., et al. (2014) Generation of tunable wavelength coherent states and heralded single photons for quantum optics applications. Optics Communications, 327, pp. 17–21. doi.org/10.1016/j.optcom.2014.02.025.
- Caloz, M., et al. (2018) High-detection efficiency and low-timing jitter with amorphous superconducting nanowire single-photon detectors. Applied Physics Letters, 112. doi.org/10.1063/1.5010102.
- Mosley, P J (2007) Generation of Heralded Single Photons in Pure Quantum States'' thesis.