Proof of Phase Transition Puts an End to a Long-Standing Debate

By Skyla BailyMay 23 2022

Quantum theorists generally speak of “phase transitions” regarding a specific situation where a certain system’s parameter varies slightly and, as a result, the ground state experiences a crossover. The properties of exactly solvable many-fermion models of the Lipkin kind, which perform a role in nuclear physics similar to the Hubbard model in solid-state physics, were investigated using recent information techniques in a study published in the journal Quantum Reports.

Study: Statistical Quantifiers Resolve a Nuclear Theory Controversy. Image Credit: Ekaterina Kulaeva/Shutterstock.com

New statistical tools derived from information theory—information measures and complexity measures—have greatly improved the understanding of finite, quantum many-body systems. They were used to discuss various aspects of molecules, atoms, and atomic nuclei. Nuclear systems rarely allow for precise analytical treatment. As a result, the majority of concurrent theoretical research relies on numerical solutions.

The study revisits the Lipkin sort of exactly solvable (finite) fermion model. The canonical ensemble methodology accurately describes the associated structural details. The research also analyzes the details of the ground state phenomenology at low enough temperatures T.

Methodology

Gibbs’ canonical ensemble methodology was used to investigate the concomitant (statistical) order–disorder transactions in this study. A uniform distribution is usually associated with the maximum statistical disorder because all micro-states are equally probable.

The disequilibrium D is a statistical quantifier that expands as the degree of order increases.

Lipkin-like models are the most basic nontrivial finite many-fermion systems that can be solved precisely. The researchers focused on the Abecasis–Faessler–Plastino (AFP) model, which is linked to Lipkin.

It is a simplified nuclear model that represents two-level nuclei. A complex discrete spectrum, as well as a continuous spectrum, can be seen in nuclear spectra. Only the two lowest-lying levels are retained in the AFP model, which yields their exact energies and eigenvectors.

The AFP model deals with N = 2Ω fermions scattered among (2 Ω)-fold degenerate single-particle (sp) levels. An sp energy gap separates the two AFP energy levels. There are four sp microstates, but only two-level energies that degenerate.

The AFP Hamiltonian was devised by AFP. The researchers called v the coupling constant; it is the control parameter of the system and performs a vital role in the statistical considerations.

The most important feature of the AFP model is that it shows a level-crossing in ground-state energy. The ground state level (gsl) is, of course, the lowest of the Hamiltonian’s eigenvalues. The level transitions are referred to as phase transitions informally.

After numerically diagonalizing the matrices, the energy-eigenvalues for both Hamiltonians were noted. With these statistical mechanics, calculations can be carried out in the canonical ensemble.

The main thermal quantifiers were derived from the partition function Z, which is constructed from the probabilities associated with concomitant microscopic states with energies Ei. Other quantifiers were developed 25 years ago. They are dependent on the coupling constant of the concomitant two-body interaction.

The researchers also used a new thermal quantifier called the thermal efficiency η.

Results and Discussion

The AFP model is confirmed to have a phase transition (PT) at a critical value for v that is dependent on N. This was countered by the discovery that if v is replaced with v/N, the PT vanishes. The study tries to resolve this debate using the thermal efficiency metric (v).

It shows the behavior of some of the information-theoretic quantifiers (vertical axis) versus the interaction strength v (horizontal axis). Figure 1 shows AFP (red) and its Lipkin counterpart, L, for comparison (blue).

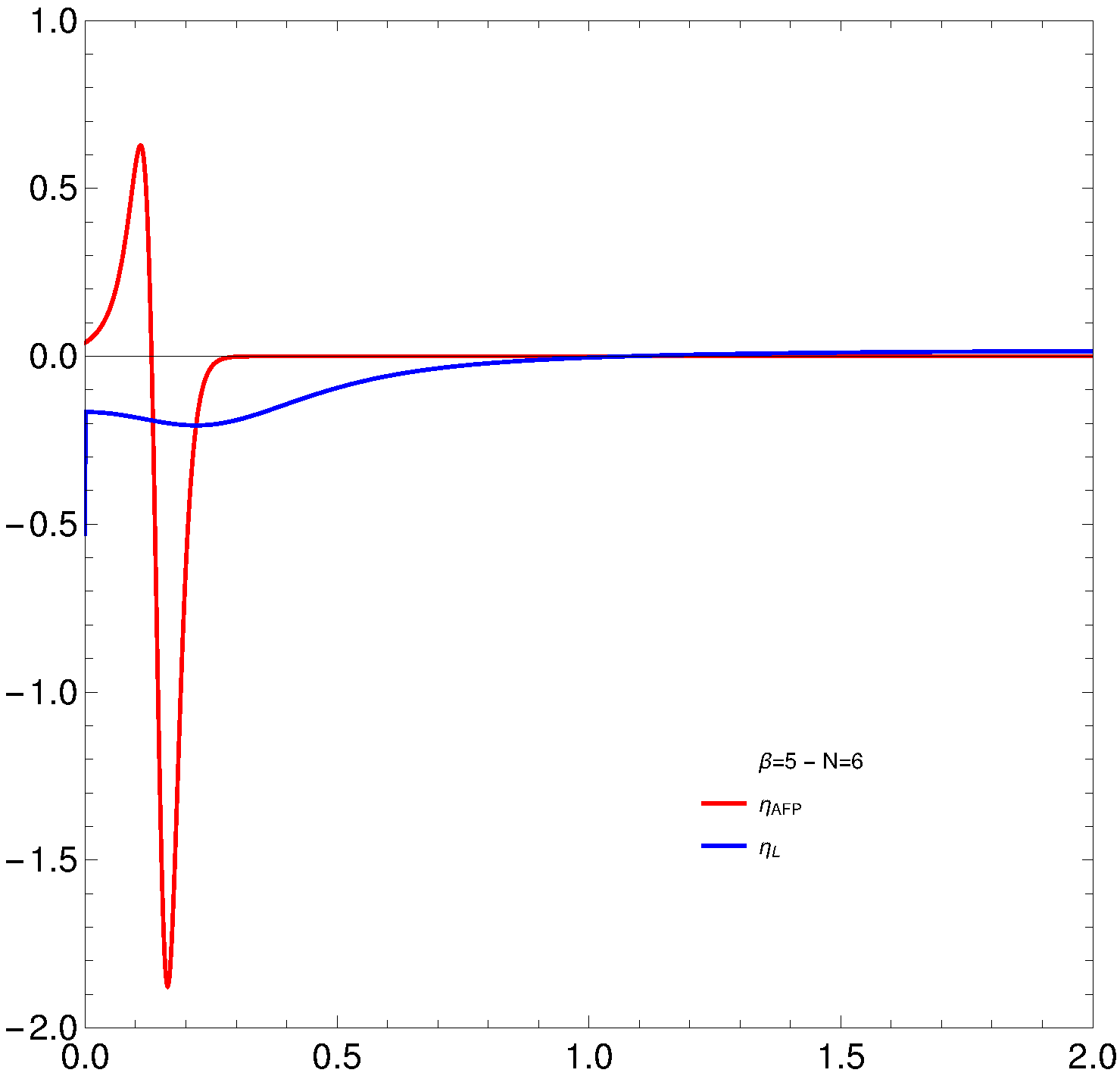
Figure 1. η_AFP (red) and Lipkin’s η_L (blue) vs. v, for N = 6 and the low temperature β = 5. Note that η_AFP (red) clearly detects a phase transition. There is none for the Lipkin model. Image Credit: Monteoliva, et al., 2022

Figure 2 is identical to Figure 1, with the exception that it shows the state of disequilibrium. The ground state becomes disordered between two different micro-states.

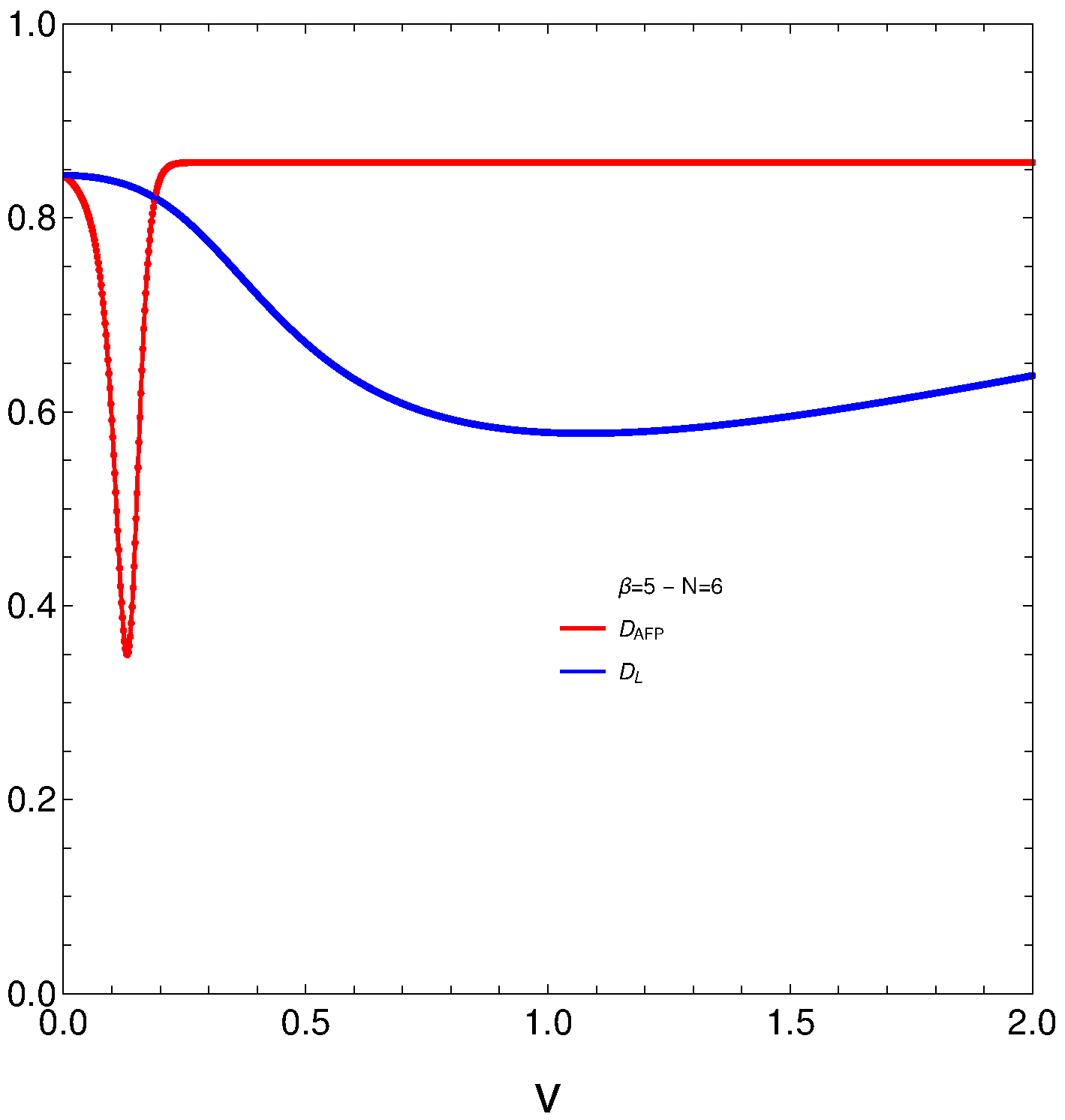
Figure 2. Vertical axis: D_AFP (red) and Lipkin’s D_L (blue) versus v (horizontal axis). The remaining details are as in Figure 1. Image Credit: Monteoliva, et al., 2022

Figure 3 shows the phase transition’s N-dependence. The critical v values decrease as N increases.

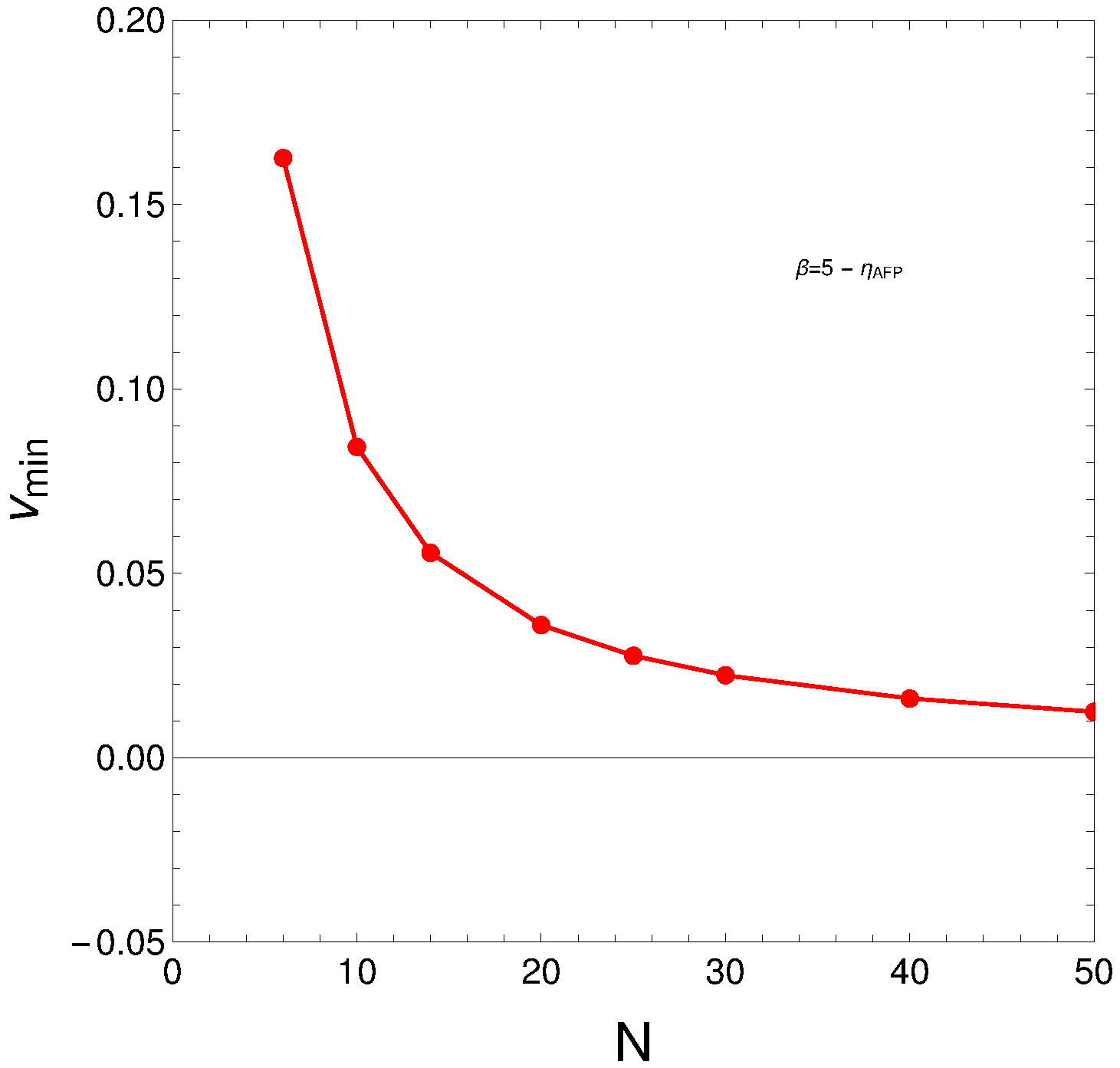
Figure 3. Critical v values versus N. Note that N > 250 does not make sense in a nuclear context. Image Credit: Monteoliva, et al., 2022

The above-mentioned phase transitions were argued to be a ruse to avoid replacing v with v/N. However, this is not the case. The same is depicted in Figures 4 and 5 for the AFP model.

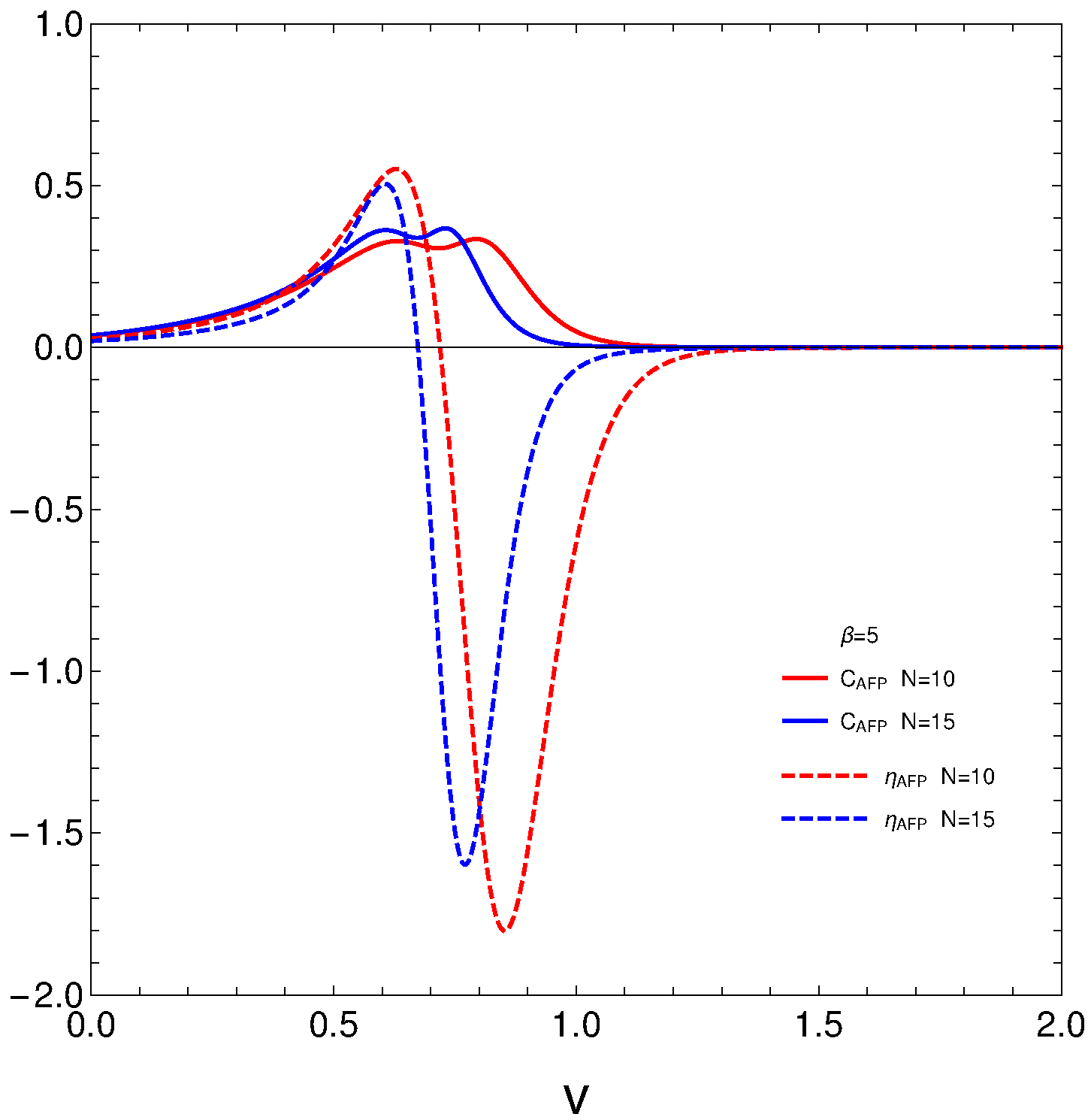
Figure 4. Complexity C (continuous line) and ηAFP (dashed) plotted versus v. The effective coupling constant is v/N. Two N values are used. Image Credit: Monteoliva, et al., 2022

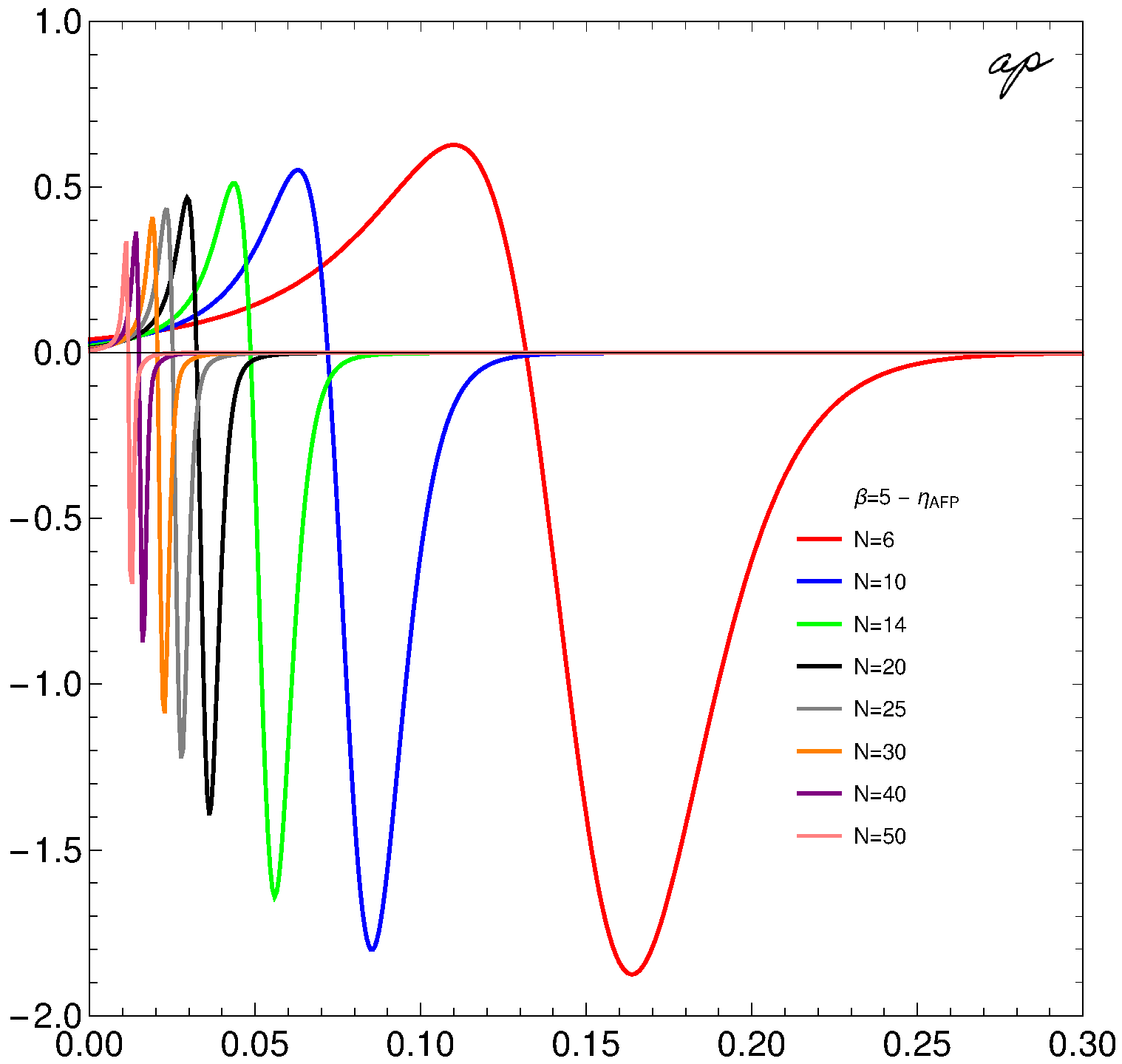
Figure 5. ηAFP plotted versus v. The effective coupling constant is v/N. Eight different N values are used. A different color is assigned to each value, as indicated in the graph. Image Credit: Monteoliva, et al., 2022

Conclusion

The quantum statistics of a well-known finite many-nucleon system that is exactly solvable were discussed. The researchers investigated at a low enough temperature to ensure that the statistical picture accurately reflected the characteristics of the lowest-keying energy levels. Thermal efficiency and statistical complexity were the main protagonists.

The AFP model exhibited ground-state crossovers (phase transitions) regardless of whether N-renormalized coupling constants are used or not. The fact that C has two peaks is irrefutable proof of phase transitions, putting an end to a long-standing debate.

Journal Reference:

Monteoliva, D., Plastino, A., Plastino, A. R. (2022) Statistical Quantifiers Resolve a Nuclear Theory Controversy. Quantum Reports, 4(1), pp. 127–134. Available at: https://www.mdpi.com/2624-960X/4/1/9/htm

References and Further Reading

1. Hubbard, J (1963) Electron Correlations in Narrow Energy Bands. Proceedings of the Royal Society of London, 276, pp. 238–257. doi.org/10.1098/rspa.1963.0204.
2. Liu, Y (2011) Exact solutions to nonlinear Schrodinger equation with variable coefficients. Applied Mathematics and Computation, 217, p. 5866. doi.org/10.1016/j.amc.2010.12.072.
3. Frank, R (2013) Quantum criticality and population trapping of fermions by non-equilibrium lattice modulations. New Journal of Physics, 15, p. 123030.
4. Lubatsch, A & Frank R (2019) Evolution of Floquet topological quantum states in driven semiconductors. European Physical Journal B, 92, p. 215. doi.org/10.1140/epjb/e2019-100087-0.
5. Otero, D., et al. (1981) Surprisal Approach to Cold Fission Processes. Physics Letters, 98, p. 225. doi.org/10.1016/0370-2693(81)90001-0.
6. Satuła, W., et al. (1998) Odd-Even Staggering of Nuclear Masses: Pairing or Shape Effect? Physical Review Letters, 81, p. 3599. doi.org/10.1103/PhysRevLett.81.3599.
7. Dugett, T., et al. (2001) Pairing correlations. II. Microscopic analysis of odd-even mass staggering in nuclei. Physical Review C, 65, 014311. doi.org/10.1103/PhysRevC.65.014311.
8. Ring P & Schuck P (1980) The Nuclear Many-Body Problem; Springer: Berlin/Heidelberg, Germany.
9. Uys, H., et al. (2001) Generalized statistics and high-Tc superconductivity. Physics LettersA, 289, p. 264. doi.org/10.1016/S0375-9601(01)00587-4.
10. Kruse, M.K.G., et al. (2005) Landau-Ginzburg method applied to finite fermion systems: Pairing in nuclei. European Journal of Physics A, 25, p. 339.
11. de Llano M & Tolmachev V V (2003) Multiple phases in a new statistical boson fermion model of superconductivity. Physica A, 317, p. 546. doi.org/10.1016/S0378-4371(02)01348-1.
12. Xu, F.R., et al. (1999) Mean-field and blocking effects on odd-even mass differences and rotational motion of nuclei. Physical Review C, 60, p. 051301. doi.org/10.1103/PhysRevC.60.051301.
13. Häkkinen, H., et al. (1997) Universal Shapes of Small Fermion Clusters. Physical Review Letters, 78, p. 1034. doi.org/10.1103/PhysRevLett.78.1034.
14. Lipkin, H.J., et al. (1965) Validity of many-body approximation methods for a solvable model: (I). Exact solutions and perturbation theory. Nuclear Physics, 62, pp. 188–198. doi.org/10.1016/0029-5582(65)90862-X.
15. Co, G & De Leo, S (2018) Analytical and numerical analysis of the complete Lipkin–Meshkov–Glick Hamiltonian. International Journal of Modern Physics, 27, p. 1850039. doi.org/10.1142/S0218301318500398.
16. Reif, F (1965) Fundamentals of Statistical and Thermal Physics; McGraw Hill: New York, NY, USA.
17. Ruiz, R. L., et al. (1995) A statistical measure of complexity. Physics Letters A, 209, p. 321. doi.org/10.1016/0375-9601(95)00867-5.
18. Arrachea, L., et al. (1992) Maximum Entropy Approach to Critical Phenomena in Finite Quantum Systems. Physical ReviewA, 45, p. 44. doi.org/10.1103/PhysRevA.45.7104.
19. Abecasis, S. M., et al. (1969) Application of the Multi Configuration Hartree-Fock Theory to a Simple. Particles of the Standard Model of particle physics, 218, p. 394. doi.org/10.1007/BF01670019.
20. Feng, D H & Gilmore, R G (1982) Critical properties of a generalized pseudospin Hamiltonian. Physical ReviewC, 26, p. 1244. doi.org/10.1103/PhysRevC.26.1244.
21. Bozzolo, G., et al. (1981) Maximum Overlap, Atomic Coherent States and the Generator Coordinate Method. Nuclear Physics A, 356, p. 48. doi.org/10.1016/0375-9474(81)90117-2.
22. López-Ruiz, R (2013) A information-theoretic Measure of Complexity. In Concepts and Recent Advances in Generalized Information Measures and Statistics, Bentham Science Books: New York, NY, USA, pp. 147–168.
23. Martin, M.T., et al. (2006) Generalized information-theoretic complexity measures: Geometrical and analytical properties. Physica A, 369, p. 439. doi.org/10.1016/j.physa.2005.11.053.
24. Dehesa, J.S., et al. (2009) Configuration complexities of hydrogenic atoms. European Physical Journal D, 55, p. 539. doi.org/10.1140/epjd/e2009-00251-1.
25. Esquivel, R.O., et al. (2011) Information-theoretical complexity for the hydrogenic abstraction reaction. Molecular Physics, 109, p. 2353. doi.org/10.1080/00268976.2011.607780.
26. Pennini F & Plastino A (2017) Disequilibrium, thermodynamic relations, and Renyi’s entropy. Physics Letters A, 381, p. 212. doi.org/10.1016/j.physleta.2016.11.023.
27. Martin, M.T., et al. (2003) Information-theoretic complexity and disequilibrium. Physics LettersA, 311, p. 126. doi.org/10.1016/S0375-9601(03)00491-2.
28. Pennini, F., et al. (2021) Thermal–Statistical Odd–Even Fermions’ Staggering Effect and the Order–Disorder Disjunction. Entropy, 23, p. 1428. doi.org/10.3390/e23111428.
29. Nigmatullin, R & Prokopenko, M. (2021) Thermodynamic efficiency of interactions in self-organizing systems. Entropy, 23, p. 757. doi.org/10.3390/e23060757.
30. Pennini, F & Plastino A (2018) Complexity and disequilibrium as telltales of superconductivity. Physica A, 506, pp. 828–834. doi.org/10.1016/j.physa.2018.05.003.