Jan 22 2016
Rice University theoretical physicist Matthew Foster has won a coveted National Science Foundation (NSF) CAREER Award, which includes a five-year grant to support his research on quantum materials.
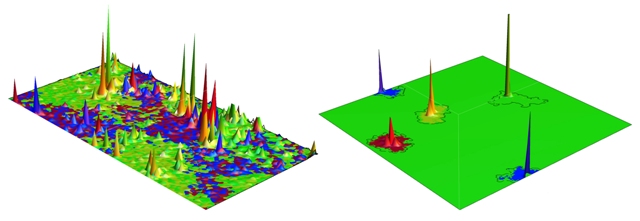Shown in this image are one-electron wave functions that can occur in a disordered two-dimensional material. The left image depicts four different "multifractal" wave functions (red, blue, green and orange). An electron occupying one of these can conduct electricity. The right image depicts four Anderson localized wave functions. An electron occupying one of these is trapped close to the position of the peak and cannot conduct. (Image by Yang-Zhi Chou and Matthew Foster/Rice University)
CAREER Awards are among the NSF’s most competitive, and fewer than 400 are given in a typical year. According to the NSF, they are given in “support of junior faculty who exemplify the role of teacher-scholars through outstanding research, excellent education and the integration of education and research within the context of the mission of their organizations.”
Foster, an assistant professor of physics and astronomy, joined Rice in 2012. His primary research interest is in condensed matter dynamics, particularly the complex behavior of “many-body systems,” like the billions of trillions of electrons that are found in even the tiniest sample of a typical metal or unconventional superconductor.
Quantum materials are a broad class that includes unconventional superconductors and other compounds in which quantum physics plays an essential role in bringing about strange electronic and magnetic behaviors. If better understood, quantum materials could be used in quantum computers, superefficient power grids and other futuristic technologies.
“The complexity of these systems creates challenges,” Foster said. While the equations governing quantum mechanics were laid down about 100 years ago, even the largest and fastest supercomputers cannot solve the equations for models containing more than a few dozen atoms.
“You can’t just put an interesting quantum problem in a computer and solve it,” Foster said. “As you add to the number of particles, the problem becomes exponentially harder to solve.”
Foster, whose undergraduate training was in engineering, said he often brings a more mathematical approach to theory than his colleagues. He was awarded more than $480,000 to support his CAREER research, in which he plans to apply statistical methods originally developed for “Anderson localization” physics to describe the behavior of quantum many-body systems in new ways.
Anderson localization refers to a well-understood phenomenon that explains how a single electron can become “localized,” or locked in place, in the presence of disorder. Disorder means impurities, vacancies or other imperfections in a sample of a given material; some amount of disorder is always present in real materials. Localization occurs because electrons behave like waves according to quantum mechanics, and the locking in place is a wave interference phenomenon. To imagine how this happens, Foster suggests envisioning an electron moving down a wire that’s just one atom thick. The electron can move only in one dimension, so it’s subject to any perturbations that might block its movement in that dimension. The localization of individual electrons has played a crucial role in many key discoveries in quantum materials physics in the past 50 years, including the quantum Hall effect, which led to two Nobel prizes.
Thanks to theoretical insights within the past decade, Foster said, physicists now believe that many-body localization (MBL) — a case similar to Anderson localization wherein a macroscopic system of many electrons becomes locked — can occur at non-zero, even high temperatures. Foster said this was initially very surprising, because making quantum materials “hot” tends to make them “more classical, less subject to quantum weirdness.”
Studying how this might occur is far more complex than the single-body case, particularly if the electrons are free to move in two or three dimensions, he said. Nevertheless, it may be possible to use mathematical tools developed for Anderson localization to learn something useful about these MBL states.
“What I’ve proposed are some very specific attacks on the problem, where I think I have an inroad that other people don’t because of some of the training that I’ve had,” Foster said. “I have certain technical tools, certain analytical methods that I have used in the past to study zero temperature Anderson localization transitions that could be useful in making progress.”
In developing theory, physicists often try to work out the details for a perfect system without any imperfections or disorder. This ideal state, which is referred to as translationally invariant, is useful because it frees one to think only about the fundamental physics at work in a given situation, but it can also make it difficult to apply the model in the real world, Foster said.
“All quantum materials consist of many, many electrons — 10 to the 23 electrons — interacting with each other, usually in a random environment, because there are always impurities in your samples,” he said. “What’s interesting about MBL is that it forces you to think differently about many-body systems. Rather than trying to figure out exactly what ground state the system chooses, MBL offers us a way to say, ‘What if I look at the different types of states that would be possible? If I can treat those statistically, maybe I can say something about what’s actually being measured in an experiment.’”
An educational component of the project aims to make modern mathematical tools more accessible to undergraduate physics majors by emphasizing algorithms and visualization. Foster said physics researchers often make use of innovative mathematical techniques developed in the 20th century. Despite this, most physics undergraduate and graduate students are trained using mathematics that was developed more than 100 years ago. To bring modern mathematical tools into the classroom, Foster plans to create learning modules that use an algorithmic, problem-solving approach and make them freely available online.
“Some of this is material that I only learned after I got my Ph.D.,” he said. “In some cases, applying these techniques isn’t that complicated, but it does require a good bit of practice. The modules that I hope to write would make it easier for physics students to train themselves in these methods, and the materials might also find use in innovative classes that aim to bring more modern mathematics into the physics curriculum.”
Source: http://www.rice.edu/