In a paper recently published in the journal Entropy, the authors reviewed Monte Carlo-based techniques, specifically the path integral (PI) Monte Carlo technique, for studying quantum magnets with long-range interactions.
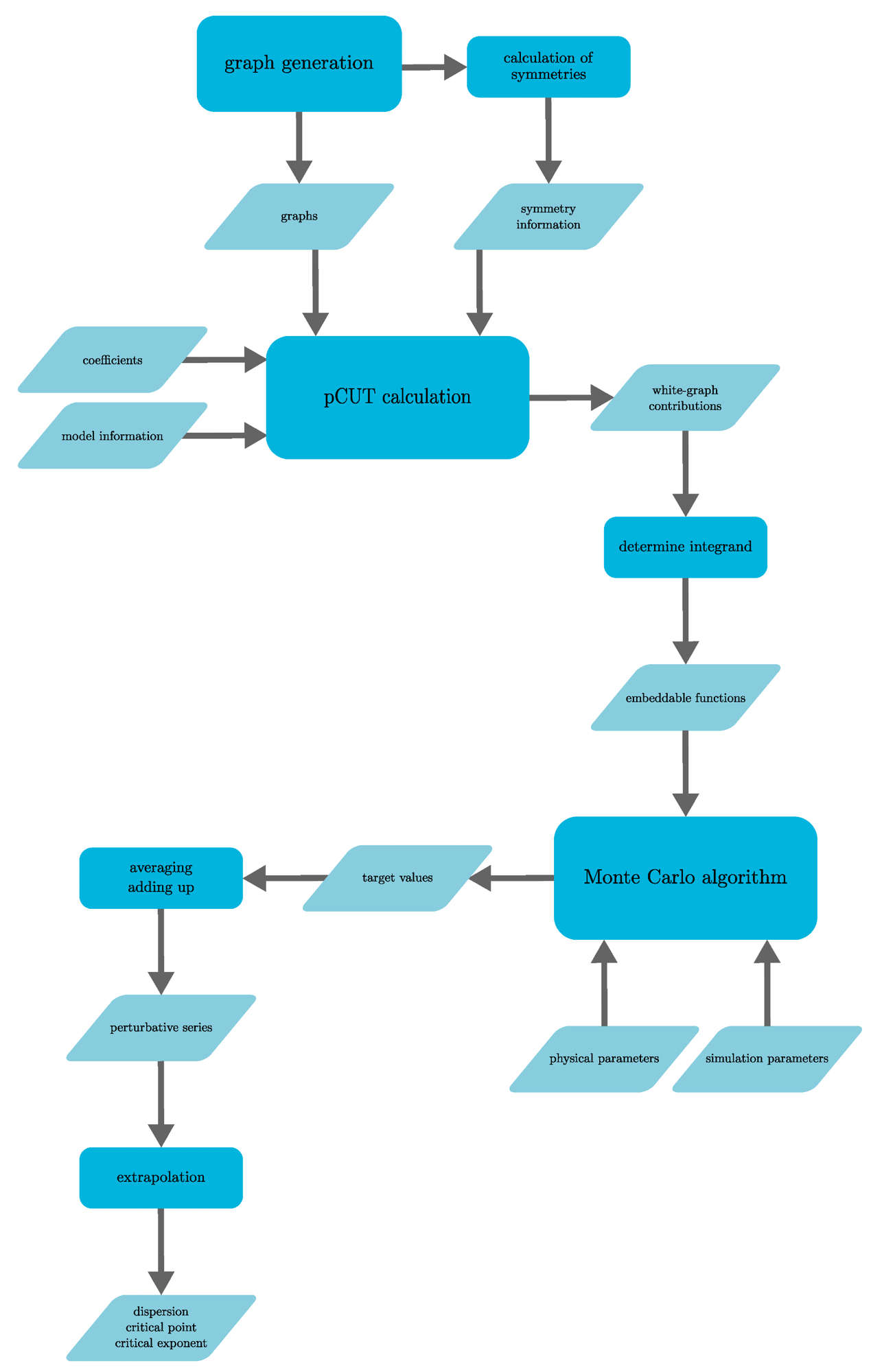The workflow of the presented pCUT+MC method consists of several steps. There are three major steps. First, there is the graph generation, which only has to be performed once. Second is the calculation of the graph contributions with the pCUT method, and third is the Monte Carlo algorithm to embed the contributions on the lattice to determine the perturbative series of the quantity of interest in the thermodynamic limit. Image Credit: https://www.mdpi.com/1099-4300/26/5/401
Background
In condensed matter physics and quantum optics, long-range interactions are important for different quantum systems. Specifically, by controlling quantum-optical platforms, deep insights can be gained into long-range interaction-induced quantum-critical properties.
Theoretically, long-range interactions are extremely difficult to treat. Recently, advancements have been made in the investigation of quantum magnets with long-range interactions by primarily focusing on two Monte Carlo integration-based techniques.
The first is the technique of perturbative continuous unitary transformations, in which classical Monte Carlo integration is applied within the white graphs’ embedding scheme. This linked-cluster expansion enables the extraction of high-order series expansions of observables and energies in the thermodynamic limit. The second is the stochastic series expansion quantum Monte Carlo (SSE QMC) integration, which allows calculations on large finite systems. The infinite system's physical properties can be determined using finite-size scaling.
Both techniques have been successfully applied to two-dimensional (2D) and one-dimensional (1D) quantum magnets involving long-range Heisenberg, XY, and Ising interactions on different bipartite and non-bipartite lattices.
The SSE QMC algorithms are closely related to PI QMC algorithms and sample configurations based on the quantum mechanical Hamiltonian's Boltzmann distribution. This sampling is realized through the extension of the configuration space by operator sequences in the imaginary-time direction. The objective is to evaluate the thermal expectation values at a finite temperature for operators on a finite system.
In this paper, researchers reviewed the PI Monte Carlo techniques utilized for systems with long-range interactions.
PI QMC Algorithms
PI QMC methods that operate in continuous imaginary time have been proposed for extended Bose-Hubbard models with long-range density-density interactions, in parallel with the SSE-based QMC method development for long-range systems. In long-range interactions, the key application of these methods is the classification and determination of ground states.
Studying the Mott insulator to superfluid transition in the presence of disorder has been a major motivation for developing these PI QMC methods. Additionally, long-range density-density interactions have also been added to the algorithms.
Extended Bose-Hubbard models, which are a suitable description of ultracold molecular or atomic gases trapped within optical lattice potentials, can be effectively studied using these algorithms. In the SSE-based approach, operator sequences emerging from the exponential's high-temperature expansion in the partition function are used to extend the configuration space.
These configurations are considered as a sequence of discretely propagated states, with their position in the sequence being labeled by an artificial propagation index. This addition of an extra dimension for obtaining a configuration space sampled using Monte Carlo in the SSE and PI QMC approach indicates that both methods are closely related.
Several studies have also demonstrated the close relations between the PI and SSE representations. Hence, concepts developed within one framework can be translated with equivalence to the other framework. For instance, the concept of directed loops and loops can be used in both formulations. Thus, the Heisenberg model sampling can be transferred to the PI QMC framework as it is the directed loop concept's direct application.
In this review, researchers specifically discussed the magnetic systems’ quantum-critical properties and thus focused on the hard-core Bose-Hubbard models with dipolar density-density interactions. In this field, the PI QMC is utilized to determine the ground-state phase diagrams by studying the development of superfluid, supersolid, and solid phases.
Studies have shown that long-range interactions stabilize more solid phases than the checkerboard solid with 1/2 filling in systems with nearest-neighbor interactions. Moreover, it has also been demonstrated that long-range interactions result in the supersolid ground state emergence. The quantitative nature of QMC simulations makes these methods more advantageous compared to methods like mean-field calculations.
Thus, the numerical study of extended Bose-Hubbard models is extremely relevant as experimental progress in trapping and cooling molecules and atoms with dipolar electric/magnetic moments allows experiments to achieve extended Hubbard models with long-range interactions. The authors expect straightforward SSE QMC technique implementation for such models using the directed loop approach.
Conclusion and Future Outlook
Both unbiased and quantitative Monte Carlo integration-based approaches, including the SSE QMC approach, factor in the entire long-range interaction and can be utilized a priori for any geometry in all spatial dimensions. A large number of distinct quantum phase transitions (QPTs) are potentially accessible by these SSE QMC simulations.
The authors predict that SSE QMC, coupled with proper zero-temperature protocols and finite-size scaling, can be employed for all systems that do not suffer from a sign problem to investigate the impact of long-range interactions on QPTs beyond the standard O(n)-symmetry. Additionally, the SSE QMC approach can also be applied to study the complex crystalline phases and their breakdown in frustrated Bose-Hubbard systems with long-range interactions.
Journal Reference
Adelhardt, P., Koziol, J. A., Langheld, A., Schmidt, K. P. (2024). Monte Carlo-Based Techniques for Quantum Magnets with Long-Range Interactions. Entropy, 26(5), 401. https://doi.org/10.3390/e26050401, https://www.mdpi.com/1099-4300/26/5/401
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.
Article Revisions
- May 17 2024 - Title changed from "Monte Carlo Techniques in Quantum Magnet Research" to "Exploring Advancements in Quantum Magnetism"