In a recent article published in the journal Particles, the author demonstrated that the effective action of renormalizable quantum gravity accounts for the entropy of the present universe.
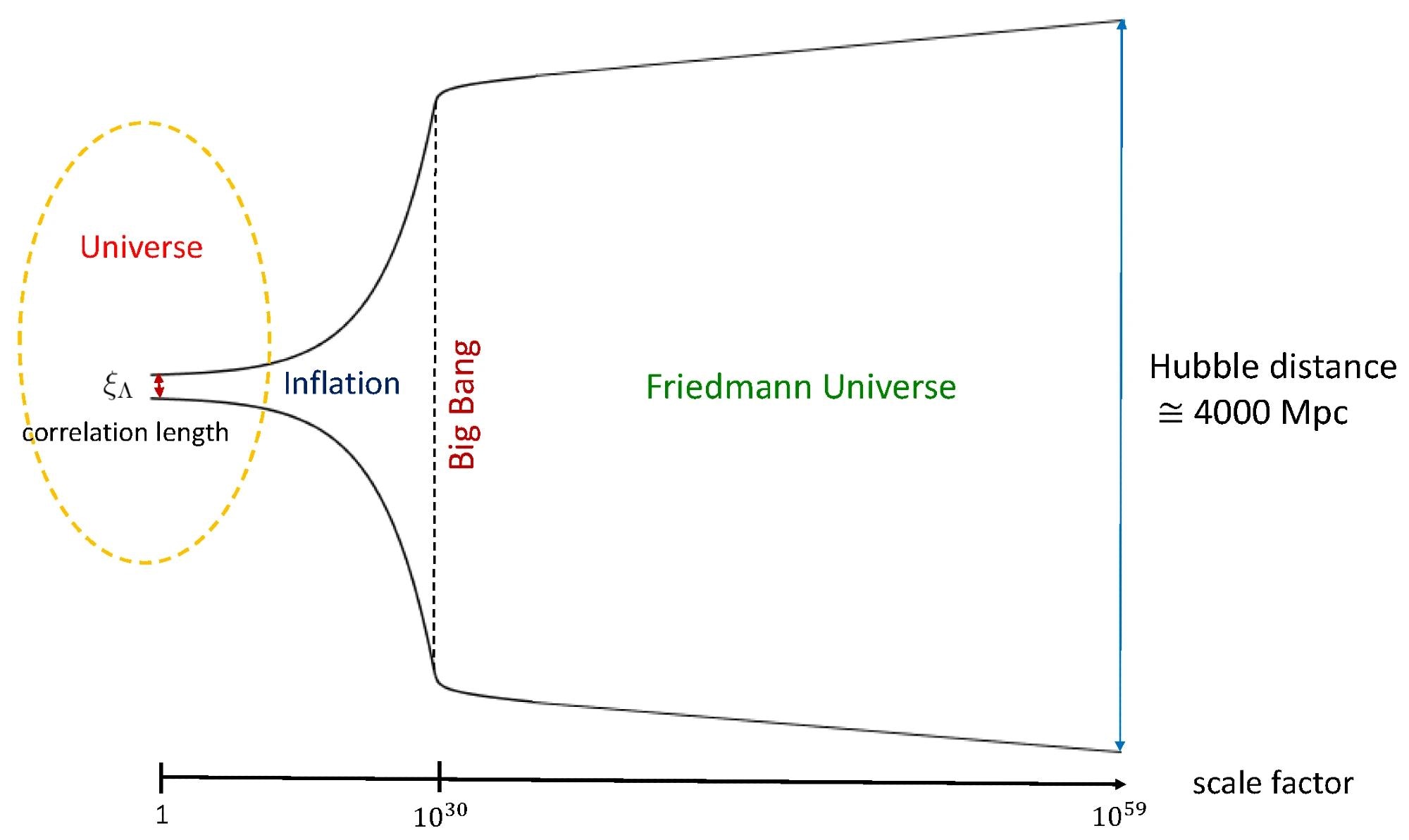 The evolution scenario of quantum gravity inflation: This shows that most of the universe we see today, represented by the Hubble distance, was originally the size of a quantum gravity excitation given by the correlation length. Image Credit: https://www.mdpi.com/2571-712X/7/2/26
The evolution scenario of quantum gravity inflation: This shows that most of the universe we see today, represented by the Hubble distance, was originally the size of a quantum gravity excitation given by the correlation length. Image Credit: https://www.mdpi.com/2571-712X/7/2/26
Entropy and the Missing Explanation
The origin of a vast amount of cosmic entropy has not been conclusively determined until now. It cannot be satisfactorily explained within the framework of Einstein's theory of gravity without introducing an unknown scalar field as the source of all matter. Furthermore, standard cosmology assumes the conservation of entropy during the universe's evolution. Although thermodynamics accounts for this conservation post-Big Bang, the sufficiency of this explanation remains uncertain.
In this work, the authors argue that the origin of entropy and its conservation law can be derived from renormalizable quantum gravity-described quantum spacetime states. Specifically, renormalizable quantum gravity that demonstrates conformal dominance at high energy beyond the Planck scale was investigated. The universe's current entropy was obtained by measuring the effective action under the quantum gravity inflation scenario caused by its dynamics.
Quantum Gravity and Effective Action
In renormalizable quantum field theory, the effective action is typically finite and renormalization group invariant. The energy-momentum tensor is also a normal product/finite and renormalization group invariant when the theory is diffeomorphism invariant.
Moreover, the entire energy-momentum tensor disappears when gravity is quantized. This fact is commonly referred to as the Hamiltonian and momentum constraints, and the Schwinger-Dyson equation provides a powerful tool to demonstrate this as a quantum-level identity.
The partition function in quantum gravity represents the sum of quantum spacetime states. The effective action, defined as the logarithm of the partition function, equates to entropy when the system’s total Hamiltonian is zero. Consequently, the effective action of quantum gravity can provide the statistical entropy of the universe's state, expressed as ΓQG = -SUniv. Here, SUniv is the entropy conserved as a renormalization group invariant. This conclusion follows from the principles of renormalizability and diffeomorphism invariance.
Ghost Modes and the Vanishing Hamiltonian
Ghost modes are essential for preserving diffeomorphism invariance and ensuring the total Hamiltonian vanishes. In Einstein's theory of gravity, a ghost mode arises due to the indefiniteness of the Einstein-Hilbert action, which permits non-trivial solutions such as the Friedmann solution. In contrast, renormalizable quantum gravity features a ghost mode as a characteristic of higher-derivative fields, even though the action itself is positive definite. In this context, the gravitational field is concealed as a sub-mode within the field and does not become a ghost.
If all modes are positive definite, a state with a vanishing Hamiltonian would be a trivial vacuum, implying no entropy. The ghost mode only poses issues when it appears as a physical particle. Renormalizable quantum gravity, which asymptotically displays background independence, addresses this ghost problem.
The theory employs an innovative perturbation technique, expanding around spacetimes where the Weyl tensor vanishes rather than around flat spacetime. The gravitational field's conformal mode, which determines distance, fluctuates non-perturbatively and is not restricted in the ultraviolet (UV) limit of this perturbation. This approach is supported by the concept of inflation.
Significance of this Work
In this work, the authors demonstrated that the universe's current entropy is derived from the effective action of renormalizable quantum gravity with asymptotic background freedom. This finding suggests that quantum gravity is the source of the universe's entropy and that it generates sufficient entropy.
Their results align with the quantum gravity inflation scenario, indicating that the universe expanded approximately 1029 times after settling into the Friedmann spacetime. Therefore, the universe must have expanded about 1030 times during the inflationary era.
Furthermore, the conservation of entropy can be derived from the principles of renormalizability and diffeomorphism invariance, which should be considered guiding principles even in the trans-Planckian regime. In the context of gravity, ghost modes, although unphysical, are necessary to provide entropy while maintaining a zero-total Hamiltonian, causing the zero-point energy to vanish.
Cosmic time, defined as a change in the central value of conformal-mode fluctuations, arises dynamically due to the presence of ghost modes. These modes also contribute to the formation of the universe's structure and are responsible for the instability of the Friedmann universe.
The study further suggests that the growth of fluctuations after the Big Bang led to the large-scale structure of the current universe. Conversely, during the inflation period, spacetime fluctuations decreased in amplitude, setting the initial conditions for the present universe. This stability is attributed to the positive definiteness of the fourth-derivative gravitational action despite the presence of ghosts as sub-modes. Thus, various ghost modes play a crucial role in the overall structure of the universe.
In summary, this study shows that the effective action of renormalizable quantum gravity effectively accounts for the present universe's entropy. However, further research is needed to understand the role of ghost modes in the quantum system of the entire universe.
Journal Reference
Hamada, K. (2024). Quantum Gravity Effective Action Provides Entropy of the Universe. Particles, 7(2), 465-476. https://doi.org/10.3390/particles7020026, https://www.mdpi.com/2571-712X/7/2/26
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.
Article Revisions
- May 16 2024 - Title changed from "Quantum Gravity and Universe's Entropy: A Revealing Connection" to "The Role of Renormalizable Quantum Gravity in Determining Cosmic Entropy"