Faster Speeds and Longer Transmission Lengths with Receiver-Dependent Key Distribution

By Skyla BailyJun 22 2022

Over the last two decades, quantum communication has advanced at a breakneck pace. The device-independent quantum key distribution (DI QKD) method has been devised, allowing remote users to create a secret in a black-box situation without relying on the precise characterization of their cryptographic hardware. This is explored extensively in the journal Quantum. 

Study: Receiver-Device-Independent Quantum Key Distribution. Image Credit: Gorodenkoff/Shutterstock.com

From a pragmatic perspective, the DI QKD idea has sparked attention, particularly as a viable solution for mitigating hacking assaults that have been experimentally proven. While the first proof-of-principle tests employing state-of-the-art settings have just been published, any practical implementation of DI QKD is still undoubtedly a long way off.

This drives research into more generic scenarios for quantum communication in which some observers or devices are trusted less. The most well-known method is Measurement-Device-Independent (MDI) QKD, in which two honest parties (Alice and Bob) submit a quantum system to a third party (Charlie) who performs a joint measurement.

The current study addresses QKD methods in a prepare-and-measure situation where the sender’s equipment is (partially) recognized while the receiver’s device can be viewed as a black box in this paper. These protocols are known as “receiver-DI”.

This technique is inspired by recent discoveries in quantum randomness generation and quantum correlations in prepare-and-measure scenarios and is based on the premise that the prepared states have limited overlaps (i.e., imposing a constraint on how distinct the states are from each other).

The method is classed as semiDI and one-sided DI, but it varies from earlier suggestions in that (i) no explicit constraint on the Hilbert space dimension of quantum systems is required, and (ii) no fair-sampling assumption is made.

Users can create a secret key in the protocols while simultaneously monitoring the quantum channel and confirming the correct operation of their devices. This verification approach for Bob’s gadget (including the communication channel) is similar to the complete DI model in that it is based solely on observable statistics.

The study reports on a proof-of-principle exercise after providing the procedures and their security analysis. With the inclusion of a high-efficiency superconducting nanowire single-photon detector (SNSPD), the configuration is basically off-the-shelf.

The protocol’s self-testing capability is demonstrated by proving that the users identify a fake decline in Bob’s detector effectiveness (as, for example, in a blinding assault).

Furthermore, it is seen that a three-state protocol can withstand greater loss than a two-state protocol, and we examine the possibilities for longer-distance implementations in general.

Methodology

Researchers consider a prepare-and-measure arrangement configuration in which Alice (sender) transmits quantum systems to Bob (receiver), who does measurements (Figure 1).

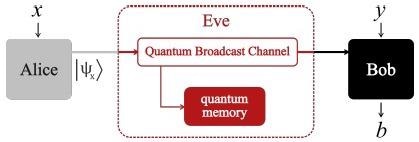
Figure 1. Scenario: Based on the observed data p (b|x, y), and the assumption that Alice’s preparations |ψ_x> have bounded overlap (see text), Alice and Bob can establish a secret key. Eve controls the quantum channel, but can also have full knowledge of the functioning of the devices of Alice and Bob. Image Credit: Ioannou, et al., 2022

The protocols’ security is ensured based on the observed statistics p (b|x, y), as determined by a lower constraint on the raw secret key rate (obtained after a post-processing step detailed below), provided that the configuration conforms to some assumptions that are explained in the study.

The study starts with some broad assumptions that apply to all QKD protocols, including the DI one. (i) Eve has no control over the state preparation x or measurement setting y options, implying that she cannot forecast these values better than at random. (ii) Except for the quantum and conventional communication defined in the protocol during the given round, no knowledge about x and y leaks to Eve. (iii) It is presumed that quantum physics is correct.

The relationship between the various states provided by Alice is a crucial assumption peculiar to the protocols.

It is assumed that their pairwise (potentially complicated) overlaps the quantum system created by Alice’s gadget. They also characterize the conditions of all systems outside of Alice’s lab if she follows the x-labeled preparation procedure.

It is worth noting that it is not necessary to identify appropriate degrees of freedom or the Hilbert space dimension of any quantum system precisely.

Only the relative distinguishability of the states counts in a broad sense. As a result, Alice’s gadget is partially characterized, but it is still susceptible to inevitable mistakes owing to technological flaws.

There is no requirement for the receiver (Bob) to characterize their equipment, and no fair sampling type assumption is employed. The methods mentioned in the study, in particular, are resistant to assaults in which Eve is in control of Bob’s equipment, which can compromise the security of typical QKD protocols.

This high level of security comes at a cost, especially the protocol’s sensitivity to losses. However, this is not a specific flaw in the protocol but rather a property of any device-independent QKD mechanism on Bob’s side (even considering a fully trusted Alice).

Indeed, Eve’s ability to launch a blinding attack places a significant restriction on the channel’s permissible broadcast.

Furthermore, Eve, in other words, interacts with each communication round independently of prior rounds, and her systems are stored in a quantum memory. With existing reduction approaches, the researchers believe that their security analysis could be extended to generic assaults.

The study proposes its simplest protocol, which is identical to the B92 protocol. Bob takes polarization measurements using two different bases. Alice and Bob will study statistics in the case of an ideal channel (lossless and noise-free).

In order to execute the last privacy amplification for distilling the secret key, Alice and Bob must bind Eve’s knowledge of the key. The channel is considered a quantum broadcast channel as seen in Figure 1 with some of the information reaching Bob’s lab and the rest being retained by Eve.

The asymptotic key rate (per round) is lower-bounded since the min-entropy lower-bounds the von Neuman entropy. The error correction cost is captured by the second term (H₂ is the binary entropy, and QBER is the quantum bit error rate).

The study demonstrates how the appropriate constraint on the key rate R behaves as a function of time in Figure 2 for protocols using n = 2, 3, 4 states of the η channel transmission.

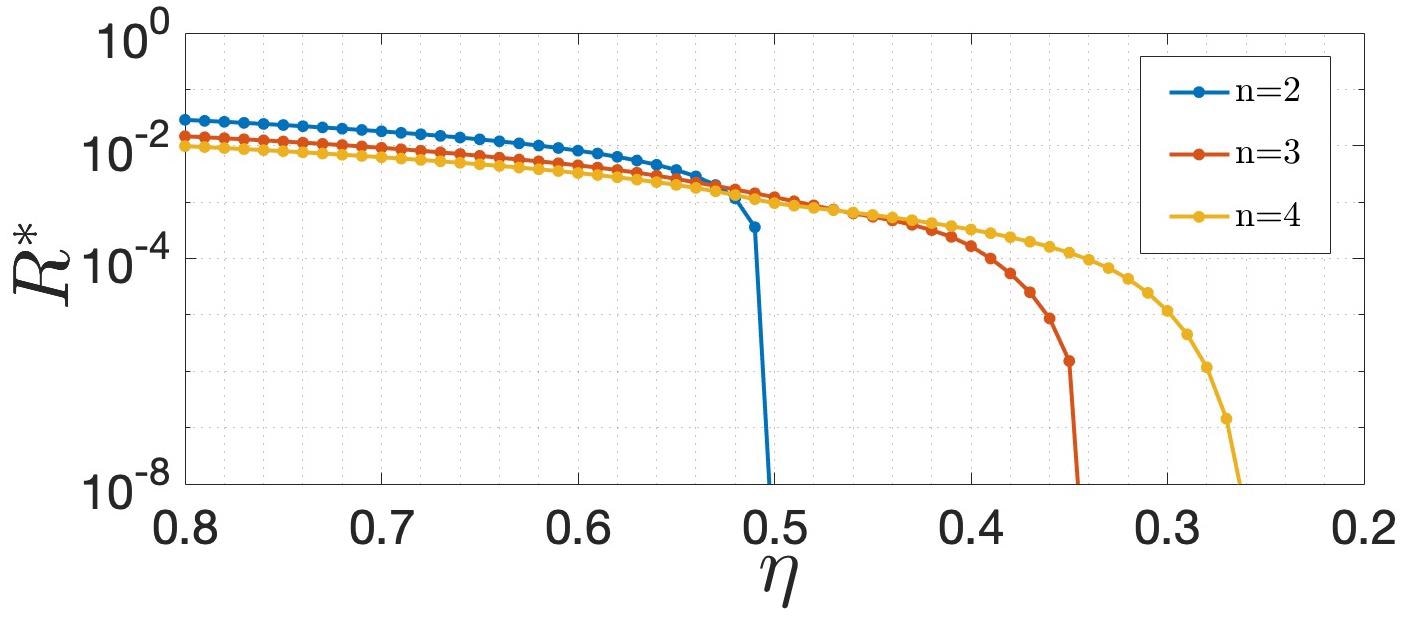
Figure 2. Lower bound, R^∗ , on the secret key rate R as a function of the transmission η. A positive key rate is obtained for transmissions down to η = 1/n, when considering a protocol where Alice prepares n states of the form in Eq. (1) (fixing the polarizations to θ = 0.2 and optimizing over the coherent state α). Image Credit: Ioannou, et al., 2022

The study assumes Alice and Bob will select their respective inputs (k, r, and y) at random. Using the approach, it becomes apparent that this issue can be reduced to a hierarchy of semi-definite programming (SDPs).

Nonetheless, the figure shows that the security approaches this barrier, indicating that by increasing the number of states n in the protocol, lower transmissions can be achieved.

Results

The quantum channel (QC), comprising Bob’s measurement setup, has a restricted loss budget, which makes experimental the execution of the protocols difficult.

Researchers employed weak coherent states stored and monitored using fibered piezo-electric polarization controllers for this feasibility experiment. Although these devices have low transmission loss, they have a speed restriction of ∼1 kHz.

Figure 3 depicts the experimental setup. A distributed feedback laser on Alice’s side generates pulses at 1559 nm with a 90 ps FWHM duration, activated at a 1 MHz rate.

A power meter is used to track the power variation of the laser output signal every second. The optical signal is then slowed down to 1 kHz using an EOM.

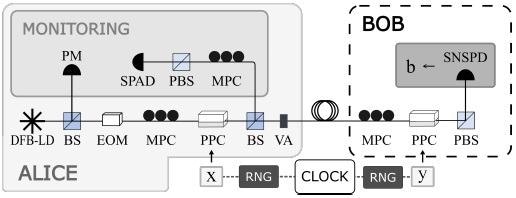
Figure 3. Experimental setup. DFB-LD: Distributed feedback laser diode; BS: Beam splitter; EOM: Electrooptic modulator; MPC: Manual polarization controller; PPC: Piezo-electric polarization controller; VA: Variable attenuator; PBS: Polarizing beam splitter; SNSPD: Superconducting nanowire single-photon detector; SPAD: Single-photon avalanche diode; PM: Powermeter; RNG: Random number generator. Image Credit: Ioannou, et al., 2022

Bob’s measurement was performed with a polarization controller that is similar to Alice’s, which allows for active selection of the measurement basis, then a PBS, and finally the SNSPD.

Using a time-to-digital converter, the detection timestamps are captured within a detection window of 1 ns. An external clock is used to activate all of the setup’s time-based components. A personal computer generates Alice’s (k, r) and Bob’s (y) inputs, which are then sent to the PPCs through Teensy microcontrollers.

The researchers initiated their study by implementing the most basic protocol with n = 2 states, examining performance as a function of QC transmission. The monitoring step allows us to measure the polarization and intensity of the light in real-time, ensuring that the overlap assumption is correct.

Researchers performed each experiment for 0.5 hours. For Alice, a random key bit k = x is created for each round, and for Bob, a random measurement setting y is generated.

Results can be seen in Figure 4. The researchers ran a finite-size Monte Carlo simulation to mimic the experiment, varying the predicted misalignment error σ between 2.5 and 4%.

​​​​​​​

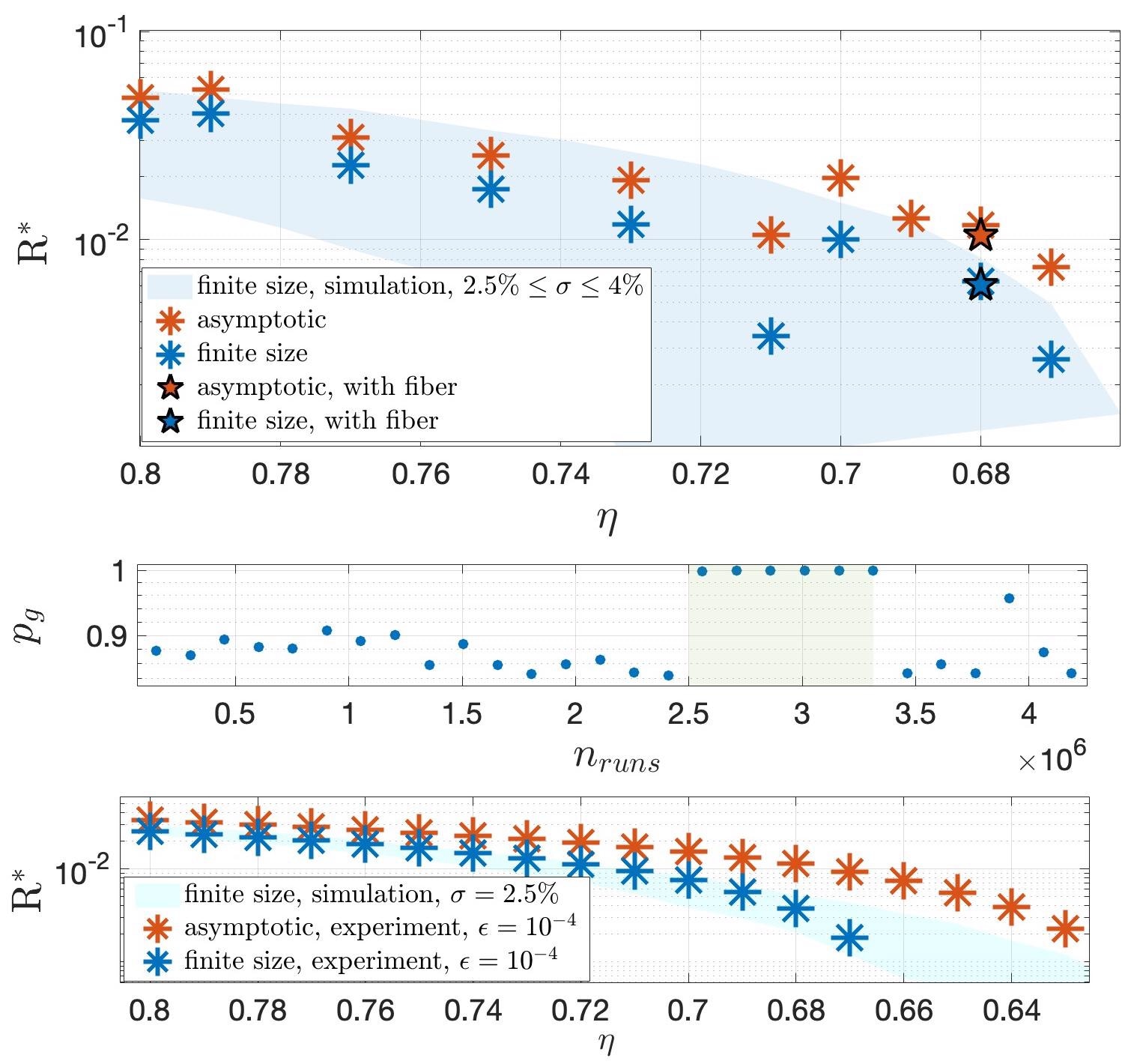
Figure 4. Experimental results. (Top) Key rate R as a function of the transmission η for the protocol with n = 2 states. Each point represents a run over half an hour, with finite-size bound on the guessing probability (blue), and in the asymptotic regime (red). Data taken with 4.8 km fiber corresponds to blue and red stars. Data is consistent with Monte Carlo simulations with polarization fluctuations 2.5% ≤ σ ≤ 4% (blue region, estimated from data). (Middle) Illustration of the self-testing feature of the protocol. After 2.5 hours of operation, we artificially lower the detection efficiency of the SNSPD (shaded region), resulting in a guessing probability pg for Eve that jumps to one, hence R = 0. Later, the SNSPD’s efficiency is brought back to normal, hence pg < 1 again and R > 0. (Bottom) Key rate R vs transmission η for the protocol with n = 3 states, showing enhanced robustness to losses. Image Credit: Ioannou, et al., 2022

The self-testing functionality of the protocol is demonstrated. The detector efficiency was purposefully lowered from 90% to 42% by reducing the SNSPD bias current. This abrupt shift is promptly identified in the post-processing, resulting in Eve’s guessing probability increasing to one.

As a result, no secret key can be deduced, and users become aware of the setup’s flaw.

Finally, the researchers implemented the protocol. They developed this technique without the random picking of parameters to reduce misalignment errors, which were caused mostly by patterning effects in the polarization controllers.

Positive key rates of η = 63% in the asymptotic domain provide enhanced resistance to loss, as seen in Figure 4.

Conclusion

In a prepare-and-measure scenario, where both parties have varying levels of confidence in their equipment, the researchers provided procedures for receiver-dependent key distribution. In comparison to the full device-independent paradigm, these protocols are far more flexible, allowing for faster speeds and longer transmission lengths.

A system based on polarization-encoded single photons, on the other hand, might be more resistant to loss. To sum up, the research establishes a new and intriguing technique in the intermediate domain between standard “device-dependent” QKD and the completely device-independent (DI) model, which is accessible to tests.

Journal Reference:

Ioannou, M., Pereira, M. A., Rusca, D., Grünenfelder, F., Boaron, A., Perrenoud, M., Abbott, A. A., Sekatski, P., Bancal, J-D., Maring, N., Zbinden, H., Brunner, N. (2022) Receiver-Device-Independent Quantum Key Distribution. Quantum, 6, p. 718. Available Online: https://quantum-journal.org/papers/q-2022-05-24-718/pdf/

References and Further Reading

1. Diamanti, E., et al. (2016) “Practical challenges in quantum key distribution”. npj Quantum Information, 2, p. 16025. doi.org/10.1038/npjqi.2016.25.
2. Xu. F., et al. (2020) “Secure quantum key distribution with realistic devices”. Reviews of Modern Physics, 92, p. 025002. doi.org/10.1103/RevModPhys.92.025002.
3. Pirandola, S., et al. (2020) “Advances in quantum cryptography”. Advances in Optics and Photonics, 12, pp. 1012–1236. doi.org/10.1364/AOP.361502.
4. Boaron., A., et al. (2018) “Secure quantum key distribution over 421 km of optical fiber”. Physical Review Letters, 121, p. 190502. doi.org/10.1103/PhysRevLett.121.190502.
5. Yin, J., et al. (2020) “Entanglement-based secure quantum cryptography over 1,120 kilometres”. Nature, 582, pp. 501–505. doi.org/10.1038/s41586-020-2401-y.
6. Chen, J.-P., et al. (2020) “Sending-or not-sending with independent lasers: Secure twin-field quantum key distribution over 509 km”. Physical Review Letters, 124, p. 070501. doi.org/10.1103/PhysRevLett.124.070501.
7. ID Quantique SA Switzerland.
8. Acín, A., et al. (2007) “Device-independent security of quantum cryptography against collective attacks”. Physical Review Letters, 98, p. 230501. doi.org/10.1103/PhysRevLett.98.230501.
9. Pironio, S., et al. (2009) “Device-independent quantum key distribution secure against collective attacks”. New Journal of Physics, 11, p. 045021.
10. Vazirani, U & Vidick T (2014) “Fully device-independent quantum key distribution”. Physical Review Letters, 113, p. 140501. doi.org/10.1103/PhysRevLett.113.140501.
11. Arnon-Friedman, R., et al. (2018) “Practical device-independent quantum cryptography via entropy accumulation”. Nature Commununication, 9, p. 459. doi.org/10.1038/s41467-017-02307-4.
12. Ekert, A & Renner, R (2014) “The ultimate physical limits of privacy”. Nature, 507, pp. 443–447. doi.org/10.1038/nature13132.
13. Lydersen, L., et al. (2010) “Hacking commercial quantum cryptography systems by tailored bright illumination”. Nature Photonics, 4, pp. 686–689. doi.org/10.1038/nphoton.2010.214.
14. Gerhardt, I., et al. (2011) “Full-field implementation of a perfect eavesdropper on a quantum cryptography system”. Nature Communication, 2, p. 349. doi.org/10.1038/ncomms1348.
15. Nadlinger, D. P., et al. (2021) “Device-independent quantum key distribution”.. doi.org/10.48550/arXiv.2109.14600.
16. Zhang, W., et al. (2021) “Experimental device-independent quantum key distribution between distant users”.. doi.org/10.48550/arXiv.2110.00575.
17. Liu., W.-Z., et al. (2021) “High-speed device-independent quantum key distribution against collective attacks”.. doi.org/10.48550/arXiv.2110.01480.
18. Lo, H.-K., et al. (2012) “Measurement-device-independent quantum key distribution”. Physical Review Letters, 108, p. 130503. doi.org/10.1103/PhysRevLett.108.130503.
19. Samuel L., et al. (2012) “Side-channel-free quantum key distribution”. Physical Review Letters, 108, p. 130502. doi.org/10.1103/PhysRevLett.108.130502.
20. Tomamichel, M & Renner, R (2011) “Uncertainty relation for smooth entropies”. Physical Review Letters, 106, p. 110506. doi.org/10.1103/PhysRevLett.106.110506.
21. Tomamichel, M., et al. (2012) “Tight finite-key analysis for quantum cryptography”. Nature Communications, 3, p. 634. doi.org/10.1038/ncomms1631.
22. Tomamichel, M & Leverrier, A (2017) “A largely self-contained and complete security proof for quantum key distribution”. Quantum, 1, p. 14. doi.org/10.22331/q-2017-07-14-14.
23. Acín, A., et al. (2016) “Necessary detection efficiencies for secure quantum key distribution and bound randomness”. Physical Review A, 93, p. 012319. doi.org/10.1103/PhysRevA.93.012319.
24. Branciard, C., et al. (2012) “One-sided deviceindependent quantum key distribution: Security, feasibility, and the connection with steering”. Physical Review A, 85, p. 010301. doi.org/10.1103/PhysRevA.85.010301.
25. Brask, J. B., et al. (2017) “Megahertz-rate semi-deviceindependent quantum random number generators based on unambiguous state discrimination”. Physical Review Applied, 7, p. 054018. doi.org/10.1103/PhysRevApplied.7.054018.
26. Van Himbeeck, T., et al. (2017) “Semidevice-independent framework based on natural physical assumptions”. Quantum, 1, p. 33. doi.org/10.22331/q-2017-11-18-33.
27. Rusca, D., et al. (2019) “Practical self-testing quantum random number generator based on a energy bound”. Physical Review A, 100, p. 062338. doi.org/10.1103/PhysRevA.100.062338.
28. Wang, Y., et al. (2019) “Characterising the correlations of prepare-and-measure quantum networks”. npj Quantum Information, 5, p. 17. doi.org/10.1038/s41534-019-0133-3.
29.  Pawłowski M & N Brunner (2011) “Semi-device independent security of one-way quantum key distribution”. Physical Review A, 84, p. 010302(R). doi.org/10.1103/PhysRevA.84.010302.
30. Woodhead, E & Pironio, S (2015) “Secrecy in prepare-and-measure clauser-horneshimony-holt tests with a qubit bound”. Physical Review Letters, 115, p. 150501. doi.org/10.1103/PhysRevLett.115.150501.
31. Ma, X & Lutkenhaus, N (2011) “Improved data post-processing in quantum key distribution and application to loss thresholds in device independent qkd”. Quantum Information and Computation, 12, p. 3. doi.org/10.48550/arXiv.1109.1203.
32. Ho, M., et al. (2020) “Noisy preprocessing facilitates a photonic realization of device-independent quantum key distribution”. Physical Review Letters, 124, p. 230502. doi.org/10.1103/PhysRevLett.124.230502.
33. Schwonnek, R., et al. (2021) “Device-independent quantum key distribution with random key basis”. Nature Communication, 12, p. 2880. doi.org/10.1038/s41467-021-23147-3.
34. Woodhead, E., et al. (2021) “Device-independent quantum key distribution with asymmetric CHSH inequalities”. Quantum, 5, p. 443. doi.org/10.22331/q-2021-04-26-443.
35. Sekatski, P., et al. (2021) “Deviceindependent quantum key distribution from generalized CHSH inequalities”. Quantum, 5, p. 444. doi.org/10.22331/q-2021-04-26-444.
36. Renner, R (2007) “Symmetry of large physical systems implies independence of subsystems”. Nature Physics, 3, pp. 645–649. doi.org/10.1038/nphys684.
37. Dupuis, F., et al. (2020) “Entropy accumulation”. Communications in Mathematical Physics, 379, pp. 867–913. doi.org/10.1007/s00220-020-03839-5.
38. Charles H & Bennett (1992) “Quantum cryptography using any two nonorthogonal states”. Physical Review Letters, 68, pp. 3121–3124. doi.org/10.1103/PhysRevLett.68.3121.
39. Ioannou, M., et al. (2021) Abbott, Denis Rosset, Jean-Daniel Bancal, and Nicolas Brunner. “Receiver-device independent quantum key distribution protocols”. arXiv:2110.00575. doi.org/10.48550/arXiv.2110.00575.
40. Devetak, I & Winter, A (2005) “Distillation of secret key and entanglement from quantum states”. Proceedings of the Royal Society, A461, pp. 207–235. doi.org/10.1098/rspa.2004.1372.
41. Fawzi, H., et al. (2018) “Semidefinite approximations of the matrix logarithm”. Foundations of Computational Mathematics, 19, p. 259. doi.org/10.1007/s10208-018-9385-0.
42. Grünenfelder, F., et al. (2020) “Performance and security of 5 ghz repetition rate polarization-based quantum key distribution”. Applied Physics Letters, 117, p. 144003. doi.org/10.1063/5.0021468.
43. Charnes, A & Cooper, W. W (1962) “Programming with linear fractional functionals”. Naval Research logistics quarterly, 9, pp. 181–186. https://doi.org/10.1002/nav.3800090303.
44. Lin, P.-S., et al. (2018) “Device-independent point estimation from finite data and its application to deviceindependent property estimation”. Physical Review A, 97, p. 032309. doi.org/10.1103/PhysRevA.97.032309.
45. Bancal, J. D., et al. (2021) “Self-testing with finite statistics enabling the certification of a quantum network link”. Quantum, 5, p. 401. doi.org/10.22331/q-2021-03-02-401.