Demonstration of Circuit Simulation-Specific Compiler Passes

By Skyla BailyJun 14 2022

Although quantum circuits are prepared for execution on quantum hardware, quantum computing frameworks also allow for the simulation of algorithms on classical computers. Researchers, in the journal Quantum, proposed an innovative circuit simulation-specific compiler pass. These findings show that collaborating on circuit compiler and simulator development and integration is useful and cuts simulation time in half.

Study: Fast simulation of quantum algorithms using circuit optimization. Image Credit: Yurchanka Siarhei/Shutterstock.com

Quantum computation has recently made the transition from scientific research to technology development. The development of more complex software frameworks to allow the execution of algorithms on actual quantum devices has been one of the most noticeable advances.

The compiler, sometimes known as a transpiler, mapper, or scheduler, depending on its function, is a key component of frameworks. The compiler must convert an abstract algorithm into instructions that can be executed by the quantum devices' electrical controller.

Simulators can be used for at least two main functions. On the one hand, they allow quantum algorithms to be benchmarked without the limits of conventional hardware, such as finite coherence time. Simulators, on the other hand, when equipped with realistic noise models, may help characterize hardware noise and decoherence and, in certain cases, provide information about its source.

Notably, the ProjectQ compiler permits multi-qubit operations in algorithm descriptions without requiring them to be decomposed into 1- and 2-qubit gates, which is useful for simulation because multi-qubit gates are not inherent in most quantum hardware. Researchers provide a novel compiler pass for decreasing the simulation time for arbitrary quantum circuits in this paper.

Researchers improve the Intel Quantum Simulator (IQS), a high-performance simulator with multi-threading and distributed parallelization, by adding a customizable mechanism to express the quantum state as a distributed vector.

It is simple to imagine that qubits used to communicate between chips differ from qubits utilized within the device, therefore the optimization distinction of local/global qubits might be altered to correspond to qubits for computing/communicating. The concept of a quantum chip network is both a part of company roadmaps and the starting point for recent research and open-source software.

It is worth noting that an effective optimizing pass for gate fusion requires the inclusion of multi-qubit gates in the circuit’s intermediate representation. Furthermore, with a hybrid Schrödinger-Feynman simulator developed by NASA, a tensor network-based simulator developed by Alibaba, or by leveraging secondary storage as analyzed by IBM, ad-hoc circuit manipulation has been used to simulate exactly the sort of random circuits proposed by Google for quantum supremacy.

When scientists discuss compiler-simulator co-development, researchers are referring to this shift in perspective.

Researchers compare the time to simulate random circuits with and without the suggested compiler pass to evaluate the ability of the specific improvement discussed in this paper. The number of gates needing inter-node communication is reduced by one order of magnitude when the ratio of 1- and 2-qubit gates in the circuits is changed. As a result, the entire simulation time is often cut in half.

Methodology

IQS is a cutting-edge Schrödinger simulator that stores all 2ⁿ complex amplitudes of n qubits to reflect their whole state. All quantum circuit activities, such as state preparation and many 1- and 2-qubit gates, are implemented as linear amplitude manipulation. Because the 2-qubit gate known as CNOT is included in this set, IQS may imitate any circuit (arbitrary 1-qubit gates and CNOT allow universal quantum computation).

The time taken to replicate 1- and 2-qubit gates as a function of the number of qubits involved is shown in Figure 1.

Figure 1. Simulations of n = 35 qubits using 128 MPI processes, each running on one node of Frontera supercomputer. Each process uses 24 OpenMP threads. (Top) Time to execute a 1-qubit gate as a function of the qubit involved. When the gate is executed on qubit with index m = n – [log₂ k] (with k being the number of MPI processes), the communication between the MPI tasks is happening between sockets of the same node. For qubits with index larger than m, communication is between distinct nodes. (Bottom) Time to execute a 2-qubit gate as a function of the involved qubits. CNOT is the controlled Pauli X gate. Image Credit: Guerreschi, et al., 2022

The simulations were done on the Texas Advanced Computing Center’s Frontera supercomputer, which has two sockets of Intel^® Xeon^® Processor 8280 CPUs on each computing node (24 cores per socket).

To improve the representation of quantum states in IQS, researchers add the new function PermuteQubits 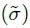. Researchers propose a compiler pass that runs over every quantum circuit and adds qubit-reordering instructions to remove communication costs from most gates.

Results

Researchers assess the time it takes to simulate random circuits before and after optimization to quantify the benefit offered by the compiler pass. Random circuits of the following type are considered: fix the number of gates; each gate has a probability p of being a 2-qubit gate; otherwise, it is a 1-qubit gate with probability of 1 - p. In the sets {H, Y}, and {CNOT} for 1- and 2-qubit gates, the exact kind of gate is chosen uniformly at random.

Random circuits are also typical of methods like the Quantum Approximate Optimization Algorithm for solving combinatorial problems on a class of random instances or the dynamical development of spin systems with random interactions, which are not connected with a specific application.

In the first experiment, the number of qubits is fixed at n = 35, and the probability p is varied. Figure 2 shows the findings, which were obtained by averaging 20 random circuits of (30 n) gates on n = 35 qubits.

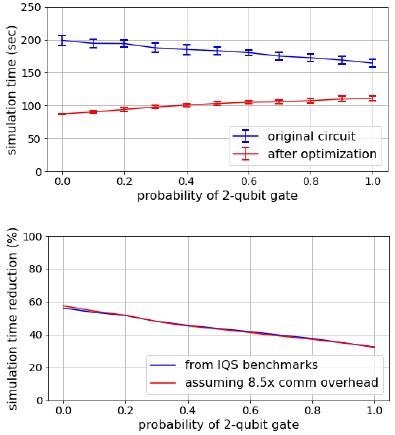
Figure 2. Effect of the compiler pass to optimize quantum circuits for simulation with IQS. (Top) Simulation time of random circuits of 1050 gates on n = 35 qubits. The timings have been estimated for the same configuration used in Figure 1: 128 computing nodes of Frontera supercomputer at TACC. There are m = 28 local qubits. Data points represent the average over 20 random circuits and the vertical bars indicate one standard deviation. (Bottom) Reduction of the simulation time between original and optimized circuit. The blue line is based on direct benchmarks of IQS, the red line is obtained by assuming that operations requiring communication have an overhead of 8.5× with respect to operations implementable locally. This overhead is in line with the benchmarks in Figure 1. Image Credit: Guerreschi, et al., 2022

The simulation time was calculated by adding the time necessary to simulate each gate individually. Experts begin by comparing the performance of each type of gate on each qubit or pair of qubits.

Figure 3 shows the number of communication overhead gates (which includes qubit reordering operations) as a percentage of the total number of original operations.

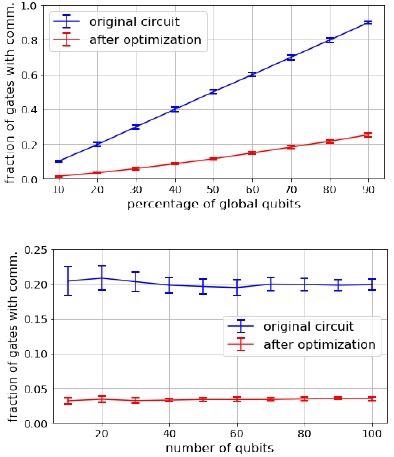
Figure 3. Effect of the compiler pass to optimize quantum circuits for simulation with IQS. Fraction of gates requiring communication for the original (blue) and optimized (red) circuit. (Top) Fixing n = 50, we vary the percentage of global qubits from 10% to 90%. (Bottom) Fixing the ratio global vs. total qubits to 1:5, we vary n. In both panels, data points are averaged over 20 random circuits and the vertical bars indicate one standard deviation. The random circuit have (30 n) gates. Image Credit: Guerreschi, et al., 2022

The controlled-Rz gates are replaced with CNOT gates in QFTlike circuits (QFT stands for Quantum Fourier Transform). The reason for the replacement is because controlled-Rz gates have a diagonal computational base and do not require communication, but CNOT gates do, as seen in Figure 1. The circuits are constructed as shown in Figure 4 below.

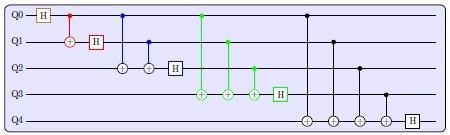
Figure 4. Quantum circuit with the same structure as the Quantum Fourier Transform circuit, but with CNOT gates substituting controlled-Rz rotations. Image Credit: Guerreschi, et al., 2022

The number of gates needing communication may be calculated as a function of the number of qubits n and the proportion of local qubits m/n using the simple qubit ordering in which low-index qubits are local and high-index qubits are global.

Furthermore, it is clear that just 2(n-m) qubit permutations are required to remove all communication overhead (two permutations for each of the same-color gates with Hadamard on a global qubit). The pass researchers suggest this is very successful for QFT-like circuits, as shown in Figure 5.

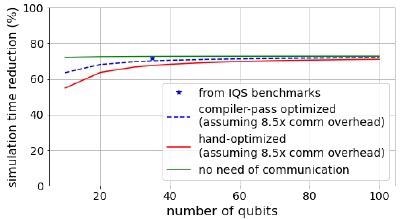
Figure 5. Effect of the compiler pass to optimize QFT-like quantum circuits for simulation with IQS. The blue star uses the benchmark results from Figure 1, while the dashed blue line uses a simplified model in which operations requiring communication have an overhead of 8. 5x with respect to operations implementable locally (see caption of Figure 2). The green line represents the limiting case in which no operation would require communication. For all circuit sizes, it has been assumed that 20% of the qubits are global. Image Credit: Guerreschi, et al., 2022

Conclusion

On the one hand, researchers extended Intel Quantum Simulator, a high-performance, distributed, and open-source simulator, to versatile data structures and qubit reordering features; on the other hand, researchers proposed a novel compiler pass based on reducing the number of operations requiring communication between computing nodes. Scientists believe that circuit simulation-specific compiler passes will become an essential component of quantum computation systems.

Journal Reference:

Guerreschi, G.G., 2022. Fast simulation of quantum algorithms using circuit optimization. Quantum, 6, p.706. Available Online: https://quantum-journal.org/papers/q-2022-05-03-706/

References and Further Reading

1. Alexander S., et al. (2013) Quipper: A scalable quantum programming language. Proceedings PLDI, 13 (48), pp. 333–342. doi.org/10.1145/2491956.2462177.
2. David Wecker & Krysta, M. S (2014) LIQUi|>: A Software Design Architecture and Domain-Specific Language for Quantum Computing. Quantum Physics (quant-ph), arXiv:1402.4467. doi.org/10.48550/arXiv.1402.4467.
3. Damian S. S., et al. (2018) ProjectQ: An Open Source Software Framework for Quantum Computing'. Quantum, 2, p. 49. doi.org/10.22331/q-2018-01-31-49.
4. The Qiskit Contributors. (2019) Qiskit: An open-source framework for quantum computing. Qiskit / qiskit. Available at: https://github.com/Qiskit/qiskit
5. The Cirq Contributors. Cirq, a python framework for creating, editing, and invoking noisy intermediate scale quantum (NISQ) circuits. Quantumlib / Cirq. Available at: https://github.com/quantumlib/Cirq
6. Robert S. S., et al. (2016) A practical quantum instruction set architecture. Quantum Physics (quant-ph). doi.org/10.48550/arXiv.1608.03355.
7. Nathan, K., et al. (2019) Strawberry Fields: A Software Platform for Photonic Quantum Computing. Quantum, 3, p. 129. doi.org/10.22331/q-2019-03-11-129.
8. The Orquestra Contributors. Build and deploy quantum-ready applications^® on the Orquestra^® platform. In: Orquestra^® platform. Available at: https:// www.zapatacomputing.com/orquestra/.
9. The Braket Contributors. Amazon Bracket - Accelerate quantum computing research. In: Quantum Technologies. https://aws.amazon.com/braket/
10. Ali, J., et al. (2014) ScaffCC: A framework for compilation and analysis of quantum computing programs'. In: CF '14 Proceedings of the 11th ACM Conference on Computing Frontiers, 1. doi.org/10.1145/2597917.2597939.
11. Cowtan, A., et al. (2019) On the qubit routing problem. In: Leibniz International Proceedings in Informatics, LIPIcs, 135, pp. 5:1–5:32. doi.org/10.4230/LIPIcs.TQC.2019.5.
12. Childs, A. M., et al. (2019) Circuit transformations for quantum architectures. In: Leibniz International Proceedings in Informatics, LIPIcs, 135, pp. 1–24. doi.org/10.4230/LIPIcs.TQC.2019.3.
13. Almudever, C. G., et al. (2020) Realizing Quantum Algorithms on Real Quantum Computing Devices. In: 2020 Design, Automation and Test in Europe Conference and Exhibition, DATE, pp. 864–872. doi.org/10.23919/DATE48585.2020.9116240.
14. Smelyanskiy, M., et al. (2016) qHiPSTER: The quantum high performance software testing environment. Quantum Physics (quant-ph). arXiv:1601.07195. doi.org/10.48550/arXiv.1601.07195.
15. Pednault, E., et al. (2017) Breaking the 49-qubit barrier in the simulation of quantum circuits. Quantum Physics (quant-ph). arXiv:1710.05867. doi.org/10.48550/arXiv.1710.05867.
16. Raedt, H. D., et al. (2019) Massively parallel quantum computer simulator, eleven years later. Computer Physics Communications, 237, pp. 47–61. doi.org/10.1016/j.cpc.2018.11.005.
17. Häner, T & Steiger, D S (2017) 0.5 petabyte simulation of a 45-qubit quantum circuit. In: International Conference for High Performance Computing, Networking, Storage and Analysis, SC 17, 33, pp. 1–10. doi.org/10.1145/3126908.3126947.
18. Khammassi, N., et al. (2017) QX: A high-performance quantum computer simulation platform. Design, Automation & Test in Europe Conference & Exhibition (DATE), 2017. doi.org/10.23919/date.2017.7927034.
19. Jones, T., et al. (2019) QuEST and high performance simulation of quantum computers. Scientific Reports, 9, p. 10736. doi.org/10.1038/s41598-019-47174-9.
20. The Huawei HiQ Team. Huawei hiq: A high-performance quantum computing simulator and programming framework. Available at: http:// hiq.huaweicloud.com
21. Villalonga, B., et al. (2020) Establishing the quantum supremacy frontier with a 281 Pflop/s simulation. Quantum Science and Technology, 5(3), p. 034003. doi.org/10.1088/2058-9565/ab7eeb.
22. O'Brien, T. E., et al. (2017) Density-matrix simulation of small surface codes under current and projected experimental noise. npj Quantum Information, 3, p. 39. doi.org/10.1038/s41534-017-0039-x.
23. Villalonga, B., et al. (2019) A flexible high-performance simulator for verifying and benchmarking quantum circuits implemented on real hardware. npj Quantum Information, 5, p. 86. doi.org/10.1038/s41534-019-0196-1.
24. Häner, T., et al. (2018) A Software Methodology for Compiling Quantum Programs. Quantum Science and Technology, 3(2), p. 020501. doi.org/10.1088/2058-9565/aaa5cc.
25. Guerreschi, G. G., et al. (2020) Intel Quantum Simulator: A cloud-ready high-performance simulator of quantum circuits. Quantum Science and Technology, 5(3), p. 034007. doi.org/10.1088/2058-9565/ab8505.
26. Chapman, P (2020) Scaling IonQ's Quantum Computers: The Roadmap. In: IONQ. Available at: https:// ionq.com/posts/december-09-2020-scaling-quantum-computer-roadmap/.
27. Rodrigo, S., et al. (2021) Scaling of multi-core quantum architectures. In: CF '21: 18th ACM International Conference on Computing Frontiers, pp. 144–151. doi.org/10.1145/3457388.3458674
28. Häner, T., et al. (2021) Distributed Quantum Computing with QMPI. In: SC '21: International Conference for High Performance Computing, Networking, Storage and Analysis, 16, pp. 1–13. doi.org/10.1145/3458817.3476172.
29. Diadamo, S., et al. (2021) QuNetSim: A Software Framework for Quantum Networks. IEEE Transactions on Quantum Engineering, 2, p. 2502512. doi.org/10.1109/TQE.2021.3092395.
30. Dahlberg, A & Wehner, S (2019) SimulaQron - A simulator for developing quantum internet software. Quantum Science and Technology, 4(1), p. 015001. doi.org/10.1088/2058-9565/aad56e.
31. Raedt, K. D., et al. (2007) Massively parallel quantum computer simulator. Computer Physics Communications, 176(2), pp. 121–136. doi.org/10.1016/j.cpc.2006.08.007.
32. Suzuki, Y., et al. (2021) Qulacs: a fast and versatile quantum circuit simulator for research purpose. Quantum, 5, p. 559. doi.org/10.22331/q-2021-10-06-559.
33. Arute, F., et al. (2019) Quantum supremacy using a programmable superconducting processor. Nature, 574, pp. 505–510. doi.org/10.1038/s41586-019-1666-5.
34. Huang, C., et al. (2020) Classical Simulation of Quantum Supremacy Circuits. Quantum Physics (quant-ph). doi.org/10.48550/arXiv.2005.06787.
35. Pednault, E., et al. (2019) Leveraging Secondary Storage to Simulate Deep 54-qubit Sycamore Circuits. Quantum Physics (quant-ph). doi.org/10.48550/arXiv.1910.09534.
36. Luo, X-Z., et al. (2020) Yao.jl: Extensible, Efficient Framework for Quantum Algorithm Design. Quantum, 4, p. 341. doi.org/10.22331/q-2020-10-11-341.
37. Guerreschi, G G & Park, J (2018) Two-step approach to scheduling quantum circuits. Quantum Science and Technology, 3(4), p. 045003. doi.org/10.1088/2058-9565/aacf0b.
38. Lao, L., et al. (2022) Timing and Resource-Aware Mapping of Quantum Circuits to Superconducting Processors. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 41(2), pp. 359–371. doi.org/10.1109/TCAD.2021.3057583.
39. Itoko, T., et al. (2020) Optimization of quantum circuit mapping using gate transformation and commutation. Integration, 70, pp. 43–50. doi.org/10.1016/j.vlsi.2019.10.004.
40. Sivarajah, S., et al. (2021) t|ket⟩: A Retargetable Compiler for NISQ Devices. Quantum Science and Technology, 6(1), p. 014003. doi.org/10.1088/2058-9565/ab8e92.
41. Farhi, E., et al. (2014) A quantum approximate optimization algorithm. Quantum Physics (quant-ph). doi.org/10.48550/arXiv.1411.4028.
42. Salathé, Y., et al. (2015) Digital quantum simulation of spin models with circuit quantum electrodynamics. Physical Review X, 5, p. 021027 (2015). doi.org/10.1103/PhysRevX.5.021027.