Analysis of an Enhanced Critical Quantum Metrology Technique

By Skyla BailyMay 30 2022

Quantum metrology is a framework for enhancing measurement precision beyond the normal quantum limit by employing quantum-mechanical factors such as non-classical correlations and quantum entanglement. A study in the journal Quantum considers a novel advanced critical quantum metrology technique.

Study: Understanding and Improving Critical Metrology. Quenching Superradiant Light-Matter Systems Beyond the Critical Point. Image Credit: Yershov Oleksandr/Shutterstock.com

One of the most quickly expanding and evolving fields of physics is the control and manipulation of light-matter interactions. The coupling of a cavity field to an atom gas—quantum-gas cavity with quantum electrodynamics is of special importance because the interaction between light and matter is substantially amplified by the light that passes through the same atomic system several times. 

Moreover, due to non-classical correlations and the possibility of non-destructive observation of these systems using photons escaping from cavity mirrors, they provide an excellent platform for exact measurements of unknown physical properties beyond the usual quantum limit. As a result, quantum-gas cavity quantum electrodynamics systems may pave the way for new quantum metrology paradigms.

In theory, leveraging N-body interactions might result in an exponential increase in attainable accuracy; nevertheless, such interactions have been suggested to be unphysical.

Although metrological systems like the ones outlined can theoretically be utilized to attain the Heisenberg limit, they are frequently exceedingly difficult to test. As a result, Heisenberg-limited metrology is now limited to proof-of-concept experiments with systems containing only a few constituents, such as atoms or photons.

Finally, in some instances, the precise measurement necessary to saturate the Cramér-Rao constraint may not be attainable; for example, the best measurement may equate to a projection onto a heavily entangled state.

The so-called critical quantum metrology, which has received a lot of interest in recent years, is a good example of concurrently imprinting data about an unknown parameter while establishing quantum correlations. Critical quantum metrology takes use of the quantum state’s extraordinary sensitivity to disturbances when it is close to a quantum phase transition.

If the Hamiltonian displays a quantum phase transition at x_c, the critical quantum metrology technique may be used to adiabatically drive the system to this critical point and make an appropriate measurement providing a large Fisher information.

This shows that, with the system only having two-body interactions, an exponential increase in Fisher information may be observed not just in time but also in practice with N. In finite-component systems, the exponential expansion of quantum Fisher information is also evident (thus finite-component quantum phase transitions).

Quenching over a transition also avoids the problem of critical slowing down that might occur when preparing states at a critical point, as shown in Figure 1.

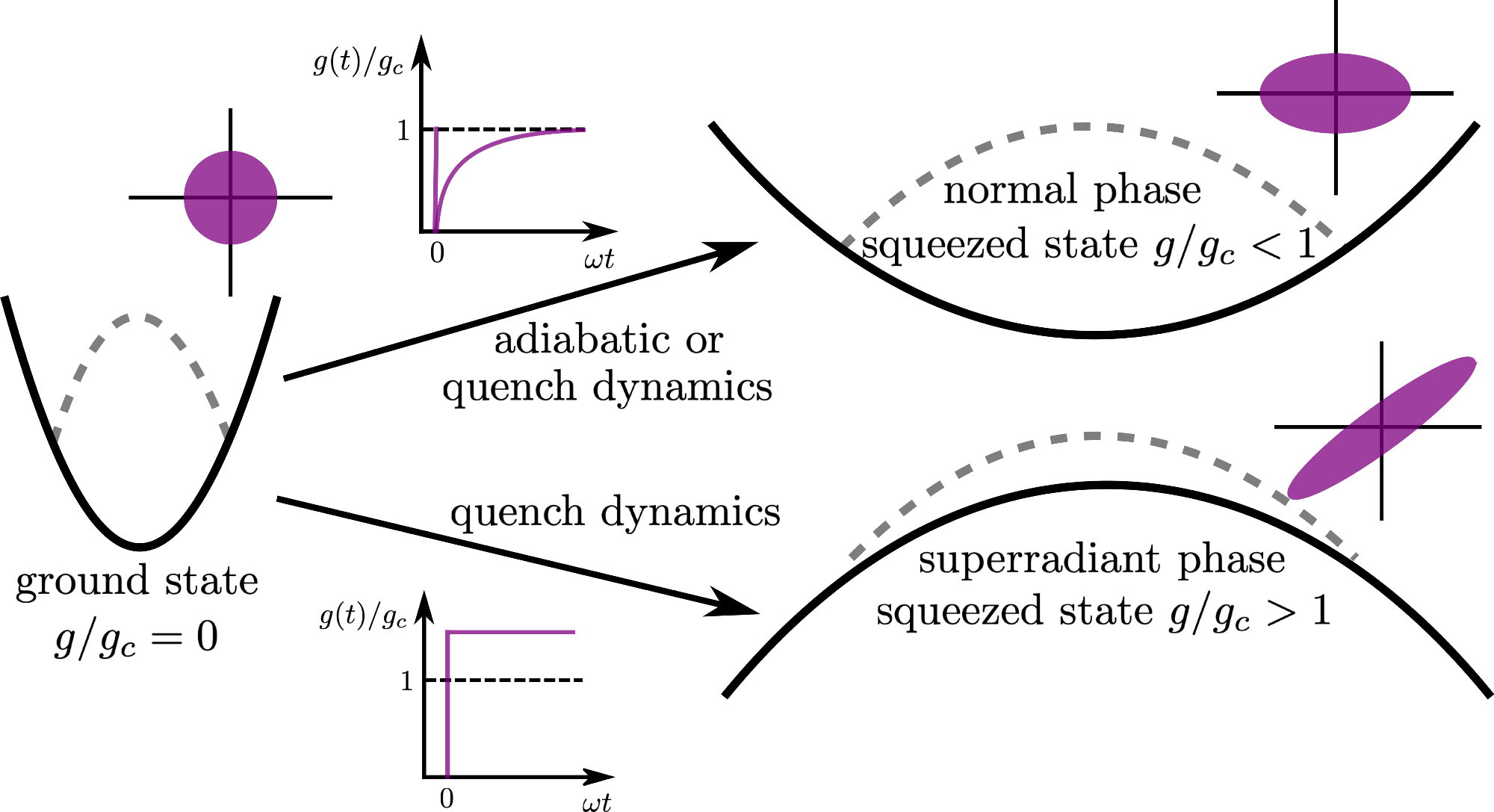
Figure 1. The schematic represents a toy model for a quantum phase transition (g/g_c > 1 is the superradiant phase), with the black line being the effective potential that is felt by a quantum state (dashed-gray line). Driving the system close to the critical point (g/gc ∼ 1) creates the correlated (squeezed) excitations at a very slow rate (critical slowing down), since the effective potential is still of trapping form. However, if the system is quenched beyond the critical point (g/g_c > 1), the same number of correlated excitations can be generated much faster since the initial state will behave as if it was placed in an inverted harmonic oscillator potential. The purple ellipses represent the phase space picture of the state. Image Credit: Gietka, et al., 2022

Methodology

Superradiant quantum phase transitions are a common occurrence in quantum optics, occurring when a group of two-level systems (usual atoms) interacts with a single quantum state oscillator with a harmonic component (electromagnetic field). The superradiant phase is defined by a large number of excitations (photons) in the medium.

We can consider the Dicke model to see how the metrology approach makes use of the superradiant phase transition. This well-liked design is known that the interaction of N two-level particles with a single-mode field exhibits a phase transition from superradiant to non-radiant.

The spectrum, including the critical ground state and consequently the quantum Fisher information, may be calculated analytically using this effective model. 

Researchers recreate an altered Dicke Hamiltonian in order to shed some insight on the system dynamics. However, it appears that pushing beyond the critical point may result in divergence on ever shorter time periods of quantum Fisher information.

In the superradiant regime, the analytical findings illustrating the evolution of the quantum Fisher information as a result of the coupling parameter and time are shown in Figure 2 and Figure 3.

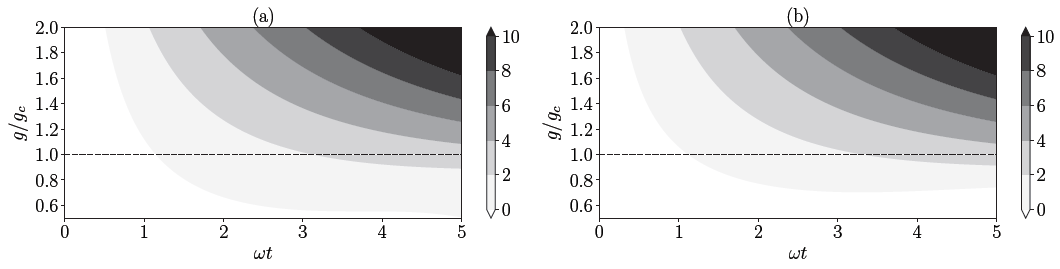
Figure 2. The logarithm of the quantum Fisher information (for initial vacuum state) normalized to λ² as a function of g/g_c and time expressed in the units of ω⁻¹. Panel (a) and (b) depict the quantum Fisher information for λ = ω and λ = Ω, respectively. The dashed line illustrates the quantum Fisher information attainable by quenching the system to the critical point. Image Credit: Gietka, et al., 2022

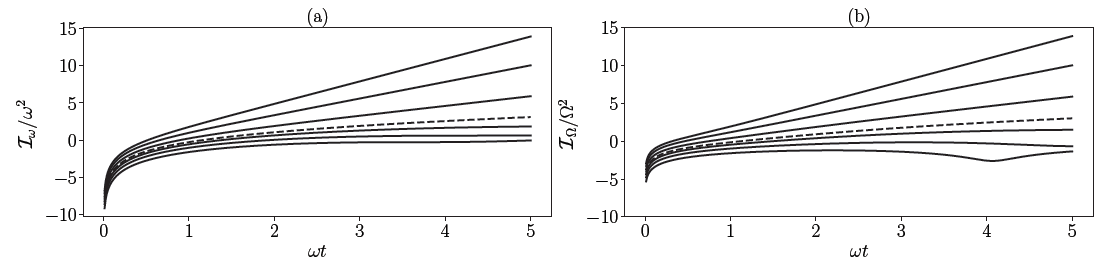
Figure 3. Extension of Figure 2 showing slices of the logarithm of the quantum Fisher information for different values of g/g_c (from the bottom line 0.5, 0.68, 0.87, 1, 1.25, 1.62, 2). The dashed line represents g/g_c = 1. Image Credit: Gietka, et al., 2022

Figure 4 shows the analytical findings comparing quantum and classical Fisher information for quadrature measurement as a function of quadrature angle φ and time for g = √2g_c.

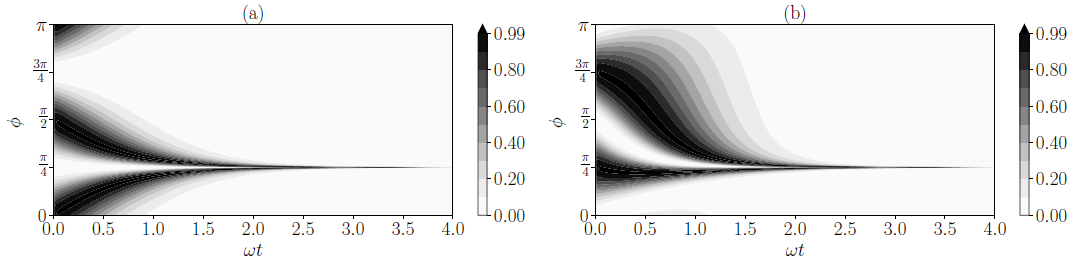
Figure 4. Classical Fisher information for quadrature measurement as a function of quadrature direction φ and time expressed in units of ω normalized to the quantum Fisher information. The calculations are performed for g/gc ≈ √2 which corresponds to the generation of a perfectly squeezed vacuum in Eq. (10). We plot 0 < φ < π as the information is invariant under rotation by π. Panel (a) treats ω as the unknown parameter and panel (b) treats Ω as the unknown parameter. In both cases the optimal quadrature direction converges to π/4. Image Credit: Gietka, et al., 2022

Any uncertainty in such an apparatus—in this example, the observed quadrature angle’s possible instability—will have a direct impact on estimate precision, as seen in Figure 5.

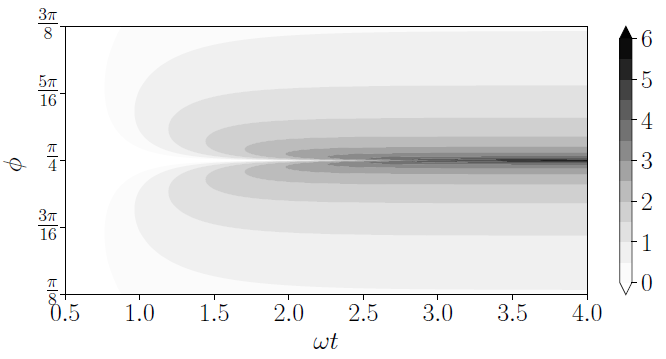
Figure 5. Logarithm of the classical Fisher information from Eq. (19) (multiplied by ω²). As the classical Fisher information grows, the angle-window for the optimal quadrature direction becomes smaller and converges to a single point (here π/4). Result for g = √2g_c. Image Credit: Gietka, et al., 2022

Researchers ran simulations to illustrate the saturation of the Cramér-Rao constraint for different values of g/g_c, and the results are shown in Figure 6. As a function of φ and time, the picture illustrates classical Fisher information normalized to quantum Fisher information.

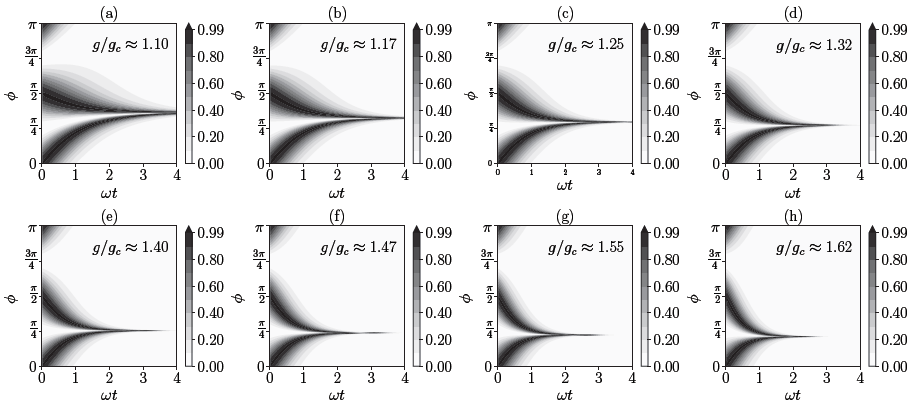
Figure 6. Classical Fisher information normalized to the quantum Fisher information as a function of φ and time for various values of g/g_c. In all the cases the homodyne detection in the optimal direction saturates the Cramér-Rao bound. Image Credit: Gietka, et al., 2022

Result

Even if the condition may not always be satisfied, and detection of squeezing may be impossible owing to spontaneous symmetry breakdown, the exponential development of the Fisher information should still be an observable effect in experimental realizations of the Dicke model in cavity systems.

This is due to the fact that, even in the mean-field method, the exponential expansion of the number of photons preceding the dynamical phase transition (superradiance) happens for a wide range of parameters.

In general, because the spin dynamics will not be frozen, the analytical description of the system will be more obtuse than the elegant formalism with an inverted harmonic oscillator; however, the information about the unknown parameter should still be imprinted in the number of photons that grows exponentially in time.

Conclusion

To overcome the critical slowing down that inhibits critical quantum metrology protocols, researchers suggest quenching the system well past the critical point, hence increasing the rate at which correlations are formed. The proposed method is substantially quicker (i.e., exponential vs power-law time scaling) than current adiabatic and dynamical protocols, which might be critical in practical circumstances where decoherence and experimental noise are unavoidable.

Researchers have argued and demonstrated theoretically that the quadrature measurement can saturate the quantum Cramér-Rao constraint for an appropriate angle outside of the normal phase because quenching the system into the superradiant phase yields a Gaussian state.

Quantum simulators that achieve the (optical) quantum Rabi model and quantum simulators that can realize the (optical) Dicke model, i.e. a macroscopic number of spins linked to a single-mode field, can easily test our procedure.

A gas of atoms in an optical cavity, as detailed in this paper, is a viable possibility. Furthermore, researchers have demonstrated that the sensitivity of these systems may expand exponentially with the square root of the number of atoms N, showing that exponential scaling Fisher information can be a physical and measurable phenomenon that does not require an N-body term.

The proposed concept opens the way for metrology methods that can benefit from storing unknown parameter information in the number of excitations. Testing the suggested protocol in quantum simulators that simulate the Dicke (Rabi) model without photonic degrees of freedom is an exciting prospect. This finding suggests that merely monitoring system excitations, such as center-of-mass excitations in a spin-orbit linked Bose-Einstein condensate, might improve metrology.

Journal Reference

Gietka, K., Ruks, L. and Busch, T. (2022) Understanding and Improving Critical Metrology. Quenching Superradiant Light-Matter Systems Beyond the Critical Point. Quantum, 6, p.700. Available Online: https://quantum-journal.org/papers/q-2022-04-27-700/

References and Further Reading

1. Hammerer, K., et al. (2010) Quantum interface between light and atomic ensembles, Reviews of Modern Physics, 82, p. 1041. doi.org/10.1103/RevModPhys.82.1041.
2. Ritsch, H., et al. (2013) Cold atoms in cavity-generated dynamical optical potentials, Reviews of Modern Physics, 85, p. 553. doi.org/10.1103/RevModPhys.85.553.
3. Mivehvar, F., et al. (2021) Cavity QED with quantum gases: new paradigms in many-body physics, Advances in Physics, 70, p. 1. doi.org/10.1080/00018732.2021.1969727.
4. Vitali, D., et al. (2007) A cavity-QED scheme for Heisenberg-limited interferometry, Journal of Modern Optics, 54, p. 1551. doi.org/10.1080/09500340600741124.
5. Gammelmark, S & Mølmer, K (2011) Phase transitions and Heisenberg limited metrology in an Ising chain interacting with a single-mode cavity field, New Journal of Physics, 13, p. 053035. doi.org/10.1088/1367-2630/13/5/053035.
6. Liu, Z. P., et al. (2016) Metrology with PT -Symmetric Cavities: Enhanced Sensitivity near the PT -Phase Transition, Physical Review Letters, 117, p. 110802. doi.org/10.1103/PhysRevLett.117.110802.
7. Gietka, K., et al. (2017) Quantum-enhanced interferometry with cavity QED-generated non-classical light, European Physical Journal D, 71, p. 273. doi.org/10.1140/epjd/e2017-80235-2.
8. Cheng, W., et al. (2019) Quantum metrology enhanced by coherence-induced driving in a cavity-QED setup, Physical Review A, 100, p. 053825. doi.org/10.1103/PhysRevA.100.053825.
9. Gietka, K., et al. (2019) Supersolid-Based Gravimeter in a Ring Cavity, Physical Review Letters, 122, p. 190801. doi.org/10.1103/PhysRevLett.122.190801.
10. Lewis-Swan, R. J., et al. (2020) Protocol for Precise Field Sensing in the Optical Domain with Cold Atoms in a Cavity, Physical Review Letters, 124, p. 193602. doi.org/10.1103/PhysRevLett.124.193602.
11. Gietka, K., et al. (2021a) Cavity-enhanced magnetometer with a spinor Bose–Einstein condensate, New Journal of Physics, 23, p. 043020. doi.org/10.1088/1367-2630/abedff.
12. Chu, A., et al. (2021a) Quantum Enhanced Cavity QED Interferometer with Partially Delocalized Atoms in Lattices, Physical Review Letters, 127, p. 210401. doi.org/10.1103/PhysRevLett.127.210401.
13. Giovannetti, V., et al. (2004) Quantum-enhanced measurements: beating the standard quantum limit, Science, 306, p. 1330. doi.org/10.1126/science.1104149.
14.  Giovannetti, V., et al. (2006) Quantum Metrology, Physical Review Letters, 96, p. 010401. doi.org/10.1103/PhysRevLett.96.010401.
15. Pinel, O., et al. (2013) Quantum parameter estimation using general single-mode Gaussian states, Physical Review A, 88, p. 040102. doi.org/10.1103/PhysRevA.88.040102.
16. Pezzé, L & Smerzi, A (2009) Entanglement, Nonlinear Dynamics, and the Heisenberg Limit, Physical Review Letters, 102, p. 100401. doi.org/10.1103/PhysRevLett.102.100401.
17. Boixo, S., et al. (2007) Generalized Limits for Single-Parameter Quantum Estimation, Physical Review Letters, 98, p. 090401. doi.org/10.1103/PhysRevLett.98.090401.
18. Braunstein, S L & Caves, C M (1994) Statistical distance and the geometry of quantum states, Physical Review Letters, 72, p. 3439. doi.org/10.1103/PhysRevLett.72.3439.
19. Pezzè, L., et al. (2018) Quantum metrology with nonclassical states of atomic ensembles, Reviews of Modern Physics, 90, p. 035005. doi.org/10.1103/RevModPhys.90.035005.
20. Polino, E., et al. (2020) Photonic quantum metrology, AVS Quantum Science, 2, p. 024703. doi.org/10.1116/5.0007577.
21. Pang, S & Jordan, A N (2017) Optimal adaptive control for quantum metrology with time-dependent Hamiltonians, Nature Communications, 8, p. 14695. doi.org/10.1038/ncomms14695.
22. Hou, Z., et al. (2021) ``super-Heisenberg'' and Heisenberg Scalings Achieved Simultaneously in the Estimation of a Rotating Field, Physical Review Letters, 126, p. 070503. doi.org/10.1103/PhysRevLett.126.070503.
23. Roy, S M & Braunstein, S L (2008) Exponentially Enhanced Quantum Metrology, Physical Review Letters, 100, p. 220501. doi.org/10.1103/PhysRevLett.100.220501.
24. Marciniak, C. D., et al. (2022) Optimal metrology with programmable quantum sensors, Nature, 603, p. 604. doi.org/10.1038/s41586-022-04435-4.
25. Rossi, M. A. C., et al. (2020) Noisy Quantum Metrology Enhanced by Continuous Nondemolition Measurement, Physical Review Letters, 125, p. 200505. doi.org/10.1103/PhysRevLett.125.200505.
26. Gietka, K., et al. (2021b) Adiabatic critical quantum metrology cannot reach the Heisenberg limit even when shortcuts to adiabaticity are applied, Quantum, 5, p. 489. doi.org/10.22331/q-2021-07-01-489.
27. Braun, D., et al. (2018) Quantum-enhanced measurements without entanglement, Reviews of Modern Physics, 90, p. 035006. doi.org/10.1103/RevModPhys.90.035006.
28. Zanardi, P., et al. (2008) Quantum criticality as a resource for quantum estimation, Physical Review A, 78, p. 042105. doi.org/10.1103/PhysRevA.78.042105.
29. Invernizzi, C., et al. (2008) Optimal quantum estimation in spin systems at criticality, Physical Review A, 78, p. 042106. doi.org/10.1103/PhysRevA.78.042106.
30. Ivanov, P A & Porras, D (2013) Adiabatic quantum metrology with strongly correlated quantum optical systems, Physical Review A, 88, p. 023803. doi.org/10.1103/PhysRevA.88.023803.
31. Tsang, M (2013) Quantum transition-edge detectors, Physical Review A, 88, p. 021801. doi.org/10.1103/PhysRevA.88.021801.
32. Salvatori, G., et al. (2014) Paris, Quantum metrology in Lipkin-Meshkov-Glick critical systems, Physical Review A, 90, p. 022111. https://doi.org/10.1103/PhysRevA.90.022111.
33. Macieszczak, K., et al. (2016) Dynamical phase transitions as a resource for quantum enhanced metrology, Physical Review A, 93, p. 022103. doi.org/10.1103/PhysRevA.93.022103.
34. Bina, M., et al. (2016) Dicke coupling by feasible local measurements at the superradiant quantum phase transition, Physical Review E, 93, p. 052118. doi.org/10.1103/PhysRevE.93.052118.
35. Fernández-Lorenzo, S & Porras, D (2017) Quantum sensing close to a dissipative phase transition: Symmetry breaking and criticality as metrological resources, Physical Review A, 96, p. 013817. doi.org/10.1103/PhysRevA.96.013817.
36. Heugel, T. L., et al. (2019) Quantum Transducer Using a Parametric Driven-Dissipative Phase Transition, Physical Review Letters, 123, p. 173601. doi.org/10.1103/PhysRevLett.123.173601.
37. Garbe, L., et al. (2020) Critical Quantum Metrology with a Finite-Component Quantum Phase Transition, Physical Review Letters, 124, p. 120504. doi.org/10.1103/PhysRevLett.124.120504.
38. Salado-Mejía, M., et al. (2021) Moya-Cessa, Spectroscopy and critical quantum thermometry in the ultrastrong coupling regime, Quantum Science and Technology, 6, p. 025010. doi.org/10.1088/2058-9565/abdca5.
39. Hatomura, T., et al. (2022) Quantum metrology based on symmetry-protected adiabatic transformation: imperfection, finite time duration, and dephasing, New Journal of Physics, 24, p. 033005. doi.org/10.1088/1367-2630/ac5375.
40. Ilias, T., et al. (2022) Criticality-Enhanced Quantum Sensing via Continuous Measurement, PRX Quantum, 3, p. 010354. doi.org/10.1103/PRXQuantum.3.010354.
41. Garbe, L., et al. (2021) Critical Quantum Metrology with Fully-Connected Models: From Heisenberg to Kibble-Zurek Scaling, pp. 2110–04144. doi.org/10.48550/arXiv.2110.04144.
42. Gietka, K (2021) Squeezing by Critical Speeding-up: Applications in Quantum Metrology, pp. 2111–12206. doi.org/10.48550/arXiv.2111.12206.
43. Sachdev, S (2007) Quantum phase transitions, Handbook of Magnetism and Advanced Magnetic Materials. doi.org/10.1002/9780470022184.
44. You, W. L., et al. (2007) Fidelity, dynamic structure factor, and susceptibility in critical phenomena, Physical Review E, 76, p. 022101. doi.org/10.1103/PhysRevE.76.022101.
45. Born, M & Fock, V (1928) Beweis des Adiabatensatzes, Zeitschrift für Physik, 51, p. 165. doi.org/10.1007/BF01343193.
46. Rams, M. M., et al. (2018) At the Limits of Criticality-Based Quantum Metrology: Apparent Super-Heisenberg Scaling Revisited, Physical Review X, 8, p. 021022. doi.org/10.1103/PhysRevX.8.021022.
47. Chu, Y., et al. (2021b) Dynamic Framework for Criticality-Enhanced Quantum Sensing, Physical Review Letter, 126, p. 010502. doi.org/10.1103/PhysRevLett.126.010502.
48. Gietka, K & Busch, T (2021) Inverted harmonic oscillator dynamics of the nonequilibrium phase transition in the Dicke model, Physical Review E, 104, p. 034132. doi.org/10.1103/PhysRevE.104.034132.
49. Perarnau-Llobet, M., et al. (2021) Weakly invasive metrology: quantum advantage and physical implementations, Quantum, 5, p. 446. doi.org/10.22331/q-2021-04-28-446.
50. Felicetti, S & Le Boité, A (2020) Universal Spectral Features of Ultrastrongly Coupled Systems, Physical Review Letter, 124, p. 040404. doi.org/10.1103/PhysRevLett.124.040404.
51. Larson, J & Irish, E. K (2017) Some remarks on `superradiant' phase transitions in light-matter systems, Journal of Physics A: Mathematical, 50, p. 174002. doi.org/10.1088/1751-8121/aa65dc.
52. Peng, J., et al. (2019) Unified superradiant phase transitions, Physical Review A, 100, p. 063820. doi.org/10.1103/PhysRevA.100.063820.
53. Hwang, M. J., et al. (2015) Quantum Phase Transition and Universal Dynamics in the Rabi Model, Physical Review Letter, 115, p. 180404. doi.org/10.1103/PhysRevLett.115.180404.
54. Bravyi, S., et al. (2011) Schrieffer–Wolff transformation for quantum many-body systems, Annals of Physics, 326, p. 2793. doi.org/10.1016/j.aop.2011.06.004.
55. Weedbrook, C., et al. (2012) Gaussian quantum information, Reviews of Modern Physics, 84, p. 621. doi.org/10.1103/RevModPhys.84.621.
56. Walls, D F (1983) Squeezed states of light, Nature, 306, p. 141. https://doi.org/10.1038/306141a0.
57. Pang, S & Brun, T A (2014) Quantum metrology for a general Hamiltonian parameter, Physical Review A, 90, p. 022117. doi.org/10.1103/PhysRevA.90.022117.
58. Monras, A (2006) Optimal phase measurements with pure Gaussian states, Physical Review A, 73, p. 033821. doi.org/10.1103/PhysRevA.73.033821.
59. Oh, C., et al. (2019) Optimal Gaussian measurements for phase estimation in single-mode Gaussian metrology, npj Quantum Information, 5, p. 10. doi.org/10.1038/s41534-019-0124-4.
60. Berni, A. A. et al. (2015) Ab initio quantum-enhanced optical phase estimation using real-time feedback control, Nature Photonics, 9, p. 577. doi.org/10.1038/nphoton.2015.139.
61. Wiseman, H M & Milburn, G J (2009) Quantum Measurement and Control (Cambridge University Press). doi.org/10.1017/CBO9780511813948.
62. Hentschel, A & Sanders, B C (2011) Efficient Algorithm for Optimizing Adaptive Quantum Metrology Processes, Physical Review Letter, 107, p. 233601. doi.org/10.1103/PhysRevLett.107.233601.
63. Demkowicz-Dobrzański, R., et al. (2017) Adaptive Quantum Metrology under General Markovian Noise, Physical Review X, 7, p. 041009. doi.org/10.1103/PhysRevX.7.041009.
64.  Pezzè, L & Smerzi, A (2021) Quantum Phase Estimation Algorithm with Gaussian Spin States, PRX Quantum, 2, p. 040301. doi.org/10.1103/PRXQuantum.2.040301.
65. Šafránek, D (2018) Estimation of Gaussian quantum states, Journal of Physics A: Mathematical, 52, p. 035304. doi.org/10.1088/1751-8121/aaf068.
66. Bakmou, L., et al. (2020) Multiparameter quantum estimation theory in quantum Gaussian states, Journal of Physics A: Mathematical, 53, p. 385301. doi.org/10.1088/1751-8121/aba770.
67. Black, A. T., et al. (2003) Observation of Collective Friction Forces due to Spatial Self-Organization of Atoms: From Rayleigh to Bragg Scattering, Physical Review Letter, 91, p. 203001. doi.org/10.1103/PhysRevLett.91.203001.
68. Baumann, K., et al. (2010) Dicke quantum phase transition with a superfluid gas in an optical cavity, Nature, 464, p. 1301. doi.org/10.1038/nature09009.
69. Nagy, D., et al. (2010) Dicke-Model Phase Transition in the Quantum Motion of a Bose-Einstein Condensate in an Optical Cavity, Physical Review Letter, 104, p. 130401. doi.org/10.1103/PhysRevLett.104.130401.
70. Domokos, P & Ritsch, H (2002) Collective Cooling and Self-Organization of Atoms in a Cavity, Physical Review Letter, 89, p. 253003. doi.org/10.1103/PhysRevLett.89.253003.
71. Klinder, J., et al. (2015) Dynamical phase transition in the open Dicke model, Proceedings of the National Academy of Sciences of the United States of America, 112, p. 3290. doi.org/10.1073/pnas.1417132112.
72. Baden, M. P., et al. (2014) Realization of the Dicke Model Using Cavity-Assisted Raman Transitions, Physical Review Letter, 113, p. 020408. doi.org/10.1103/PhysRevLett.113.020408.
73. Kroeze, R. M., et al. (2018) Spinor Self-Ordering of a Quantum Gas in a Cavity, Physical Review Letter, 121, p. 163601. doi.org/10.1103/PhysRevLett.121.163601.
74. Keßler, H., et al. (2021) Hemmerich, Observation of a Dissipative Time Crystal, Physical Review Letter, 127, p. 043602. doi.org/10.1103/PhysRevLett.127.043602.
75. Dareau, A., et al. (2018) Observation of Ultrastrong Spin-Motion Coupling for Cold Atoms in Optical Microtraps, Physical Review Letter, 121, p. 253603. doi.org/10.1103/PhysRevLett.121.253603.
76. Forn-Díaz, P., et al. (2019) Ultrastrong coupling regimes of light-matter interaction, Reviews of Modern Physics, 91, p. 025005. doi.org/10.1103/RevModPhys.91.025005.
77. Kockum, A. F., et al. (2019) Ultrastrong coupling between light and matter, Nature Reviews Physics, 1, p. 19. doi.org/10.1038/s42254-018-0006-2.
78. Hamner, C., et al. (2014) Dicke-type phase transition in a spin-orbit-coupled Bose–Einstein condensate, Nature Communications, 5, p. 4023. doi.org/10.1038/ncomms5023.
79. Safavi-Naini, A., et al. (2018) Verification of a Many-Ion Simulator of the Dicke Model Through Slow Quenches across a Phase Transition, Physical Review Letter, 121, p. 040503. doi.org/10.1103/PhysRevLett.121.040503.
80. Gambetta, F. M., et al. (2019) Exploring nonequilibrium phases of the generalized Dicke model with a trapped Rydberg-ion quantum simulator, Physical Review A, 100, p. 022513. doi.org/10.1103/PhysRevA.100.022513.
81. Yunusova, K. M., et al. (2019) Coupling between Rydberg States and Landau levels of Electrons Trapped on Liquid Helium, Physical Review Letter, 122, p. 176802. https://doi.org/10.1103/PhysRevLett.122.176802.
82. Krämer, S., et al. (2018) QuantumOptics.jl: A Julia framework for simulating open quantum systems, Computer Physics Communications, 227, p. 109. doi.org/10.1016/j.cpc.2018.02.004.