Editorial Feature

Eigenstate Entanglement in Collective Spin Integrable Models

Jun 22 2022

While the correlation between degrees of freedom and constants of motion is widely recognized in classical mechanics, a truly comprehensive and robust definition of integrability for quantum systems remains unclear. This has been explored recently in a study in the journal Quantum. 

Study: Eigenstate entanglement in integrable collective spin models. Image Credit: Andrew Derr/Shutterstock.com

The presence of an optimal solution of the model, like the Bethe ansatz based on the Yang-Baxter equation, or other properties, including a set of simple conserved quantities or Poissonian level statistics, are frequently connected with quantum integrability.

None of these characteristics, on the other hand, provides a clear characterization of integrable quantum systems that differentiates them from nonintegrable quantum systems. Since the primary purpose is to characterize quantum dynamics, a suitable metric or measure should be able to accurately divide all quantum models into two categories: integrable and nonintegrable, each with radically different dynamical behavior.

Quantum entanglement can be a defining measure for integrability in quantum theory with a tensor product structure. Various studies have found a direct link between entanglement and dynamical properties.

The qualitative characteristic of the spread of entanglement in many types of spin systems is a good illustration. There are integrable and non-integrable chains, many-body localized systems or quantum scars, as well as additional models like the Dicke model.

Another way to investigate this link is to look into entanglement in energy eigenstates and how it affects quantum dynamics.

Researchers also look at the entanglement pattern over the eigenstates, which goes beyond the average entanglement entropy (EE). Researchers discover that, based on the parameters, it exhibits a range of structures, including singular spots that correlate to singularities in the density of states. Considering these disparate EE distributions, it is worth noting that the average EE always converges to the same number.

Discussion

Normalized average entanglement for the complete Dicke basis and the basis consisting of an equal superposition of conjugate Dicke states as a function of 1/Smax(= 1/ log(N/2 + 1)) at half bipartition. The linear fits correspond to a + b/Smax with intercept a fixed to 1/2. N ? [104, 6 × 104] for the Dicke basis, and [4 × 103, 2.8 × 104] for the superposition basis for the shown data points. Inset shows log (1 - R2), where R2 is the coefficient of determination of the linear fit, for different fixed values of the intercept a. At a = 1/2, the values of (1-R2) are 10-10 and 10-5 for the Dicke basis and the superposition basis, respectively.

Figure 1. Normalized average entanglement for the complete Dicke basis and the basis consisting of an equal superposition of conjugate Dicke states as a function of 1/Smax(≡ 1/ log(N/2 + 1)) at half bipartition. The linear fits correspond to a + b/Smax with intercept a fixed to 1/2. N ∈ [104, 6 × 104] for the Dicke basis, and [4 × 103, 2.8 × 104] for the superposition basis for the shown data points. Inset shows log (1 − R2), where R2 is the coefficient of determination of the linear fit, for different fixed values of the intercept a. At a = 1/2, the values of (1−R2) are 10−10 and 10−5 for the Dicke basis and the superposition basis, respectively. Image Credit: Kumari & Alhambra, 2022

The EE’s values are far from optimal. Subsystems of permutation-symmetric multi-qubit systems are also permutation-symmetric, and thus their local Hilbert space dimension is permutation-symmetric.

Researchers can show that at the thermodynamic limit, the average EE over Dicke states coincides with exactly half of the maximum feasible EE.

This form of entanglement scaling is substantially slower than that seen in generic states across the entire Hilbert space, where the entanglement entropy might reach SA = NA log 2. Researchers are now looking at the numerical behavior of normalized average EE convergence over Dicke basis in the thermodynamic limit.

The possibility of recognizing integrable collective spin models utilizing average EE in vanishing bipartitions is controlled because the thermodynamic limits of the 1-qubit average EE do not correlate for two distinct bases, which are both eigenbases of the integrable LMG model for a particular choice of parameters.

Researchers now provide the major result on the LMG model’s average EE: that in the thermodynamic limit, the uniform normalized average of the half bipartition EE of all eigenstates converges to a fixed value of 1/2, regardless of parameter choice. 

(a) Normalized average entanglement S¯A Smax at half bipartition p = 1/2, as a function of the inverse maximal entanglement 1/Smax = 1/ log(N/2 + 1), given parameters (?x ?y h) in the LMG model. The linear fits correspond to a + b/Smax with intercept a fixed to be 1/2. The inset shows a zoomed-in version of the linear fit. (b) The plot of log(1-R2 ) for all the parameter sets in (a), when the intercept a is fixed at different values in [0.48, 0.52]. Here, R2 is the coefficient of determination of the linear fit for different intercept values. For a = 1/2, (1-R2 ) varies between 10-3 and 10-6. The number of qubits N ? [2×103, 104 ] for the data points in this figure, and the average EE are over the eigenstates from only the positive parity sector of Rp z. Also, the eigenbasis of HLMG for (?x ?y h) = (0, 0, -1) plotted here is the Dicke basis.

Figure 2. (a) Normalized average entanglement 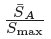 at half bipartition p = 1/2, as a function of the inverse maximal entanglement 1/Smax = 1/ log(N/2 + 1), given parameters (γx γy h) in the LMG model. The linear fits correspond to a + b/Smax with intercept a fixed to be 1/2. The inset shows a zoomed-in version of the linear fit. (b) The plot of log(1−R2) for all the parameter sets in (a), when the intercept a is fixed at different values in [0.48, 0.52]. Here, R2 is the coefficient of determination of the linear fit for different intercept values. For a = 1/2, (1−R2) varies between 10−3 and 10−6. The number of qubits N ∈ [2×103, 104] for the data points in this figure, and the average EE are over the eigenstates from only the positive parity sector of Rzπ. Also, the eigenbasis of HLMG for (γx γy h) = (0, 0, −1) plotted here is the Dicke basis. Image Credit: Kumari & Alhambra, 2022

Related Stories

The results are depicted in Figure 2(a), where the normalized average EE declines as the system size is larger, and finite-size scaling reveals that it always hits a thermodynamic limit value of 1/2.

This is supported by Figure 2(b)’s examination of the coefficient of determination, which measures the fit quality. Researchers can observe that when the intercept is fixed at 1/2, the best linear fits happen. The figures show the outcomes for a range of N qubits up to 104.

Researchers also conducted a numerical investigation for another bipartition. They confirm this with the findings in Figure 3, where they plot the average EE as a function of the subsystem size p for N = 213 and discover an almost linear development reliable with a fixed ratio.

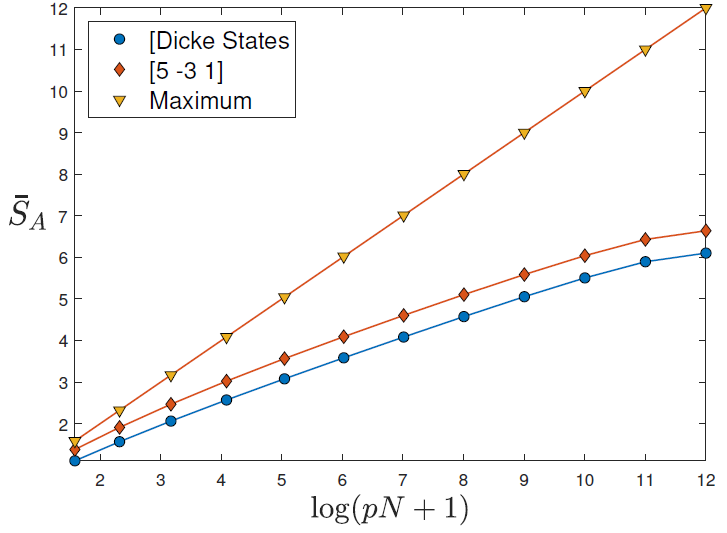
The plot of the average EE for different bipartitions p = NA/N, of the eigenstates in the LMG model corresponding to (?x, ?y, h) = (5, -3, 1) and for the Dicke basis. The maximum EE in the given bipartition is also plotted for comparison. N = 8192 (= 2 13) for this plot. Up to close to the half bipartition p = 1/2, all the curves are roughly straight lines.

Figure 3. The plot of the average EE for different bipartitions p = NA/N, of the eigenstates in the LMG model corresponding to (γx, γy, h) = (5, −3, 1) and for the Dicke basis. The maximum EE in the given bipartition is also plotted for comparison. N = 8192 (≡ 213) for this plot. Up to close to the half bipartition p = 1/2, all the curves are roughly straight lines. Image Credit: Kumari & Alhambra, 2022

Researchers analyze the entanglement distribution in the spectrum, plotted in Figure 4, to better understand the applicability of the average EE. To truly comprehend the characteristics of this distribution, researchers also investigate the properties of the LMG model. Singularities (logarithmic divergences) and discontinuities can be found in the LMG model’s density of states (DOS).

Distribution of entanglement entropy at half-bipartition for all the eigenstates of the LMG model in the positive parity sector, as a function of their eigenenergy. Zones 1 to 4 corresponds to the choice of four sets of parameters (?x, ?y, h) = (1/2, 1/3, 1), (2, 1/2, 1), (5, -3, 1), and (5, 3, 1) in the model. There are dips in the entanglement distribution at eigenenergies corresponding to the singularities in the density of states. For this plot, we have N = 104.

Figure 4. Distribution of entanglement entropy at half-bipartition for all the eigenstates of the LMG model in the positive parity sector, as a function of their eigenenergy. Zones 1 to 4 corresponds to the choice of four sets of parameters (γx, γy, h) = (1/2, 1/3, 1), (2, 1/2, 1), (5, −3, 1), and (5, 3, 1) in the model. There are dips in the entanglement distribution at eigenenergies corresponding to the singularities in the density of states. For this plot, we have N = 104. Image Credit: Kumari & Alhambra, 2022

Conclusion

The entanglement entropy in the eigenstates of a collective spin integrable model, the LMG model, was investigated. The average EE in non-vanishing bipartitions accumulates to a value in the thermodynamic limit that correlates to the Dicke basis, as proved analytically.

The system under consideration is one of several types of solvable/integrable models described in the literature. Free fermions, 1D interacting models like XXZ and Fermi-Hubbard, and long-range interaction models like Haldane Shastry and Calogero-Sutherland models are all examples. Each of these classes is distinct from the others in terms of both physical characteristics and methods for solving them.

The findings, combined with earlier findings for 1D systems, show that integrable systems have a far from the greatest average entanglement value, which could be used to differentiate them from chaotic systems.

Nonetheless, at the thermodynamic limit, various classes of integrable models can have varied average EE values while still being far off the maximum. This also raises the idea that the average EE’s exact value defines the group of integrable models. 

Journal Reference

Kumari, M. & Alhambra, A. M. (2022) Eigenstate entanglement in integrable collective spin models. Quantum, 6, p. 701. Available Online: https://quantum-journal.org/papers/q-2022-04-27-701/pdf/

References and Further Reading

  1. Arnold, V I (2013) Mathematical methods of classical mechanics'. In: Graduate Texts in Mathematics, 60, Springer Science & Business Media. doi.org/10.1007/978-1-4757-2063-1.
  2. Babelon, O., et al. (2003) Introduction to classical integrable systems'. In: Cambridge Monographs on Mathematical Physics, Cambridge University Press. doi.org/10.1017/CBO9780511535024.
  3. Caux, J-S & Mossel, J (2011) Remarks on the notion of quantum integrability. Journal of Statistical Mechanics: Theory and Experiment, 2011, p. P02023. doi.org/10.1088/1742-5468/2011/02/p02023.
  4. Baxter, R J (1985) Exactly solved models in statistical mechanics. Integrable Systems in Statistical Mechanics, pp. 5–63. doi.org/10.1142/9789814415255_0002.
  5. Gaudin, M (2014) The be the wavefunction. In: Physics and Astronomy, Theoretical Physics and Mathematical Physics, Statistical Physics, Cambridge University Press. doi.org/10.1017/CBO9781107053885.
  6. Bethe, H (1931) Zur theorie der metalle'. Zeitschrift für Physik, 71, pp. 205–226. doi.org/10.1007/BF01341708.
  7. Berry, M V & Tabor, M (1977) Level clustering in the regular spectrum. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 356(1686), pp. 375–394. doi.org/10.1098/rspa.1977.0140.
  8. Lewis-Swan, R. J., et al. (2019) Dynamics of quantum information. Nature Reviews Physics, 1, pp. 627–634. doi.org/10.1038/s42254-019-0090-y.
  9. Chiara, G. D., et al. (2006) Entanglement entropy dynamics of heisenberg chains. Journal of Statistical Mechanics: Theory and Experiment, 2006, p. P03001. doi.org/10.1088/1742-5468/2006/03/p03001.
  10. Cincio, L., et al. (2007) Entropy of entanglement and correlations induced by a quench: Dynamics of a quantum phase transition in the quantum ising model. Physical Review A, 75(5), p. 052321. doi.org/10.1103/PhysRevA.75.052321.
  11. Fagotti, M & Calabrese, P (2008) Evolution of entanglement entropy following a quantum quench: Analytic results for the xyxy chain in a transverse magnetic field. Physical Review A, 78(1), p. 010306. doi.org/10.1103/PhysRevA.78.010306.
  12. Kim, H & Huse, D A (2013) Ballistic spreading of entanglement in a diffusive nonintegrable system. Physical Review Letters, 111(12), p. 127205. doi.org/10.1103/PhysRevLett.111.127205.
  13. Olalla A., et al. (2020) Entanglement oscillations near a quantum critical point. Physical Review Letters, 124(23), p. 230601. doi.org/10.1103/PhysRevLett.124.230601.
  14. Bardarson, J. H., et al. (2012) Unbounded growth of entanglement in models of many-body localization. Physical Review Letters, 109(1), p. 017202. doi.org/10.1103/PhysRevLett.109.017202.
  15. Serbyn, M., et al. (2013) Universal slow growth of entanglement in interacting strongly disordered systems. Physical Review Letters, 110(26), p. 260601. doi.org/10.1103/PhysRevLett.110.260601.
  16. Friesdorf, M., et al. (2015) Many-body localization implies that eigenvectors are matrix-product states. Physical Review Letters, 114(17), p. 170505. doi.org/10.1103/PhysRevLett.114.170505.
  17. Turner, C. J., et al. (2018) Quantum scarred eigenstates in a rydberg atom chain: Entanglement, breakdown of thermalization, and stability to perturbations. Physical Review B, 98(15), p. 155134. doi.org/10.1103/PhysRevB.98.155134.
  18. Ho, W. W., et al. (2019) Periodic orbits, entanglement, and quantum many-body scars in constrained models: Matrix product state approach. Physical Review Letters, 122(4), p. 040603. doi.org/10.1103/PhysRevLett.122.040603.
  19. Lewis-Swan, R. J., et al. (2019) Unifying scrambling, thermalization and entanglement through measurement of fidelity out-of-time-order correlators in the dicke model. Nature Communications, 10, p. 1581. doi.org/10.1038/s41467-019-09436-y.
  20. Chaudhury, S., et al. (2009) Quantum signatures of chaos in a kicked top. Nature, 461, pp. 768–771. doi.org/10.1038/nature08396.
  21. Neill, C., et al. (2016) Ergodic dynamics and thermalization in an isolated quantum system. Nature Physics, 12, pp. 1037–1041. doi.org/10.1038/nphys3830.
  22. Nielsen, M A & Chuang, I L (2010) Quantum computation and quantum information: 10th anniversary edition. In: Cambridge University Press. doi.org/10.1017/CBO9780511976667.
  23. Beugeling, W., et al. (2015) Global characteristics of all eigenstates of local many-body hamiltonians: participation ratio and entanglement entropy. Journal of Statistical Mechanics: Theory and Experiment, 2015, p. P02002. doi.org/10.1088/1742-5468/2015/02/p02002.
  24. Vidmar, L & Rigol, M (2017) Entanglement entropy of eigenstates of quantum chaotic hamiltonians. Physical Review Letters, 119(22), p. 220603. doi.org/10.1103/PhysRevLett.119.220603.
  25. Murthy, C & Srednicki, M (2019) Structure of chaotic eigenstates and their entanglement entropy. Physical Review E, 100(2), p. 022131. doi.org/10.1103/PhysRevE.100.022131.
  26. Huang, Y (2019) Universal eigenstate entanglement of chaotic local hamiltonians. Nuclear Physics B, 938, pp. 594–604. doi.org/10.1016/j.nuclphysb.2018.09.013.
  27. Page, D N (1993) Average entropy of a subsystem. Physical Review Letters, 71(9), pp. 1291–1294. doi.org/10.1103/PhysRevLett.71.1291.
  28. Vidmar, L., et al. (2017) Entanglement entropy of eigenstates of quadratic fermionic hamiltonians. Physical Review Letters, 119(2), p. 020601. doi.org/10.1103/PhysRevLett.119.020601.
  29. Hackl, L., et al. (2019) Average eigenstate entanglement entropy of the xy chain in a transverse field and its universality for translationally invariant quadratic fermionic models. Physical Review B, 99(7), p. 075123. doi.org/10.1103/PhysRevB.99.075123.
  30. Łydżba, P., et al. (2020) Eigenstate entanglement entropy in random quadratic hamiltonians. Physical Review Letters, 125(18), p. 180604. doi.org/10.1103/PhysRevLett.125.180604.
  31. LeBlond, T., et al. (2019) Entanglement and matrix elements of observables in interacting integrable systems. Physical Review E, 100(6), p. 062134. doi.org/10.1103/PhysRevE.100.062134.
  32. Keating, J. P., et al. (2015) Spectra and eigenstates of spin chain hamiltonians. Communications in Mathematical Physics, 338, pp. 81–102. doi.org/10.1007/s00220-015-2366-0.
  33. Bauer, B & Nayak, C (2013) Area laws in a many-body localized state and its implications for topological order. Journal of Statistical Mechanics: Theory and Experiment, 2013, p. P09005. doi.org/10.1088/1742-5468/2013/09/p09005.
  34. Lombardi, M & Matzkin, A (2011) Entanglement and chaos in the kicked top. Physical Review E, 83(1), p. 016207. doi.org/10.1103/PhysRevE.83.016207.
  35. Madhok, V (2015) Comment on “entanglement and chaos in the kicked top”. Physical Review E, 92(3), p. 036901. doi.org/10.1103/PhysRevE.92.036901.
  36. Lombardi, M & Matzkin, A (2015) Reply to “comment on ‘entanglement and chaos in the kicked top’”. Physical Review E, 92(3), p. 036902. doi.org/10.1103/PhysRevE.92.036902.
  37. Ruebeck, J. B., et al. (2017) Entanglement and its relationship to classical dynamics. Physical Review E, 95(6), p. 062222. doi.org/10.1103/PhysRevE.95.062222.
  38. Kumari, M & Ghose, S (2019) Untangling entanglement and chaos. Physical Review A, 99(4), p. 042311. doi.org/10.1103/PhysRevA.99.042311.
  39. Dogra, S., et al. (2017) Quantum signatures of chaos, thermalization, and tunneling in the exactly solvable few-body kicked top. Physical Review E, 99(6), p. 062217. doi.org/10.1103/PhysRevE.99.062217.
  40. Harrow, A W (2013) The church of the symmetric subspace. In: Quantum Physics (quant-ph), arXiv:1308.6595. doi.org/10.48550/arXiv.1308.6595.
  41. Stockton, J. K., et al. (2003) Characterizing the entanglement of symmetric many-particle spin-1212 systems. Physical Review A, 67(2), p. 022112. doi.org/10.1103/PhysRevA.67.022112.
  42. Lipkin, H. J., et al. (1965) Validity of many-body approximation methods for a solvable model: (i). exact solutions and perturbation theory. Nuclear Physics, 62(2), pp. 188–198. doi.org/10.1016/0029-5582(65)90862-X.
  43. Meshkov, N., et al. (1965) Validity of many-body approximation methods for a solvable model: (ii). linearization procedures. Nuclear Physics, 62(2), pp. 199–210. doi.org/10.1016/0029-5582(65)90863-1.
  44. Glick, A. J., et al. (1965) Validity of many-body approximation methods for a solvable model: (iii). diagram summations. Nuclear Physics, 62(2), pp. 211–224. doi.org/10.1016/0029-5582(65)90864-3.
  45. Castaños, O., et al. (2006) Classical and quantum phase transitions in the lipkin-meshkov-glick model. Physical Review B, 74(10), p. 104118. doi.org/10.1103/PhysRevB.74.104118.
  46. Vidal, J., et al. (2007) Entanglement entropy in collective models. Journal of Statistical Mechanics: Theory and Experiment, 2007, p. P01015. doi.org/10.1088/1742-5468/2007/01/p01015.
  47. Arias, M. H. M., et al. (2021) Nonlinear dynamics and quantum chaos of a family of kicked pp-spin models. Physical Review E, 103(5), p. 052212. doi.org/10.1103/PhysRevE.103.052212.
  48. Arias, M. H. M., et al. (2020) Simulation of the complex dynamics of mean-field pp-spin models using measurement-based quantum feedback control. Physical Review A, 102(2), p. 022610. doi.org/10.1103/PhysRevA.102.022610.
  49. Lerma-Hernández, S., et al. (2018) Analytical description of the survival probability of coherent states in regular regimes. Journal of Physics A: Mathematical and Theoretical, 51(47), p. 475302. doi.org/10.1088/1751-8121/aae2c3.
  50. Chinni, K., et al. (2021) Effect of chaos on the simulation of quantum critical phenomena in analog quantum simulators. Physical Review Research, 3(3), p. 033145. doi.org/10.1103/PhysRevResearch.3.033145.
  51. Richardson. R W (1963) A restricted class of exact eigenstates of the pairing-force hamiltonian. Physics Letters, 3(6), pp. 277–279. doi.org/10.1016/0031-9163(63)90259-2.
  52. Richardson, R W & Sherman, N (1964) Exact eigenstates of the pairing-force hamiltonian. Nuclear Physics, 52, pp. 221–238. doi.org/10.1016/0029-5582(64)90687-X.
  53. Łydżba, P., et al. (2021) Entanglement in many-body eigenstates of quantum-chaotic quadratic hamiltonians. Physical Review B, 103(10), p. 104206. doi.org/10.1103/PhysRevB.103.104206.
  54. Ribeiro, P., et al. (2007) Thermodynamical limit of the lipkin-meshkov-glick model. Physical Review Letters, 99(5), p. 050402. doi.org/10.1103/PhysRevLett.99.050402.
  55. Ribeiro, P., et al. (2008) Exact spectrum of the lipkin-meshkov-glick model in the thermodynamic limit and finite-size corrections. Physical Review E, 78(2), p. 021106. doi.org/10.1103/PhysRevE.78.021106.
  56. Dicke, R H (1954) Coherence in spontaneous radiation processes. Physical Review Journals Archive, 93(1), pp. 99–110. doi.org/10.1103/PhysRev.93.99.
  57. Moreno, M G M & Parisio, F (2018) All bipartitions of arbitrary dicke states. In: Quantum Physics (quant-ph). doi.org/10.48550/arXiv.1801.00762.
  58. Latorre, J. I., et al. (2005) Entanglement entropy in the lipkin-meshkov-glick model. Physical Review A, 71(6), p. 064101. doi.org/10.1103/PhysRevA.71.064101.
  59. Cichoń, J., et al. (2013) On delta-method of moments and probabilistic sums. In: 2013 Proceedings of the Tenth Workshop on Analytic Algorithmics and Combinatorics (ANALCO), SIAM, pp. 91–98. doi.org/10.1137/1.9781611973037.11.
  60. Santos, L. F., et al. (2016) Excited-state quantum phase transitions in many-body systems with infinite-range interaction: Localization, dynamics, and bifurcation. Physical Review A, 94(1), p. 012113. doi.org/10.1103/PhysRevA.94.012113.
  61. Pappalardi, S., et al. (2018) Scrambling and entanglement spreading in long-range spin chains. Physical Review B, 98(13), p. 134303. doi.org/10.1103/PhysRevB.98.134303.
  62. Cejnar, P., et al. (2021) Excited-state quantum phase transitions. Journal of Physics A: Mathematical and Theoretical, 54(13), p. 133001. doi.org/10.1088/1751-8121/abdfe8.
  63. Nader, D. J., et al. (2021) Avoided crossings and dynamical tunneling close to excited-state quantum phase transitions. Physical Review E, 104(6), p. 064116. doi.org/10.1103/PhysRevE.104.064116.
  64. Seshadri, A., et al. (2018) Tripartite mutual information, entanglement, and scrambling in permutation symmetric systems with an application to quantum chaos. Physical Review E, 98(5), p. 052205. doi.org/10.1103/PhysRevE.98.052205.
  65. Kumari, M & Alhambra, A M (2022) Eigenstate entanglement in nonintegrable collective spin models. In preparation.
  66. Pilatowsky-Cameo, S., et al. (2020) Positive quantum lyapunov exponents in experimental systems with a regular classical limit. Physical Review E, 101(1), p. 010202. doi.org/10.1103/PhysRevE.101.010202.
  67. Vidal, G., et al. (2003) Entanglement in quantum critical phenomena. Physical Review Letters, 90(22), p. 227902. doi.org/10.1103/PhysRevLett.90.227902.
  68. He, P., et al. (2019) Engineering spin squeezing in a 3d optical lattice with interacting spin-orbit-coupled fermions. Physical Review Research, 1(3), p. 033075. doi.org/10.1103/PhysRevResearch.1.033075.
  69. Muñoz Arias, M. H., et al. (2020) Simulating nonlinear dynamics of collective spins via quantum measurement and feedback. Physical Review Letters, 124(11), p. 110503. doi.org/10.1103/PhysRevLett.124.110503.
  70. Sieberer, L. M., et al. (2019) Digital quantum simulation, trotter errors, and quantum chaos of the kicked top. npj | Quantum Information, 5, p. 78. doi.org/10.1038/s41534-019-0192-5.
  71. Martin, M. J., et al. (2013) A quantum many-body spin system in an optical lattice clock. Science, 341(6146), pp. 632–636. doi.org/10.1126/science.1236929.
  72. Wang, X & Mølmer, K (2002) Pairwise entanglement in symmetric multi-qubit systems. The European Physical Journal D - Atomic, Molecular, Optical and Plasma Physics, 18, pp. 385–391. doi.org/10.1140/epjd/e20020045.
  73. Kumari, M., et al. (2017) Sufficient condition for nonexistence of symmetric extension of qudits using bell inequalities. Physical Review A, 96(1), p. 012128. doi.org/10.1103/PhysRevA.96.012128.

Tell Us What You Think

Do you have a review, update or anything you would like to add to this article?

Leave your feedback
(Logout)
Your comment type
Submit

Newsletters you may be interested in

See all Newsletters »

Terms

While we only use edited and approved content for Azthena answers, it may on occasions provide incorrect responses. Please confirm any data provided with the related suppliers or authors. We do not provide medical advice, if you search for medical information you must always consult a medical professional before acting on any information provided.

Your questions, but not your email details will be shared with OpenAI and retained for 30 days in accordance with their privacy principles.

Please do not ask questions that use sensitive or confidential information.

Read the full Terms & Conditions.

Provide Feedback