Proposing a Definition for Quantum Superpositions of Causal Orders

By Skyla BailyMar 8 2022

Quantum superpositions can be thought of as broadenings of classical probabilities: if there are uncertainties between two alternatives, each with a probability, it should be possible to consider a superposition of the two, with complex amplitudes replacing probabilities. This intuition is famously leveraged by Feynman’s sum-over-histories approach. This study explores new research in the journal Quantum.

Study: A no-go theorem for superpositions of causal orders. Image Credit: CI Photos/Shutterstock.com

To what extent can the superposition principle be generalized beyond its original scope of application? Quantum superpositions, unlike classical probabilities, have no clear interpretation, and hence providing a general, principled answer to this question is difficult.

Combining the principles of quantum theory and general relativity is one of the main motivations. Despite recent research, the scenarios examined so far do not support a direct interpretation as causal order superpositions. The so-called “quantum switch” (Figure 1), in which a control system defines the order in which a set of operations acts on a target, is the most widely discussed example.

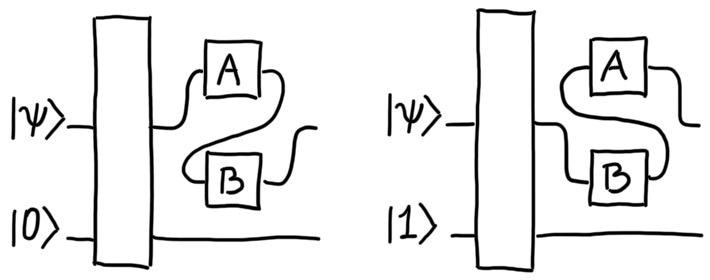
Figure 1. The quantum switch. The state of a control system determines the order of two operations on a target system. Image Credit: Costa, 2022

The quantum switch, which is commonly referred to as a “superposition of causal orders,” is better understood as “entanglement” between causal relations and the control system. The quantum switch is unrecognizable from a probabilistic mixture of causal orders if the control is removed. Is it possible to have a “pure”, deterministic superposition of causal orders (Figure 2) without any additional control system?

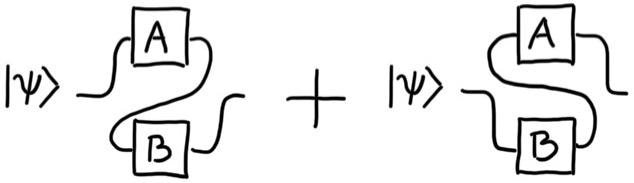
Figure 2. Pure superposition of causal orders. Is it possible to superpose the causal order of two events, without the aid of a control system? Image Credit: Costa, 2022

The current study proposes a definition of causal order superpositions and finds a negative result, ruling out the most obvious candidates. The researchers show that superpositions of two different causal orders are not possible for unitary Markovian processes where all systems have equal dimensions, in the context that they do not comprise valid, deterministic processes.

Discussion

It is natural to define the superposition of two unitaries as a linear combination for some complex numbers interpreted as probability amplitudes when given two unitaries. However, a “superposition” is not always a unitary operator.

The issue with this interpretation is that the postselection step necessitates obtaining one of a set of possible measurement outcomes. As a result, this research is only interested in processes that can be implemented without the use of postselection. Superposition is not a universal possibility for processes, as it is for states. There are some unitaries, however, for which superpositions are possible.

For processes involving more than two events, superpositions of causal orders become significant. An “event” is a specific operation that occurs at a specific time, while a “process” is a collection of unitaries that connects the events. The researchers are only interested in processes that can be implemented without the use of post-processing. As a result, the processes were assumed to be deterministic.

The causal nonseparability of a superposition of differently ordered processes is unavoidable. The existence of locally classical, causally nonseparable processes, on the other hand, indicates that the converse is not true, rendering causal nonseparability unsuitable for describing superpositions of causal orders.

As a generalization of density matrices, process matrices cannot be directly superposed. A linear combination is used to define the superposition of two pure processes. The process matrix reduces to a state when all parties only have input and the superposition of processes diminishes to the superposition of states.

A pure process, in general, defines an isometry from all output to all input spaces. The process defines a unitary transformation from outputs to inputs in the case where the total input and output dimensions are equal. The term unitary process indicates such processes.

Two different versions of the quantum switch are relevant to the current discussion. The first is a three-part process, and the second includes an additional laboratory where both the control and target systems can be prepared. The unitary process that results is the sum of two vectors, each of which is responsible for a different causal order.

Although it is unknown whether a superposition of causal orders is possible in general, it can be ruled out in the case of Markovian processes in general. A sequence of unitaries constitutes a unitary Markovian process.

As a result, a linear combination of two unitary, Markovian processes with various orders cannot fulfill the process vector normalization constraints in the simplest fourpartite case. The simplest, most intuitive superpositions of causal orders are ruled out by this result. It proves, in particular, that the control system is required for the quantum switch to be valid.

Conclusion

When the order of events is not correlated with any other system, superpositions of processes with different causal orders are strongly constrained. Superposing sequences of equal-dimension unitaries linking events in different orders is not possible. It is currently unknown whether it is plausible to superpose unitary, differently ordered processes that do not satisfy Markovianity or do not have equal dimensions in the local input and output spaces.

Furthermore, developing a notion of “coherence” of causal orders that applies to nonpure processes, possibly generalizing corresponding resource theories for states, is an intriguing possibility.

Journal Reference:

Costa, F. (2022) A no-go theorem for superpositions of causal orders. Quantum, 6, p. 663. Available Online: https://quantum-journal.org/papers/q-2022-03-01-663/

References and Further Reading

1. Feynman, R P (1948) Space-Time Approach to Non-Relativistic Quantum Mechanics. Reviews of Modern Physics, 20, pp. 367–387. doi.org/10.1103/RevModPhys.20.367.
2. Butterfield and C. Isham, Spacetime and the philosophical challenge of quantum gravity, pp. 33–89. Cambridge University Press. doi.org/10.1017/CBO9780511612909.003.
3. Hardy, L (2007) Towards quantum gravity: a framework for probabilistic theories with non-fixed causal structure. Journal of Physics A Mathematical and General, 40, pp. 3081–3099. doi.org/10.1088/1751-8113/40/12/S12.
4. Zych, M., et al. (2019) Bell’s theorem for temporal order Nature Communications,10, p. s3772. doi.org/10.1038/s41467-019-11579-x.
5. Procopio, L. M., et al. (2015) Experimental superposition of orders of quantum gates. Nature Communications, 6, p. 7913. doi.org/10.1038/ncomms8913.
6. Rubino, G., et al. (2017) Experimental verification of an indefinite causal order, Science Advances, 3, p. e1602589. doi.org/10.1126/sciadv.1602589.
7. Rubino, G., et al. (2022) Experimental entanglement of temporal order. Quantum, 6, p. 621. doi.org/10.22331/q-2022-01-11-621.
8. Goswami, K., et al. (2018) Indefinite Causal Order in a Quantum Switch. Physical Review Letters, 121, p. 090503. doi.org/10.1103/PhysRevLett.121.090503.
9. Goswami, K., et al. (2020) Increasing communication capacity via superposition of order. Physical Review Research, 2, p. 033292. doi.org/10.1103/PhysRevResearch.2.033292.
10. Guo, Y., et al. (2020) Experimental Transmission of Quantum Information Using a Superposition of Causal Orders. Physical Review Letters, 124, p. 030502. doi.org/10.1103/PhysRevLett.124.030502.
11. Wei, K., et al. (2019) Experimental Quantum Switching for Exponentially Superior Quantum Communication Complexity. Physical Review Letters, 122, p. 120504. doi.org/10.1103/PhysRevLett.122.120504.
12. Taddei, M. M., et al. (2021) Computational Advantage from the Quantum Superposition of Multiple Temporal Orders of Photonic Gates. PRX Quantum, 2, p. 010320. doi.org/10.1103/PRXQuantum.2.010320.
13. Chiribella, G., et al. (2013) Quantum computations without definite causal structure. Physical Review A, 88, p. 022318. doi.org/10.1103/PhysRevA.88.022318.
14. Chiribella, G (2012) Perfect discrimination of no-signalling channels via quantum superposition of causal structures. Physical Review A, 86, p. 040301(R). doi.org/10.1103/PhysRevA.86.040301.
15. Colnaghi, T., et al. (2012) Quantum computation with programmable connections between gates. Physical Review A, 376, pp. 2940–2943. doi.org/10.1016/j.physleta.2012.08.028.
16. Araújo, M., et al. (2014) Computational Advantage from Quantum-Controlled Ordering of Gates. Physical Review Letters, 113, p. 250402. doi.org/10.1103/PhysRevLett.113.250402.
17. Feix, A., et al. (2015) Quantum superposition of the order of parties as a communication resource. Physical ReviewA, 92, p. 052326. doi.org/10.1103/PhysRevA.92.052326.
18. Guérin, P. A., et al. (2016) Exponential Communication Complexity Advantage from Quantum Superposition of the Direction of Communication. Physical Review Letters, 117, p. 100502. doi.org/10.1103/PhysRevLett.117.100502.
19. Ebler, D., et al. (2018) Enhanced Communication with the Assistance of Indefinite Causal Order. Physical Review Letters, 120, p. 120502. doi.org/10.1103/physrevlett.120.120502.
20. Salek,S., et al. Quantum communication in a superposition of causal orders. doi.org/10.48550/arXiv.1809.06655.
21. Gupta, M K & Sen, UTransmitting quantum information by superposing causal order of mutually unbiased measurements. doi.org/10.48550/arXiv.1909.13125.
22. Aharonov, Y., et al. (1990) Superpositions of time evolutions of a quantum system and a quantum time-translation machine. Physical Review Letters, 64, p. 2965. doi.org/10.1103/PhysRevLett.64.2965.
23. Oreshkov, O., et al. (2012) Quantum correlations with no causal order. Nature Communications, 3, p. 1092. doi.org/10.1038/ncomms2076.
24. Oeckl, R (2003) A “general boundary” formulation for quantum mechanics and quantum gravity. Physics Letters B,575, pp. 318–324. doi.org/10.1016/j.physletb.2003.08.043.
25. Aharonov, Y., et al. (2009) Multiple-time states and multiple-time measurements in quantum mechanics. Physics Letters A, 79, p. 052110. doi.org/10.1103/PhysRevA.79.052110.
26. Cotler, J., et al. (2018) Superdensity operators for spacetime quantum mechanics. Journal of High Energy Physics, p. 93. doi.org/10.1007/jhep09(2018)093.
27. Silva, R., et al. (2017) Connecting processes with indefinite causal order and multi-time quantum states. New Journal of Physics, 19, p. 103022. doi.org/10.1088/1367-2630/aa84fe.
28. Barrett, J., et al. Quantum Causal Models.doi.org/10.48550/arXiv.1906.10726.
29. Guérin, P A & Brukner, Č (2018) Observer-dependent locality of quantum events. New Journal of Physics, 20, p. 103031. doi.org/10.1088/1367-2630/aae742.
30. Oreshkov, O (2019) Time-delocalized quantum subsystems and operations: on the existence of processes with indefinite causal structure in quantum mechanics. Quantum, 3, p. 206. doi.org/10.22331/q-2019-12-02-206.
31. Heinosaari, T & Ziman, M (2011) The Mathematical Language of Quantum Theory: From Uncertainty to Entanglement. Cambridge University Press, doi.org/10.1017/CBO9781139031103.
32. Choi, M D (1975) Completely positive linear maps on complex matrices,'' Linear Algebra and Its Applications, 10, pp. 285–290. doi.org/10.1016/0024-3795(75)90075-0.
33. Jamiołkowski, A (1972) Linear transformations which preserve trace and positive semidefiniteness of operators. Reports on Mathematical Physics,3, pp. 275–278. doi.org/10.1016/0034-4877(72)90011-0.
34. Shrapnel, S., et al. (2018) Updating the Born rule. New Journal of Physics,20, p. 053010. doi.org/10.1088/1367-2630/aabe12.
35. Oreshkov, O & Cerf, N J (2016) Operational quantum theory without predefined time. New Journal of Physics, 18, p. 073037. doi.org/10.1088/1367-2630/18/7/073037.
36. Milz, S., et al. (2018) Entanglement, non-Markovianity, and causal non-separability. New Journal of Physics, 20, p. 033033. doi.org/10.1088/1367-2630/aaafee.
37. Oreshkov, O & Giarmatzi, C (2016) Causal and causally separable processes.New Journal of Physics, 18, p. 093020. doi.org/10.1088/1367-2630/18/9/093020.
38. Wechs, J., et al. (2019) On the definition and characterisation of multipartite causal (non)separability. New Journal of Physics, 21, p. 013027. doi.org/10.1088/1367-2630/aaf352.
39. Baumeler, Ä., et al. (2014) Maximal incompatibility of locally classical behavior and global causal order in multi-party scenarios. Physical Review A, 90, p. 042106. doi.org/10.1103/PhysRevA.90.042106.
40. Baumeler, Ä & Wolf, S (2016) The space of logically consistent classical processes without causal order. New Journal of Physics, 18, p. 013036.doi.org/10.1088/1367-2630/18/1/013036.
41. Baumeler, Ä., et al. (2019) Reversible time travel with freedom of choice. Classical and Quantum Gravity, 36, p. 224002. doi.org/10.1088/1361-6382/ab4973.
42. Tobar, G &Costa, F (2020) Reversible dynamics with closed time-like curves and freedom of choice. Classical and Quantum Gravity, 37, p. 205011.doi.org/10.1088/1361-6382/aba4bc.
43. Araújo, M., et al. (2015) Witnessing causal nonseparability, New Journal of Physics, 17, p. 102001.doi.org/10.1088/1367-2630/17/10/102001.
44. Araújo, M., et al. (2017) A purification postulate for quantum mechanics with indefinite causal order. Quantum, 1, p. 10. doi.org/10.22331/q-2017-04-26-10.
45. Costa, F & Shrapnel, S (2016) Quantum causal modelling. New Journal of Physics, 18, p. 063032. doi.org/10.1088/1367-2630/18/6/063032.
46. Pollock, F. A., et al. (2018) Operational Markov Condition for Quantum Processes. Physical Review Letters, 120, p. 040405. doi.org/10.1103/physrevlett.120.040405.
47. Giarmatzi, C & Costa, F (2021) Witnessing quantum memory in non-Markovian processes. Quantum, 5, p. 440. doi.org/10.22331/q-2021-04-26-440.
48. Yokojima, W., et al. (2021) Consequences of preserving reversibility in quantum superchannels. Quantum, 5, p. 441. doi.org/10.22331/q-2021-04-26-441.
49. Costa, F (2017) A no-go theorem for superpositions of causal order. Space-time and Information, Manitoulin Island, Ontario, Canada. https://uwaterloo.ca/spacetime-information-workshop/abstracts.
50. Theurer, T., et al. (2017) Resource Theory of Superposition. Physical Review Letters, 119, p. 230401. doi.org/10.1103/PhysRevLett.119.230401.
51. Bischof, F., et al. (2019) Resource Theory of Coherence Based on Positive-Operator-Valued Measures. Physical Review Letters, 123, p. 110402. doi.org/10.1103/PhysRevLett.123.110402.