The Casimir effect is a macroscopic quantum phenomenon caused by electromagnetic field quantum fluctuations in a vacuum. Lifshitz created a generalized theory of the phenomena that may be applied to any dielectric body, including metals. The optical characteristics of objects and superconductivity of superconductors have a big impact on the Casimir force, which has been explored in the journal Quantum Reports.

Study: Casimir Effect between Superconducting Plates in the Mixed State. Image Credit: SeniMelihat/Shutterstock.com
The Casimir force is based on changes in Casimir energy caused by changes in superconductor optical characteristics. Recent advances in Casimir force measurements have shown that the Casimir force exists and obeys Lifshitz’s theory. Both transitions generated by temperature changes and transitions caused by an external magnetic field were examined in these studies.
The use of a nanophotonic sensing device on a chip to measure changes in the Casimir force between superconductive plates was presented as an experimental platform. As the external magnetic field rises, the conductivity of type-I superconductors varies suddenly. The magnetic field is initially expelled by the Meissner effect. The superconductivity of type-I superconductors, however, is reduced by a high magnetic field over a critical magnetic field Bc.
The normal phase of the magnetic flux is dictated by the velocity of the vortices. Between the lower critical magnetic field Bc1 and the upper critical magnetic field Bc2, there is a coexisting phase known as the mixed state or magnetic vortex state. In the superconductor, the magnetic flow is quantized.
The magnetic field decays exponentially with London penetration depth in the Meissner condition. The Casimir force between high-Tc superconductors in this condition has been theoretically studied by Villarreal and Caballero-Benitez.
Because the electric characteristics of type-I superconductors, such as aluminum, are well established, they are ideal for validating the Casimir energy transition. Many type-II superconductors, such as high-Tc superconductors, are anisotropic, in contrast. Measuring the Casimir force between superconductors can therefore reveal information on the electrical interplay between vacuum quantum fluctuation and quantum magnetic flux.
In this paper, researchers studied how the applied magnetic field affects the Casimir force between high-Tc superconductors in a mixed state. Because YBCO(YBa2Cu3O7) is a typical type-II superconductor, and the mixed state reflection data were measured, it was chosen as an example. Furthermore, the dissipation in terms of vortex motion helps explain the dependency of the reflectance on the external magnetic field.
The link between the Casimir force and material characteristics of superconductors in the mixed state is summarized in the conclusion section.
Methodology
The angular frequency ω, wave vector k = (k⊥, kz), where k⊥ is defined as the wave vector parallel to the surface, and polarization (transverse magnetic mode (TM) and transverse electric mode (TE) describe the electromagnetic field between the plates, as described in Figure 1.
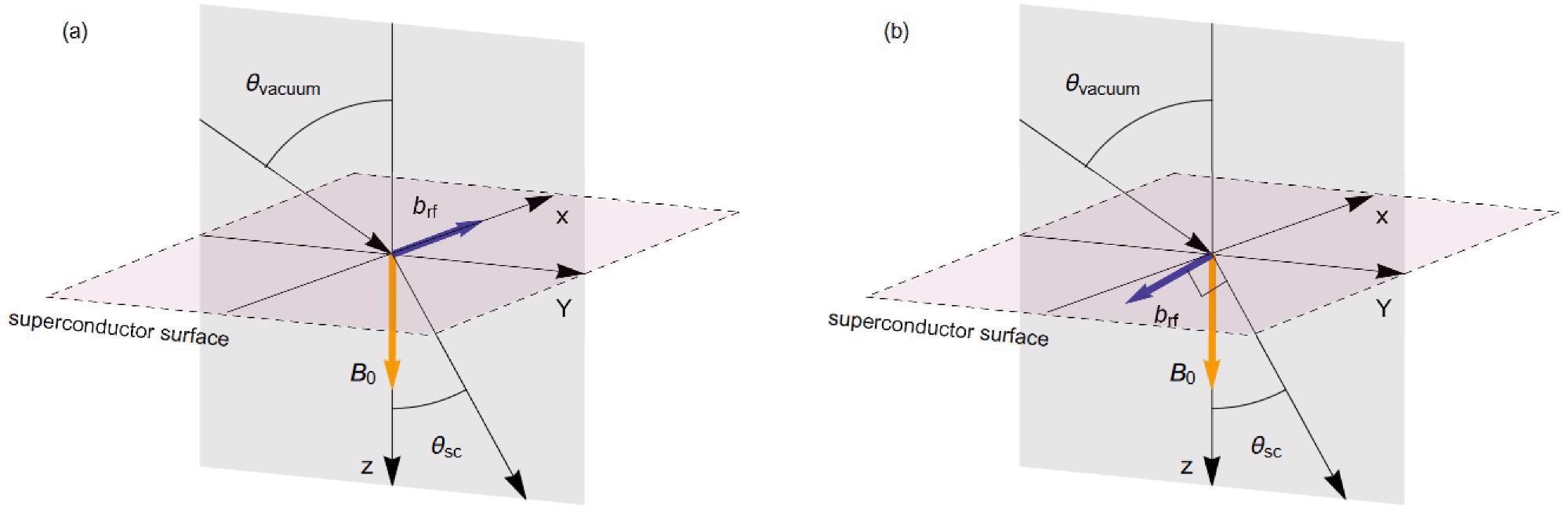
Figure 1. Light propagation in (a) TM mode and (b) TE mode from a vacuum to a superconductor. The yz-plane is the plane of incidence. The external magnetic field B0 is perpendicular to the surface of the superconductor. The magnetic field of the light Blight in TM mode is perpendicular to the plane of incidence. Conversely, the electric field of the light is perpendicular to the plane of incidence, and the magnetic field exits at the yz plane. Image Credit: Inui, 2021
Results
The YBCO’s parameters are presented in Table 1.
Table 1. Parameters for vortex dynamics. Source: Inui, 2021
| . |
. |
| Tc |
88.2 K |
| Tc2 |
87 K |
| λ0 |
140 nm |
| Bc2,0 |
112 T |
| κ0 |
2.1 × 104 N/m2 |
| c0 |
2.0 × 10-7 Ω m |
| c1 |
9.7 × 10-7 Ω m/K |
Figure 2 illustrates the superconductor’s mixed state permittivity along the imaginary axis at t = 0.1 for B = 0 and 10 T.
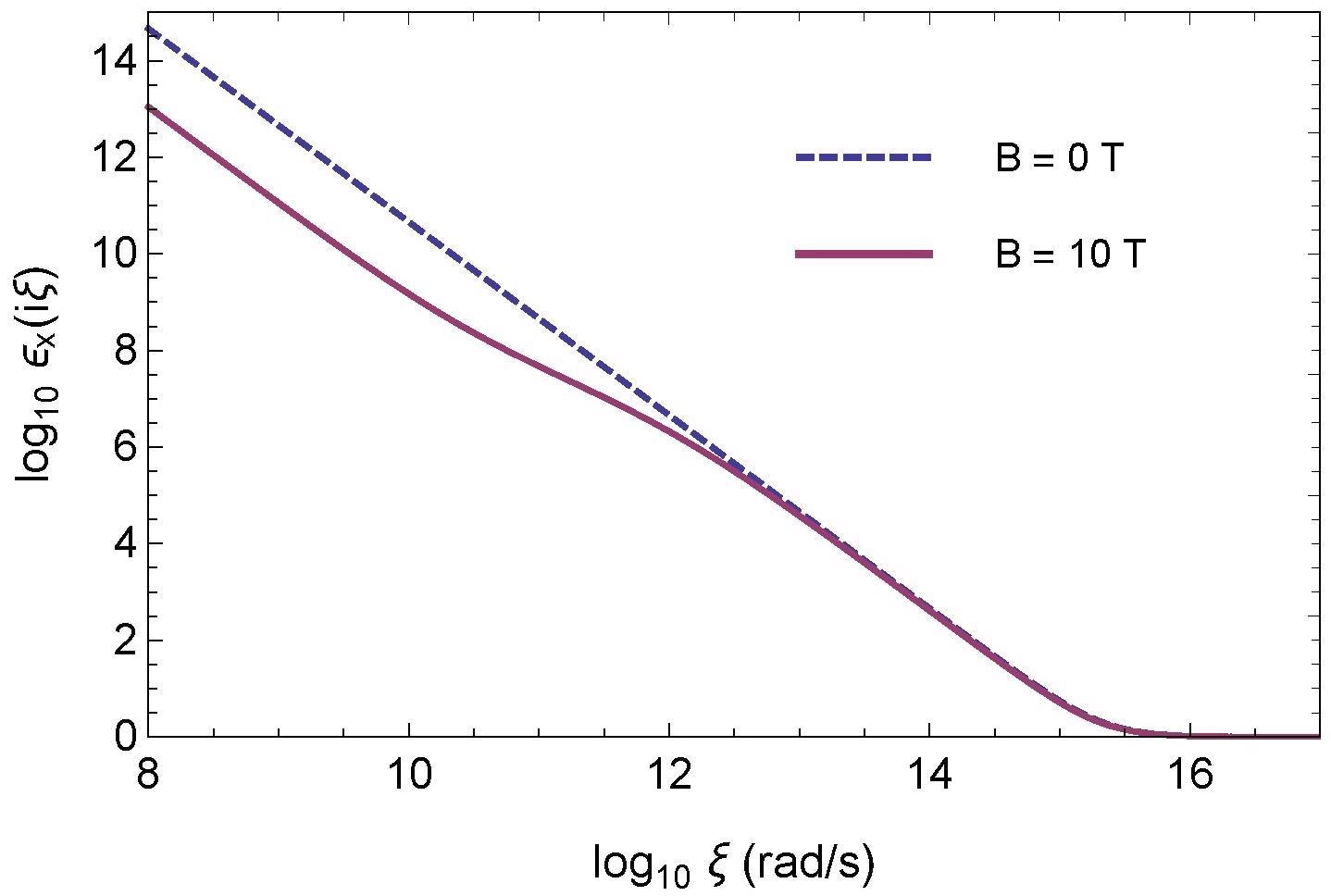
Figure 2. Permittivity parallel to the surface of YBCO in the mixed state at T = 8.82 K (t = 0.1) along imaginary axis in a log–log scale. Image Credit: Inui, 2021
The dependency of plasma frequencies ωp and ωD at t = 0.1 and 0.5, respectively, is shown in Figure 3(a, b).
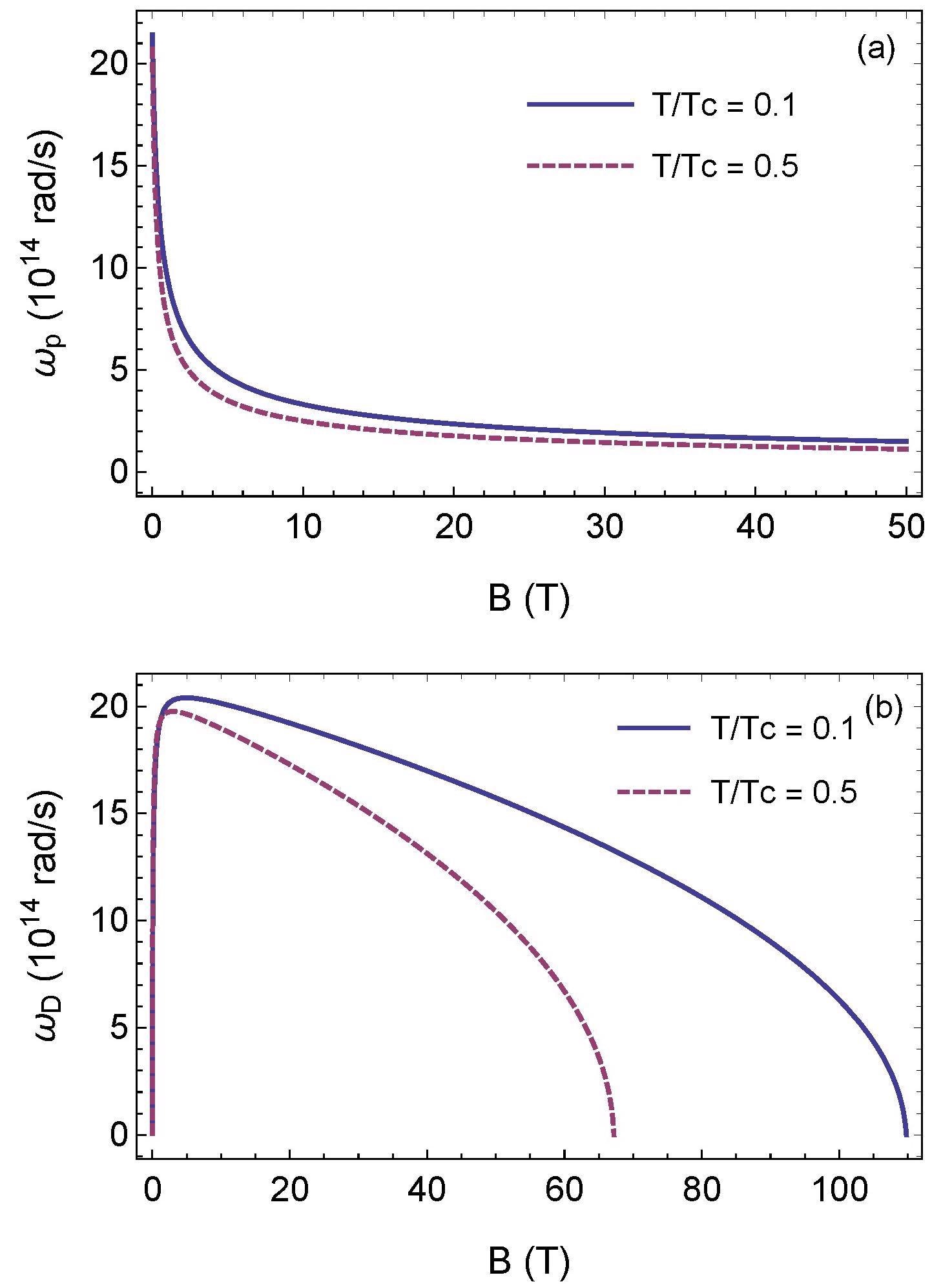
Figure 3. Dependence of frequencies (a) ωp (plasma model) and (b) ωD (Drude model) on magnetic field at t = 0.1 (solid line) and 0.5 (dashed line). Image Credit: Inui, 2021
ωD decreases as the temperature rises, as seen in Figure 4.
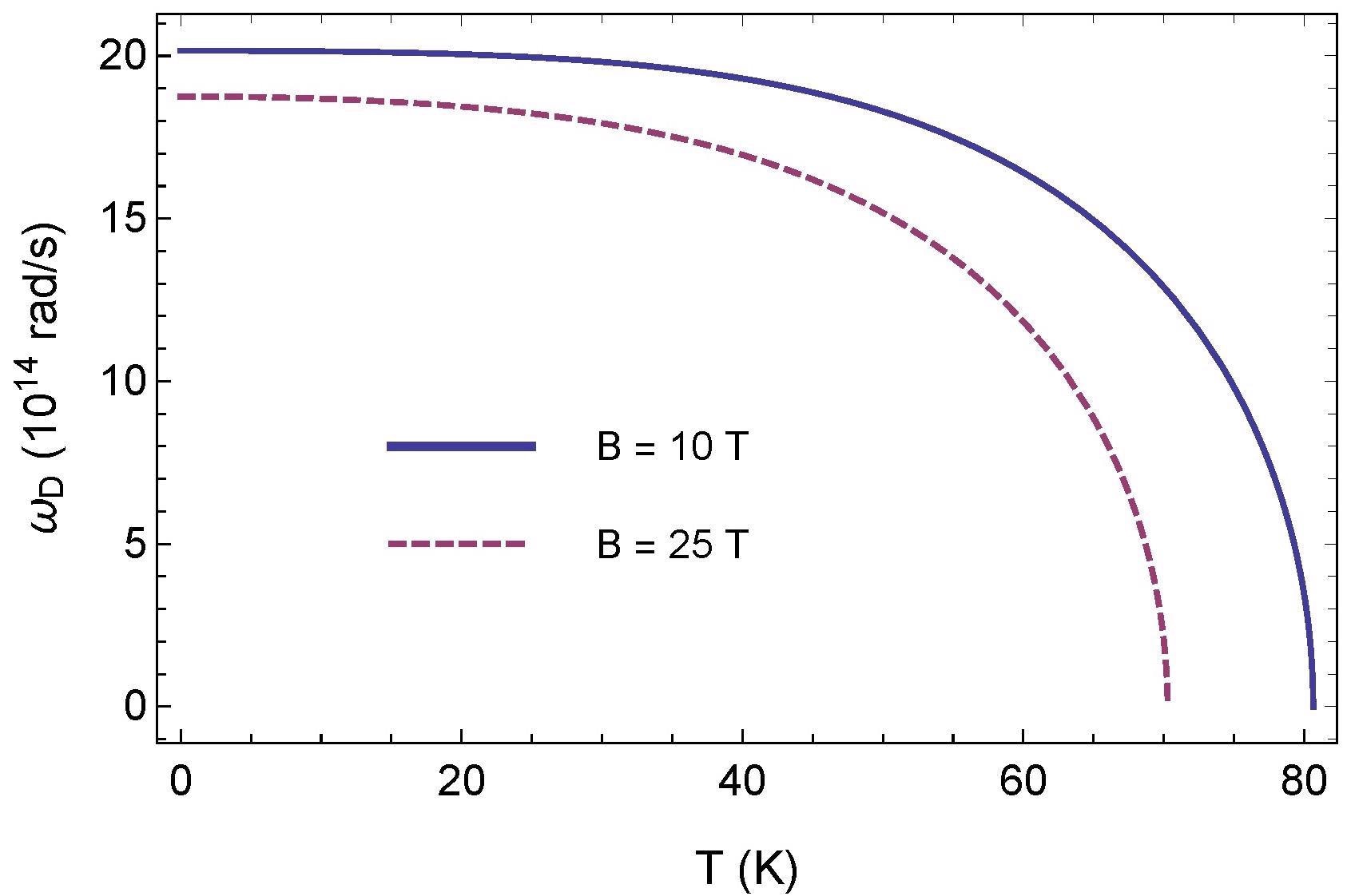
Figure 4. Temperature dependence of frequency ωD (Drude model). Image Credit: Inui, 2021
Figure 5(a) displays the normalized Casimir force ηC = P(a,T)/Pc (a) for a magnetic field between 1 and 60 T at a given separation distance a = 1 μm.
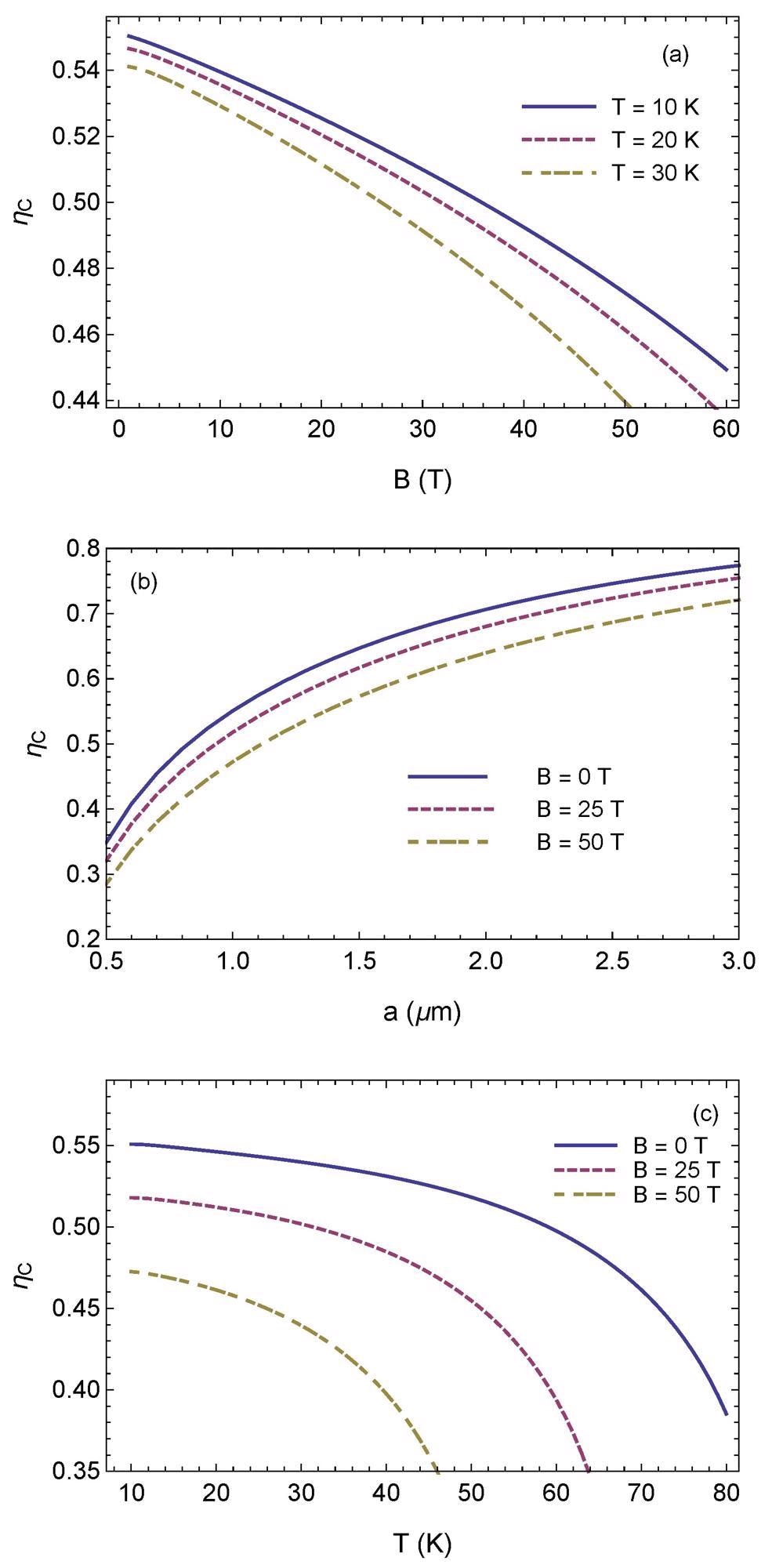
Figure 5. (Color online) Dependence of normalized Casimir force between YBCO plates in the mixed state on (a) magnetic field, (b) separation distance, and (c) temperature. Image Credit: Inui, 2021
Figure 6 shows a comparison of the temperature dependence of the YBCO plate’s Casimir force with and without the Lorentz component.
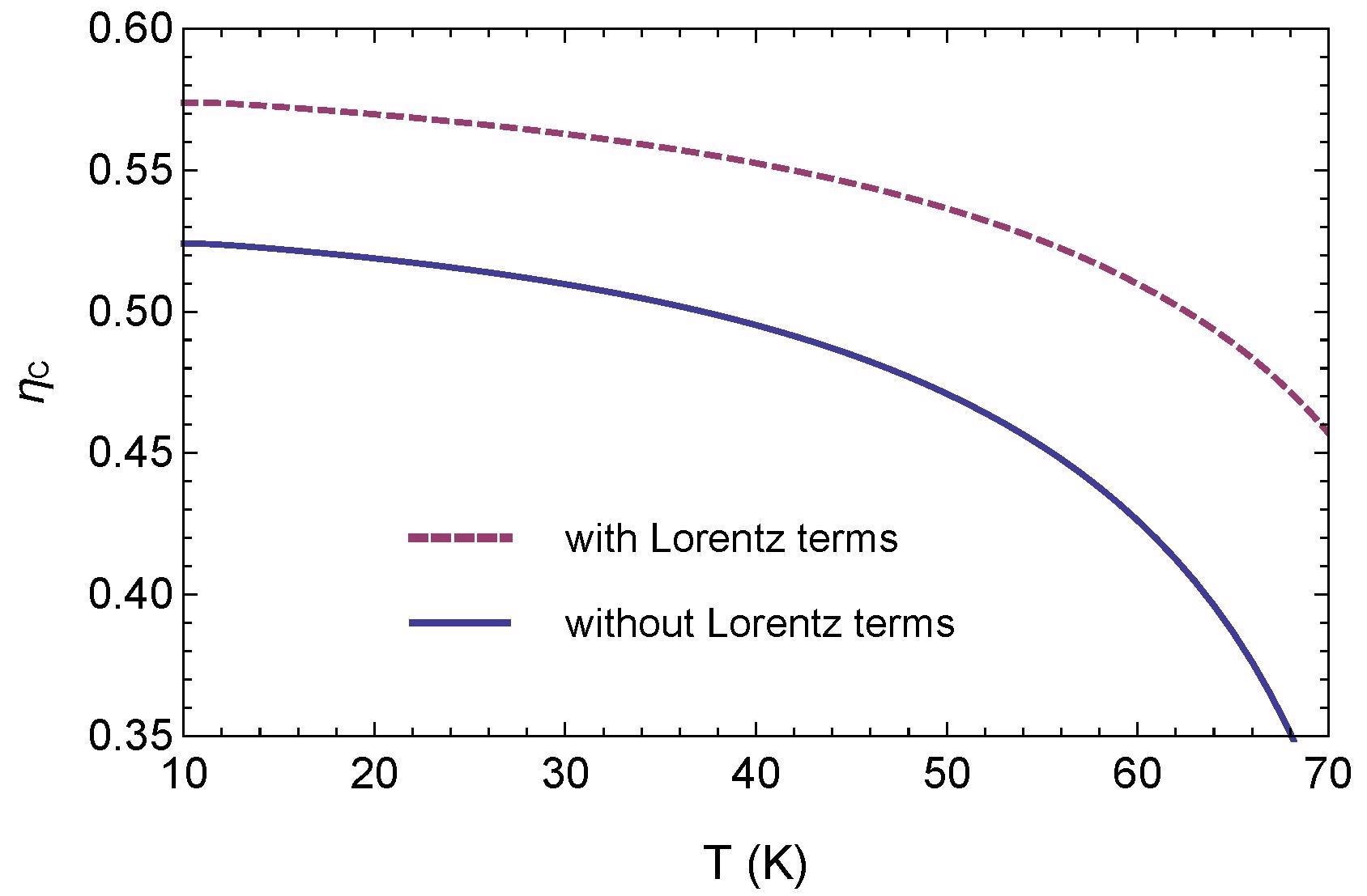
Figure 6. Comparison between normalized Casimir force acting on the superconductive plates with and without terms based on the Lorentz model. Image Credit: Inui, 2021
Conclusion
One of the most essential concepts for determining the superconducting state is the magnetic field penetration depth. The Kramers–Kronig relation was used to determine the permittivity along with the imaginary frequency from the conductivity of superconductors stated in terms of penetration depth. Permittivity was calculated using a set of functions similar to those found in the plasma and Drude models.
The penetration depth was then calculated using the oscillator’s amplitude, and the material dependency of plasma frequencies was calculated using the spring constant. The electrical resistivity in the normal phase was used to calculate the material dependence of the relaxation parameter in the Drude model. A polycrystalline superconductor’s spring constant is stated to be 103 to 104 times lower than that of a single crystal.
The modification of the Casimir force by altering material characteristics has piqued interest. The Casimir force, which is created by irradiating laser pulses over a gold spherical and a Si membrane, is one example. The plasma frequency is related to the charge carrier concentration squared. As a result of the increase in electrons and holes caused by irradiation, the plasma frequency rises and the Casimir force increases.
Optical conductors have not been studied enough for electromagnetic waves with a frequency greater than microwaves in superconductors. As a result, the optical characteristics of the superconductor may be examined by measuring the Casimir force imparted on it (especially for short separation distances), which is dependent on conductivity at higher frequencies.
Journal Reference:
Inui, N (2021) Casimir Effect between Superconducting Plates in the Mixed State. Quantum Reports, 3(4), pp.731-745. Available Online: https://www.mdpi.com/2624-960X/3/4/46/htm
References and Further Reading
- Stange, A., et al. (2021) Science and technology of the Casimir effect. Physics Today, 74, pp. 42–48. doi.org/10.1063/PT.3.4656.
- Lamoreaux, S K (1997) Demonstration of the Casimir force in the 0.6 to 6 μm range. Physical Review Letters, 78, pp. 5–8. doi.org/10.1103/PhysRevLett.78.5.
- Milonni, P W (1994) The Quantum Vacuum; Academic Press: San Diego, CA, USA.
- Bordag, M., et al. (2009) Advances in the Casimir Effect; Oxford University Press: New York, NY, USA.
- Casimir, H B G (1948) On the attraction between two perfectly counducting plates. Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen, 51, pp.793–795.
- Mohideen, U & Roy, A (1998) Precision Measurement of the Casimir Force from 0.1 to 0.9 μm. Physical Review Letters, 81, pp. 4549–4552. doi.org/10.1103/PhysRevLett.81.4549
- Banishev, A. A., et al. (2012) Measurement of the gradient of the Casimir force between a nonmagnetic gold sphere and a magnetic nickel plate. Physical Review B, 85, p. 195422. doi.org/10.1103/PhysRevB.85.195422.
- Banishev, A. A., et al. (2013) Casimir interaction between two magnetic metals in comparison with nonmagnetic test bodies. Physical Review B, 88, p. 155410. doi.org/10.1103/PhysRevB.88.155410.
- Rosa, F. S. S., et al. (2008) Casimir-Lifshitz theory and metamaterials. Physical Review Letters, 100, p. 183602. doi.org/10.1103/PhysRevLett.100.183602.
- Bimonte, G., et al. (2005) Towards measuring variations of Casimir energy by a superconducting cavity. Physical Review Letters, 94, p. 180402. doi.org/10.1103/PhysRevLett.94.180402.
- Bimonte, G., et al. (2005) Variations of Casimir energy from a superconducting transition. Nuclear Physics B, 726, p. 441–463. doi.org/10.1016/j.nuclphysb.2005.08.010.
- Bimonte, G (2008) Casimir effect in a superconducting cavity and the thermal controversy. Physical Review A, 78, p. 062101. doi.org/10.1103/PhysRevA.78.062101.
- Sushkov, A. O., et al. (2011) Observation of the thermal Casimir force. Nature Physics, 7, pp. 230–233. doi.org/10.1038/nphys1909.
- Klimchitskaya, G L & Mostepanenko, V M (2020) Recent measurements of the Casimir force: Comparison between experiment and theory. Modern Physics Letters A, 35, p. 2040007. doi.org/10.1142/S0217732320400076.
- Perez-Morelo, D., et al. (2020) A system for probing Casimir energy corrections to the condensation energy. Microsystems & Nanoengineering, 6, p. 115. doi.org/10.1038/s41378-020-00221-2.
- Norte, R. A., et al. (2018) Platform for Measurements of the Casimir Force between Two Superconductors. Physical Review Letters, 121, p. 030405. doi.org/10.1103/PhysRevLett.121.030405.
- Bimonte, G (2019) Casimir effect between superconductors. Physical Review A, 99, p. 052507. doi.org/10.1103/PhysRevA.99.052507.
- Quach, J Q (2015) Gravitational Casimir Effect. Physical Review Letters, 114, p. 081104. doi.org/10.1103/PhysRevLett.114.081104.
- Golosovsky, M., et al. (1996) High-frequency vortex dynamics in YBa2Cu3O7. Superconductor Science and Technology, 9, pp. 1–7.
- Brandt, E H (1991) Penetration of magnetic ac fields into type-II superconductors. Physical Review Letters, 67, pp. 2219–2222. doi.org/10.1103/PhysRevLett.67.2219.
- Kogan, V G & Nakagawa, N (2021) Current distributions by moving vortices in superconductors. Physical Review B, 103, p. 134511. doi.org/10.1103/PhysRevB.103.134511.
- Kogan, V G & Nakagawa, N (2021) Moving vortices in anisotropic superconductors. Physical Review B, 104, p. 094523. doi.org/10.1103/PhysRevB.104.094523.
- Villarreal, C & Caballero-Benitez, S.F (2019) Casimir forces and high-Tc superconductors. Physical Review A, 100, p. 042504. doi.org/10.1103/PhysRevA.100.042504.
- Castillo-Lopez, S. G., et al. (2021) Role of electronic relaxation rates in the Casimir force between high-Tc fuperconductors. Universe, 7, p. 69. doi.org/10.3390/universe7030069.
- Moser, E. K., et al. (1994) Microwave properties of YBa2Cu307−x films at 35 GHz from magnetotransmission and magnetoreflection measurements. Physical Review B, 49, pp. 4199–4208. doi.org/10.1103/PhysRevB.49.4199.
- Coffey, M W & Clem, J R (1991) Magnetic field dependence of RF surface impedance. IEEE Transactions on Magnetics, 27, pp. 2136–2139. doi.org/10.1109/20.133634.
- Coffey, M W & Clem, J R (1991) Unified theory of effects of vortex pinning and flux creep upon the rf surface impedance of type-II superconductors. Physical Review Letters, 67, pp. 386–389. doi.org/10.1103/PhysRevLett.67.386.
- Coffey, M W & Clem, J R (1993) Theory of microwave transmission and reflection in type-II superconductors in the mixed state. Physical Review B, 48, pp. 342–350. doi.org/10.1103/PhysRevB.48.342.
- Lifshitz, E M (1956) The theory of molecular arrtactive forces between solids. Soviet Physics, Journal of Experimental and Theoretical Physics, 2, pp. 73–83. doi.org/10.1016/B978-0-08-036364-6.50031-4.
- Greenaway, D. L., et al. (1969) Anisotropy of the Optical Constants and the Band Structure of Graphite. Physical Review, 178, pp. 1340–1348. doi.org/10.1103/PhysRev.178.1340.
- Tinkham, M (1956) Energy gap interpretation of experiments on infrared transmission through superconducting films. Physical Review, 104, p. 845. doi.org/10.1103/PhysRev.104.845.
- Kubo, R (1957) Statistical-mechanical theory of irreversible processes. I. general theory and simple applications to magnetic and conduction problems. Journal of the Physical Society of Japan, 12, pp. 570–586. doi.org/10.1143/JPSJ.12.570.
- Wu, D H & Sridhar, S (1990) Pinning forces and lower critical fields in YBa2Cu3Oy crystals: Temperature dependence and anisotropy. Physical Review Letters, 65, pp. 2074–2077. doi.org/10.1103/PhysRevLett.65.2074.
- Bonn, D. A., et al. (1988) Far-infrared properties of ab-plane oriented YBa2Cu3O7. Physical Review B, 37, pp. 1574–1579. doi.org/10.1103/PhysRevB.37.1574.
- Coffey, M W & Clem, J R (1992) Theory of rf magnetic permeability of type-II superconductors in slab geometry with an oblique applied static magnetic field. Physical Review B, 45, pp. 10527–10535. doi.org/10.1103/PhysRevB.45.10527.
- Bezerra, V. B., et al. (2001) Surface impedance and the Casimir force. Physical Review A, 65, p. 012111. doi.org/10.1103/PhysRevA.65.012111.
- Gong, T., et al. (2021) Recent progress in engineering the Casimir effect? Applications to nanophotonics, nanomechanics, and chemistry. Nanophotonics, 10, pp. 523–536. doi.org/10.1515/nanoph-2020-0425.
- Chen, F., et al. (2007) Control of the Casimir force by the modification of dielectric properties with light. Physical Review B, 76, p. 035338. doi.org/10.1103/PhysRevB.76.035338.
- Iannuzzi, D., et al. (2004) Effect of hydrogen-switchable mirrors on the Casimir force. Proceedings of the National Academy of Sciences of the United States of America, USA, 101, pp. 4019–4023. doi.org/10.1073/pnas.0400876101.