This article explores the Hall effect and its effect in single and bilayer graphene systems.

Image Credit: NEW-LIGHT-VISUALS/Shutterstock.com
Bi-Layer Graphene
Bi-layer graphene (BLG) consists of two layers of single-layered graphene (SLG) with sp2-hybridized carbon atoms arranged in a two-dimensional hexagonal lattice structure. In comparison to SLG, which has a zero bandgap, the bandgap of BLG can be controlled using an external electric field.
The presence of a bandgap (i.e. difference in energy states) between two closely packed graphene layers facilitates ultrafast electron and ion conduction across the layers. With the added advantages of SLG, namely, large specific surface area (2630 m2.g-1), high thermal conductivity (5000 W.m-1. K-1), high light transmittance (97.7%), and high carrier mobility (106 m.s-1), BLG offers controlled transverse electronic superconductivity.
In recent research, the discovery of a quantum anomalous Hall effect (QAHE) in bilayer graphene has opened up a new path to quantize this bandgap and control the superconductivity more effectively.
According to the relative positions of carbon atoms and angles of the axis of the two layers of graphene, BLG is mainly divided into three categories: AA-stacked BLG, AB-stacked BLG, and twisted BLG. In AA-stacked BLG, two layers are arranged in such a way that each atom in the upper sheet is located exactly on top of the atom in the lower sheet with a layer spacing of 3.6 Å.
In AB-stacked BLG, only half of the atoms on the top sheet are above the atoms and the other half is above the center of the hexagons in the lattice of atoms and has a layer spacing of 3.4 Å, which is very close to graphite (normally 3.346 Å). Hence, the thermodynamic stability of AB-stacked BLG is better than that of AA-stacked BLG and twisted BLG.
Quantum Anomalous Hall Effect
In classical physics, the Hall effect (HE), discovered in 1879 by Edwin H. Hall, is defined as the generation of a transverse electrical field (potential difference) across the width of a conductor, when an external magnetic field is applied perpendicular to the direction of electric current passing through the conductor. The generated electrical field is perpendicular to both the magnetic field and the direction of electric current, and proportional to the product of the current density and the magnetic induction.
The cause of the Hall effect can be explained by the bending of electric field lines (path of charge carriers) due to Lorentz force, which leads to a variation of electric flux (density of electric field lines) across the width of the conductor.
Subsequently, Edwin H. Hall himself detected an anomaly to the Hall effect in ferromagnetic materials in which an additional component of the Hall voltage was found, which was proportional to the localized magnetization M and originated from the spin-orbit coupling of electrons. The quantum HE (QHE) and QAHE extend this phenomenon to a quantized version of two-dimensional electron systems under low temperatures and strong magnetic fields. The quantized values of quantum anomalous Hall resistance (R) are expressed by:
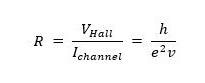
where, VHall = Hall voltage, Ichannel = channel current, e = electronic charge, h = Planck’s constant, and v = constant values roughly but not exactly equal to the filling factor of Landau levels. The conductivity (σ) = 1/R.
QAHE in BLG
Researchers have studied the quantum anomalous Hall effect in SLG and BLG systems with strong Rashba spin-orbit interactions due to externally controlled inversion symmetry breaking, and strong exchange fields due to proximity coupling to a ferromagnet. For BLG, an external gate voltage can introduce an inversion symmetry breaking gap, which results in a quantized Hall conductivity at neutrality twice that of SLG when the potential difference is smaller than the exchange coupling M. A sizeable Rashba spin-orbit coupling can be induced by the surface deposition of heavy-nucleus magnetic atoms, whereas the exchange field that can be introduced through a proximity effect.
Moreover, it has been predicted that BLG has five families of competing ground states by applying small external electric and magnetic fields as well as controlling the sign of charge carriers, the most stable states of the material occur at a temperature near absolute zero (-273.15 ℃ or -459.67 ℉). These states are driven by the mutual spin, and the orbital interaction of electrons is governed by quantum statistics and quantum mechanics, which facilitates the tunability of BLG bandgap and superconductivity.
References and Further Reading
Yuli, H., Xiaoyun, L., Huijuan, C., Zhen, Z., Bi-layer Graphene: Structure, Properties, Preparation and Prospects, Current Graphene Science (Discontinued) 2018; 2(2).
Wang-Kong Tse, Zhenhua Qiao, Yugui Yao, A. H. MacDonald, and Qian Niu, Quantum anomalous Hall effect in single-layer and bilayer graphene
Phys. Rev. B 83, 155447(2011) https://news.utdallas.edu/science-technology/graphene-quantum-hall-effect-2021/
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.