In quantum mechanics, a system’s wavefunction captures everything we can know about its state, holding all the essential information needed to describe it at the quantum scale. These quantum states are key to enabling precise manipulations at the quantum level, capabilities that underpin quantum computing in today’s most advanced supercomputers. This article explores the theoretical and mathematical foundations of quantum states and wavefunctions and highlights their role in driving modern applications.

Image Credit: agsandrew/Shutterstock.com
The Mathematical Description: What is a Wavefunction?
The wavefunction is a critical mathematical function describing the quantum state of a system. The wavefunction is represented using psi (Ψ), and encodes all the information about any quantum system in a probabilistic manner.
At the heart of quantum mechanics is its probabilistic nature, captured through the wavefunction. Quantum mechanics doesn’t predict the exact outcome of any event, or the exact state of any physical system; rather, it gives us the probabilities of various viable outputs or the probability of occurrence of a viable quantum states of the system.
Download your PDF copy now!
Born Rule: A Key Mathematical Interpretation of Quantum Mechanics and Probabilistic Amplitude
This key mathematical relationship between quantum mechanics and probability was devised by Max Born. To simply explain Born’s rule, consider a wavefunction Ψ (x, t), and the probability of finding a particle between the positions x and x + dx is represented by:
∣Ψ(x,t)∣2 dx
Following this concept, ∣Ψ(x,t)∣2 is described as the probability density, also expressed as the probability per unit length. For any wavefunction representing a physical system with a finite integral 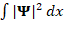 can be normalized to have the total probability 1.
can be normalized to have the total probability 1.
According to the Born postulate, just as the probability of all possible outcomes must sum to 1, the total probability of finding a particle anywhere along the real axis, or of observing a particular quantum state, must also equal one.1
∣∣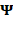 ∣∣2 =
∣∣2 = 
In a more detailed manner, the quantum state of any observable quantity on a Hilbert space H with real and unique eigenvalues 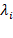 and Eigen vectors {
and Eigen vectors { }, such that
}, such that  =
= , can be represented by the wavefunction ψ, which can be represented as:
, can be represented by the wavefunction ψ, which can be represented as:
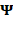 =
= 
Here (,) represents the internal product or the overlap between states, and 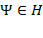 is a unit vector in the pure state. As per the Born rule, for any physical system in the quantum state
is a unit vector in the pure state. As per the Born rule, for any physical system in the quantum state  , the probability for obtaining any particular eigenvalue of any quantum observable is given by:
, the probability for obtaining any particular eigenvalue of any quantum observable is given by:
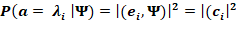
Importance of Schrödinger’s Equation
The use of Schrödinger equation allows physicists to calculate the wave function ψ (r,t) of a particle in Hilbert space, based on a potential V(r,t), which can vary with position r and time t.
Solving the Schrödinger equation gives a range of possible wave functions, along with the possible quantum states and energy levels that correspond to electron behavior. Notably, the equation also involves complex numbers (much like the quantum wavefunction) which makes it possible to determine quantum states and address problems in quantum mechanics.3
Quantum States: Pure vs Mixed
A quantum system can be represented as a unit ray in Hilbert space, with its density matrix serving as the quantum counterpart of a probability distribution. While in particular cases, it provides complete quantum information, it is also useful in expressing the probabilistic ensemble of the system, representing the uncertainties in a few instances.
Pure states are essential in providing the complete picture at the quantum level. If we consider 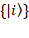 to be the complete orthonormal basis in the Hilbert space, the quantum state
to be the complete orthonormal basis in the Hilbert space, the quantum state  =
=  is the pure quantum state, and its density matrix is the outer product
is the pure quantum state, and its density matrix is the outer product  . The vector
. The vector  also known as a ket with unit length in the complex Hilbert space, represents the pure state of quantum systems.
also known as a ket with unit length in the complex Hilbert space, represents the pure state of quantum systems.
In case of pure quantum states, the density operator  is Hermitian, and a projection operator satisfying the condition
is Hermitian, and a projection operator satisfying the condition  , implying it can only have a definite eigenvalue of either 0 or 1. For a pure quantum state, the trace of the density operator
, implying it can only have a definite eigenvalue of either 0 or 1. For a pure quantum state, the trace of the density operator  is equal to one.
is equal to one.
For mixed states, the properties associated with the density matrix, like the expectation value of an observable, and the post-measurement ensemble of quantum states, are not a linear combination of terms within Schrodinger’s equation.4 Instead of representing a superposition of the quantum states, the density matrix accurately describes the mixture of quantum states, representing the classical uncertainty.
The mixed quantum state has also been expressed using 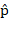 , where the mixture of states is written as
, where the mixture of states is written as  . Here,
. Here,  represents a set of mixtures of quantum states, and the number N is any number not limited by the Hilbert space.5
represents a set of mixtures of quantum states, and the number N is any number not limited by the Hilbert space.5
The Relationship of Wavefunction Collapse and Quantum Decoherence to Quantum Measurement
When a certain quantum observable, such as position or momentum, is measured, the system is transformed into a state where that observable is well-defined and has the highest probability of occurrence. This occurs when the wavefunctions describing the quantum state of the physical system collapse, and this process is known as the state collapse.
Wavefunction collapse occurs due to the transition of a system from a superposition of states to a wavefunction that completely represents only one of these states. In case of measuring the spin of any charged particle like an electron, the interaction of the particle with the Stern-Gerlach measuring apparatus will lead to a wavefunction collapse into one that represents either a spin-up state or a spin-down state, but no longer both.
The interference of waves occurs due to their inherent attributes, giving rise to the ability of the system to exist in several states at the same time. This property of waves, known as coherence, is when waves are locked with each other with a constant phase difference. Quantum decoherence occurs when the constant phase difference is removed.
During decoherence, the quantum feature of superposition, where a system can have many possible values for a certain property, is lost. As a result, the wavefunction collapses into a state where that property has a specific, well-defined value.6
Further Reading
- The University of Edinburgh (2012). Quantum States. Lecture 1. [Online]. Available at: https://www2.ph.ed.ac.uk/~ldeldebb/docs/QM/lect1.pdf [Accessed on: July 18, 2025].
- Landsman, N.P. (2022). The Born rule and its interpretation. Radboud Universiteit. 1-2. [Online]. Available at: https://www.math.ru.nl/~landsman/Born.pdf [Accessed on: July 19, 2025].
- Levada, C. et. al. (2018). Review of the Schrödinger Wave Equation. IOSR Journal of Applied Chemistry. 11(4), 01-07. Available at: https://www.iosrjournals.org/iosr-jac/papers/vol11-issue4/Version-1/A1104010107.pdf
- Patel, A. (2023). The Quantum Density Matrix and Its Many Uses. J Indian Inst Sci 103, 401–417. Available at: https://doi.org/10.1007/s41745-023-00406-4
- The University of Oregon. (2009). Mixed states and pure states. 1-14. [Online]. Available at: https://pages.uoregon.edu/svanenk/solutions/Mixed_states.pdf [Accessed on: July 20, 2025].
- The University of Southampton. (2013). Wavefunction Collapse. Chapter 12. 1-4. [Online]. Available at: https://www.southampton.ac.uk/~doug/quantum_physics/collapse.pdf [Accessed on: July 20, 2025].
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.