A paper recently published in the journal AppliedMath investigated the information loss phenomenon in the Lipkin model, a many-fermion system.
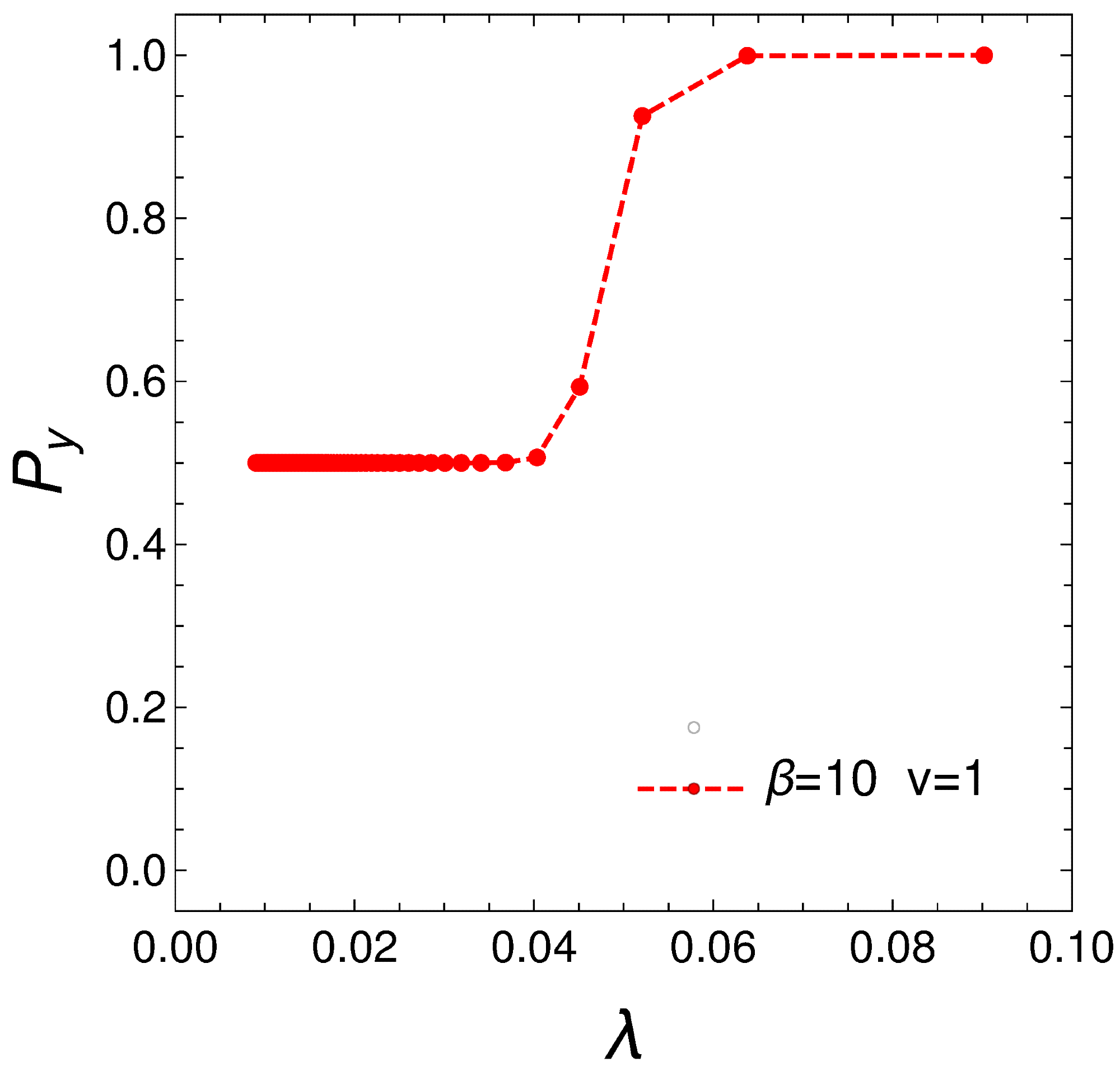 Purity versus de Broglie thermal wavelength (in meters) for β=10, N=20, v=1. When the purity is small, the wavelength is also small, and vice versa when the purity approaches unity. One detects a minimum purity equal to one-half (see text). Image Credit: https://www.mdpi.com/2673-9909/4/2/31
Purity versus de Broglie thermal wavelength (in meters) for β=10, N=20, v=1. When the purity is small, the wavelength is also small, and vice versa when the purity approaches unity. One detects a minimum purity equal to one-half (see text). Image Credit: https://www.mdpi.com/2673-9909/4/2/31
Quantum Mixture and Classical Behavior
The quantum mixture is crucial in quantum mechanics as it reflects the quantum systems' intrinsic probabilistic nature and enables the description of these systems' statistical behavior. The presence of superposition states and the related quantum entanglement concept is one of the key features of quantum mechanics.
In quantum mechanics, systems can simultaneously exist in several states, which is known as superposition. A quantum mixture is primarily a probabilistic combination of these states and allows the description of a system's overall state when the system is not in a pure state.
Thus, quantum mixture is a critical tool for developing quantum technologies, understanding correlations, and making predictions. Specifically, mixed states provide a more realistic and complete description of physical states than pure states.
Mixed states play a key role in characterizing the quantum communication protocol and quantum algorithm performance in quantum information theory. They provide a link between the real-world quantum systems' practicalities and the idealized pure states' concept. The loss of quantum effects/quantum characteristic behaviors with the increasing number of particles is a well-documented phenomenon.
Specifically, the behavior of several quantum systems resembles classical behavior when the number of fermions collectively becomes very large, which is referred to as the correspondence principle. On a macroscopic scale, a large number of quantum particles' statistical comportment then resembles classical behavior.
The Study
In this study, researchers examined the quantum mixture concept from the perspective of interacting many-fermion systems. Specifically, the phenomenon of information loss measured using the Kullback-Leibler divergence was investigated in a many-fermion system/the Lipkin model.
The objective was to study the quantum mixtures' peculiarities in the Lipkin model, an exactly solvable model of (N) interacting fermions of mass (m), using information theory tools. Information losses that occur when N increases from an earlier, lower reference fermion number (N₀) were measured using the Kullback-Leibler divergence.
The Lipkin model is well-known in nuclear physics and for quantum many-body systems, specifically for studying the interplay between quantum phase transitions and pairing correlations. This model can offer crucial insights into the complex quantum systems' behavior and provides simplified settings that can be used to analytically explore fundamental quantum principles.
Researchers commonly use the Lipkin model to test and develop new theoretical frameworks, like quantum field theory and many-body techniques. In this work, researchers primarily focused on exploring the quantum mixture-particle number N relationship using information theory tools.
Information theory provides a formalism for understanding and quantifying information content, entropy, and correlations in physical systems. Key concepts include conditional entropy, mutual information, and entropy. These tools can be utilized to analyze the relationships between various parameters in a quantum system and provide insights into the entanglement, correlations, and complexity that exist within the system.
Thus, this interdisciplinary approach, combining quantum statistical mechanics, information theory, and the Lipkin model, can provide an effective framework for assessing the complex connections between special statistical quantifiers and model traits.
Researchers used very low temperatures, which is a common statistical mechanics technique for approximating a system's ground-state properties. This robust approach exploits the relationship between a system's ground state and low-temperature properties. The values corresponding to the inverse temperature β = 10 or 20 were taken as low temperatures T for this work, with β = 1/kT and k being the Boltzmann constant.
Significance of the Findings
In this work, the researchers encountered various ways of visualizing the difference between pure and mixed states and introduced a new quantifier for the quantum mixture degree, referred to as de Broglie thermal length (λ), which could be cast as a length. As per the research, systems with λ-values greater than 12 cm indicated purity equal to unity, while smaller values indicated rising degrees of state mixing.
λ values smaller than 0.001 mm indicated the remnants of classical behavior. Thus, λ, a pseudo thermal length, was an effective purity indicator for the Lipkin model. Additionally, the system purity diminished rapidly at a finite temperature T when the fermion-fermion interaction degree became larger.
At a finite temperature, the growth of N increased the degree of mixture in the Lipkin model. Information loss was observed, as measured by the Kullback-Leibler divergence, when N was augmented. Thus, the information loss was higher for larger mixture degrees. However, the information loss was extremely small in the case of pure states at zero temperature.
To summarize, the findings of this study demonstrated that significant loss of information occurs when the system/the Lipkin model is in a mixed state, while the loss almost disappears when the system is in a pure state.
Journal Reference
Monteoliva, D., Plastino, A., Plastino, A. R. (2024). Quantum Mixtures and Information Loss in Many-Body Systems. Applied Math, 4(2), 570-579. https://doi.org/10.3390/appliedmath4020031, https://www.mdpi.com/2673-9909/4/2/31
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.
Article Revisions
- May 15 2024 - Title changed from "Quantum Mixtures and Information Loss in the Lipkin Model" to "Decoding Quantum Mixtures with the Lipkin Model"