Tensor networks have been recognized as an effective representation and research tool for quantum systems. Tensor network-based algorithms are used to explore the basic properties of quantum systems.

Image Credit: sakkmesterke/Shutterstock.com
Tensor network techniques are becoming important in contemporary quantum mechanics and other fields. They offer effective approximations for a particular class of quantum states, and the graphical language used to describe them makes it simple to explain and reason about quantum circuits, protocols, and open systems, among other physical phenomena.
Tensors
The concept of multilinear mappings, or functions with many parameters that are linear with respect to each parameter, is encapsulated and generalized in mathematics as tensors. A countable group of tensors joined together by contractions is what is known as a tensor network. The complete group of related techniques, which are often used in contemporary quantum information science, mathematics, computer science, and condensed matter physics, is collectively referred to as tensor network methods.
An easy-to-use graphical language is provided with tensor networks that may be used to understand their concepts better. This diagrammatic language has been around since at least Roger Penrose's work in the early 1970s. Many improvements and adjustments to various physics, math, and computer science fields have been made to these techniques. David Deutsch's adoption of the diagrammatic notation in quantum computing and the creation of the quantum circuit was a significant turning point in the advancement of quantum computing.
A unique class of tensor networks called quantum circuits has constrained tensor types and arrangements. The quantum circuit model, which has been around for more than two decades, is frequently used to explain quantum algorithms and their experimental implications, quantify the resources they use, for example, by counting the number of quantum gates needed, categorize the entangling characteristics and computing power of particular gate families, and more.
Tensors are arrays of numbers in several dimensions. They may be thought of as a generalization of matrices, scalars, and vectors. Tensors can be characterized in terms of their rank, indices, and index dimension. A tensor's rank, which is determined by the number of indices it contains, is zero for scalars, one for vectors, and two for matrices. The number of possible values for an index is its dimension. One index, for instance, can hold three different values in a vector with three elements. As a result, this vector is a rank one tensor, and the associated index has three dimensions.
Tensor Contractions
It's crucial to comprehend tensor contraction before defining tensor networks. By adding up several indices, more than two tensors can be contracted. The repeated indices are shown in diagrammatic notation as lines joining tensors, as shown in Figure 1 below. Two two-rank tensors are linked by a single repeating index. The bond dimension is the dimension of the repeating index.
Tensor Networks
A group of tensors that have all of their indices contracted together is known as a tensor network. As previously indicated, by linking separate tensors with lines, the diagrammatic notation is used to define which indices and tensors are contracted together. Tensor networks are capable of representing complex processes utilizing several tensors and a variety of indices contracted in creative ways.
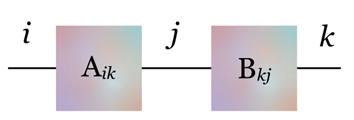
Figure 1. Diagrammatic notation of tensors
Tree tensor networks (TTN) and matrix product states (MPS) are two popular tensor network topologies. These can be expanded to have many or few indices and follow specified patterns of tensor connections. The image below shows examples of these designs using just a few tensors.
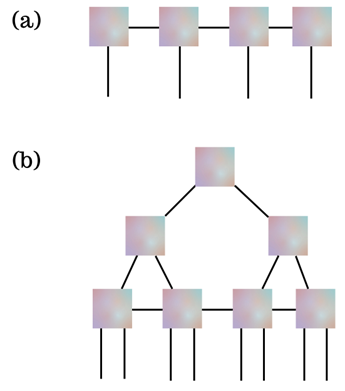
Figure 2 (a) Matrix product states (MPS) and (b) Tree tensor networks (TTN)
It is standard practice to employ these tensor networks to effectively describe certain many-body quantum states. A tensor network may be used to represent any quantum circuit, with the bond dimension depending on the circuit's width and connectedness. Additionally, it is possible to create quantum circuits with connections similar to popular tensor networks like MPS and TTN. These are referred to as tensor-network quantum circuits.
It should be noted that a tensor network's connectedness depends on the distribution of entanglement and the dispersion of correlations in the resultant tensor-network quantum circuit. In order to better capture the information that is being extracted, circuits based on tensor networks are developed.
The tensor network architecture serves as a template for the geometry of the quantum circuit in tensor-network quantum circuits. To create quantum circuits, the tensors in the tensor networks mentioned above are expressly substituted with unitary operations.
Outlook
Tensor networks are a promising foundation for quantum computing because they have many of the characteristics that make them appealing to conventional algorithms. Tensor networks offer a natural hierarchy of ever more complicated quantum states, enabling one to select the right number of resources for a particular job. They also make it possible for specialized algorithms to process highly dimensional data with fewer qubits, which is an efficient use of precious resources. The parameters of a more potent model built on quantum technology can be initialized using an optimized, classically tractable tensor network.
More from AZoQuantum: Quantum Speed Limit of a Single Atom Trapped in a Fabry-Perot Microresonator
References and Further Reading
Biamonte, J. & Bergholm, V. Quantum tensor networks in a nutshell. (2017). arXiv:1708.00006
Diego Guala , Esther Cruz-Rico , Shaoming Zhang , Juan Miguel Arrazola. (27 June 2022) Tensor-network quantum circuits. Pennylane.ai. Available online: https://pennylane.ai/qml/demos/tutorial_tn_circuits.html
W. Huggins, P. Patil, B. Mitchell, K. B. Whaley, and E. M. Stoudenmire, Quantum Science and Technology 4, 024001 (2019), ISSN 2058-9565, URL http://dx.doi.org/10.1088/2058-9565/aaea94
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.