Controlling Qubits: What is Superconducting Qubit Characterization?

By exploiting quantum physical phenomena, quantum computing promises an advance in numerical processing power of traditional computing^1,2. The current experimental work being undertaken in this field focuses on improving the devices that would ultimately perform the function of transistors in classical processors. These are the quantum bits – qubits.

Superconducting qubits are one of the most promising contenders that are currently studied^3,4. They are based purely on microfabrication technology and electrical control so superconducting qubits have a clear roadmap for large-scale integration of hundreds of qubits in one single processor.

There is confidence that the devices can be engineered to a quality that supports practical numerical algorithms and this is supported by the steady improvement of coherence times achieved over the last few years.

Growing Complexity

In order to control superconducting qubits, complex pulsed microwave signals on multiple channels with accurate synchronization are required. Standardized, highly reliable and integrated electronic control solutions are essential with the increased in the number of qubits and channels. Zurich Instruments UHFLI instrument addresses this demand because it contains a 600 MHz lock-in amplifier equipped with a digitizer for detection and an arbitrary waveform generator (AWG) that synthesizes precisely shaped pulsed signals.

By combining detection and generation in one device, synchronization can be improved, the setup complexity and rack space can be reduced, and advanced control methods can be used based on feed-forward from detection to generation, for example, sequence branching.

This article discusses how the UHFLI instrument can be used to characterized superconducting qubits in terms of qubit state lifetime, frequency and coherence time. Tuning the pulse shapes that are used to generate quantum computing sequences is also provided by the measurements that are presented in this article.

The circuit quantum electrodynamics architecture⁵ can be extended to the multi-qubit experiments and was used to perform the experiments mentioned in this article. Measurements were performed in Zurich, Switzerland, in Prof A Wallraff’s Quantum Device Lab.

Setup and Sample

To enable readout and control of a qubit’s quantum state, quantum computing devices are developed. Generally, the quantum state is a quantum superposition of two physical configurations of the qubit device and encodes the data processed in a quantum computer.

Figure 1(a) shows the sample which consists of aluminum- and niobium- based resonant circuits on a sapphire chip. The qubit shown in the inset is a nonlinear resonator which is formed of an on-chip capacitor (orange in the picture) and a small superconducting quantum interference device (SQUID).

The qubit is tunable over a frequency range from 4 to 7.5 GHz due to the SQUID design which applies a small magnetic field to the device.

Figure 1. (a) Optical micrograph of the sample showing the readout resonator (blue) and the qubit capacitor plates (orange). The resonator is coupled to input and output lines via a Purcell filter ^[6] (cyan). Insets show magnified views of the qubit and the coupler between resonator and Purcell filter. (b) Simplified diagram of the experimental setup based on the UHFLI instrument integrating a lock-in amplifier and an AWG. The superconducting qubit sample is cooled in a dilution refrigerator.

The external signals are guided directly to the qubit for its control by a coplanar waveguide (green). The qubit is coupled with a coplanar-waveguide resonator (shown in blue)⁵ at 4.78 GHz. The readout resonator is connected to a pair of coaxial cables that provided the interface for reading out the quantum state of the qubit by an on-chip filter.

A schematic of the measurement setup, in which the sample is placed in a dilution refrigerator to provide a low-temperature well isolated environment to protect the quantum properties of the sample, is seen Figure 1(b).

In order to generate control pulses, quadrature modulation of a microwave signal is performed with two AWG channels. The pulses for a qubit readout are helped to generate by feeding one of the AWG marker channels to the gate input of a signal generator.

After the pulses are transmitted through the readout resonator, they are amplified, and the readout signal is then down-converted to an intermediate frequency f_IF. Subsequently, one of the UHFLI lock-in amplifier channels is used to measure the pulses.

Measurements

Qubit Spectroscopy

Firstly, the spectroscopic measurements of the line-width and frequency of the qubit and the readout resonator are measured. A small coil at the sample is used to set up the optimum magnetic field bias, this can also be determined using spectroscopy.

A continuous microwave tone is applied to a resonator in order to measure the readout resonator. The amplitude of the down-converted transmitted signal is measured with the lock-in amplifier. The tone’s frequency v_res is swept across the frequency f_res of the resonator and one such measurement is shown in Figure 2(b). The result of the on-chip Purcell filter is that the resonator’s transmission lineshape is a narrow dip at f_res on top of a broader peak⁶.

To measure the qubit transition frequency, a two-tone microwave technique was used. The first microwave tone is applied to the readout resonator at a fixed frequency clos to resonance f_res. A second tone is applied to the gate line of the qubit and while the transmission amplitude is measured, its frequency v_qb is swept across a broad range.

There is a change when v_qb becomes resonant with the qubit transition at f_qp due to the dispersive coupling between the readout resonator and qubit⁵. This results in a feature at f_qb and this is shown in (a).

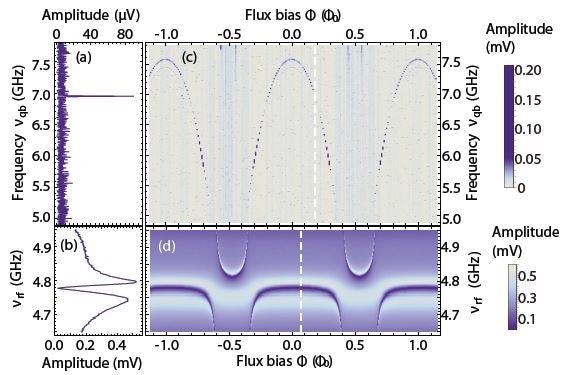
Figure 2. Spectra of the qubit (a) and of the readout resonator (b). The measurement in (a) is obtained by measuring the transmission at a fixed frequency ν_rf close to the cavity resonance (b) and sweeping the qubit drive frequency ν_qb. (c) The arc-shaped dependence on magnetic flux F is characteristic for this type of qubit. As the qubit frequency crosses the frequency of the readout resonator along the horizontal axis in (d), the two exhibit an avoided crossing. The color scale shows the amplitude of the signal transmitted through the readout resonator after amplification.

The qubit and resonator spectra can be seen as a function of magnetic field in Figure 2(c) and (d). The characteristic arc-shaped dependence on magnetic field is the exhibition of the qubit transition⁷. An avoided crossing is exhibited by the readout resonator and the qubit and this can be seen in (d). This vacuum Rabi splitting is caused by the strong coupling between the resonator and the qubit.

The subsequent measurements are pulsed rather than continuous in order to probe the qubit’s dynamic properties. The basis of these measurements is a pulse sequence that consists of a control part and a readout part. During the control part, pulses are applied to the qubit gate line at a frequency close to f_qb.

The resonant pulses result in Rabi oscillations which are a coherent oscillation of the qubit between its excited state and its ground state. A pulse is applied to the readout resonator at a frequency close to f_res after the control part and, after transmission through the sample, a trigger measurement of the signal is performed.

The return signal is first down-converted in the analog domain to f_IF = 28.125 MHz in order to achieve this. It is then demodulated in the digital domain using the lock-in amplifier. The measurement is protected from amplifier offset voltage drift and 1/f noise using digital lock-in technology instead of direct down-conversion to DC⁸.

The entire cycle is repeated several thousand times to average out quantum fluctuations and increase the signal-to-noise ration. The averaging of raw data is conventionally done before the down-conversion. However, down-conversion can be performed before the averaging by using the UHFLI’s digital demodulators.

This method eliminated the need to choose an intermediate frequency that is commensurate with the repetition rate and removes one data post-processing step from the experiment. It is also imperative during the implementation of feed-forward protocols, where the demodulated signal must be quickly available.

Rabi Oscillations

Applying a control pulse results in a distinct change in the qubit state. This can be used in a single-qubit gate operation. These operations are imperative for implementing quantum computing algorithms in a similar way that classical computing algorithms require logical inversion. Rabi oscillation measurement can be used to determine the parameters for a given gate operation.

For this measurement, a flat plateau with a variable width and a control pulse with an envelope shaped by smooth edges (rise/fall time 3.9 ns) are generated. Following this control pulse is a readout pulse, which is a microwave burst which has an approximately rectangular envelope.

The probability that the qubit will be in the excited state follows a sinusoidal evolution as a function of the control pulse area and this is also proportional to its width at half maximum. Figure 3 plots the signal measured during the readout phase and this reflects the evolution.

The width of the qubit gate pulses relevant for the next measurements to be identified can be found using the curve: the Π/2-pulse width corresponds to the first quarter period and the Π -pulse width corresponds to the first maximum. The Π/2-pulse brings the qubit to an equal coherent superposition of ground and excited state whilst the Π-pulse brings the qubit from ground to its excited state. For this measurement, all control pulses were repeated at a rate of 13 kHz, 4000 times.

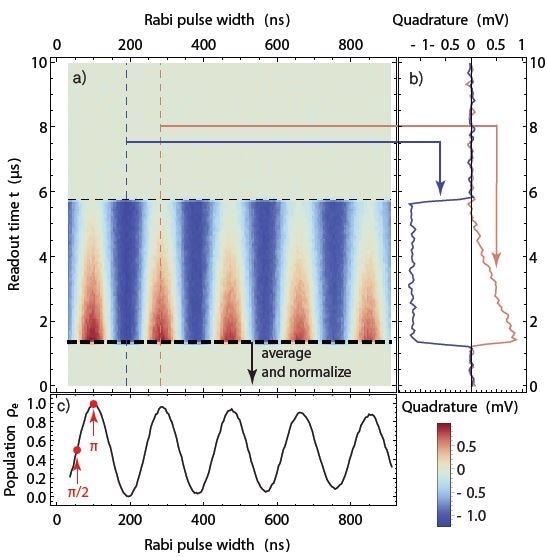
Figure 3. Rabi oscillation measurement. As a function of the width of the control pulse, the qubit evolves periodically from ground state to excited state and back. This results in a sinusoidal readout signal amplitude as a function of the pulse width (horizontal axis) as seen in the color plot in (a). (b) Time-dependent readout signal at two values of the pulse width marked in (a). The time between about 1.2 µs and 5.8 µs corresponds to the readout pulse. (c) Rabi oscillation plot obtained by averaging the data in (a) and normalizing the result to obtain a mean excited-state population. The measurement allows us to determine the parameters for Π- and Π/2-pulses (red marks).

Qubit Lifetime

Due to the decay from the excited qubit state to the ground state, the duration of a computation algorithm is restricted. Therefore, measurement of the average lifetime T₁ is an important part of the device characterization.

A Π-pulse is applied at the beginning of the sequence when measuring the T₁. Then, there is a wait for a variable time t and finally, the qubit state is measured. The resulting data is shown in Figure 4. The lifetime T₁ = 8.8 ms has been extracted to fit an exponential exp(-t/T₁).

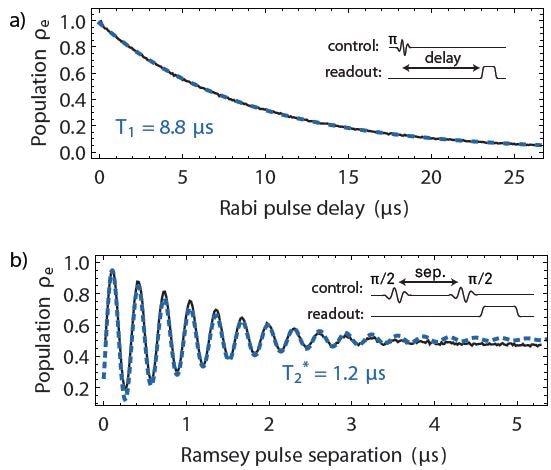
Figure 4. (a) Qubit lifetime T₁ measurement. The qubit is initialized in the excited state with a p-pulse. The subsequent exponential decay is then measured for increasing delays before the readout pulse. (b) Ramsey fringe measurement. As the delay between two p/2-pulses is varied, the qubit readout signal follows a decaying oscillatory evolution reflecting the gradual loss of phase coherence. The measurement is used to determine the qubit coherence time T₂*. Both measurements were averaged 40’000 times at a 27 kHz repetition rate.

Using the UHFLI’s control software LabOneâ, sequences and waveforms can be directly generated. The UHF-AWG was used to generate a series of 200 patterns by using a sequencer loop incrementing the readout pulse delay from 0 ms to 26 ms with run-time sequencer variables and dynamic waiting times.

As a result, all qubit control pulses can be generated from a single Π-pulse envelope that has less than 400 samples of waveform data for both channels. This is not the same as in conventional methods, where patterns for all pulse delays need to be uploaded to the AWG sample-by-sample which requires waveform data of about 200 x (26 µs) x (2 channels) x (1.8 GSa/s) = 18.7 MSa and, as a result, much longer waveform transfer time.

Qubit Coherence Time

The Ramsey fringe measurement shows the free coherent evolution of the qubit. In the Ramsey sequence there are two Π/2-pulses separated by varying delay time followed by a qubit readout. The two Π/2-pulses combine to form a full Π-pulse when there is no decoherence, and the qubit ends up in the excited state.

Dephasing and relaxation during the delay time mean that the pulse addition becomes imperfect. This means that, with time delay, the potential for being in the excited state decays. A beating effect between the qubit phase and the phase of the control pulse carrier is creased by a slight detuning of the pulse frequency relative to f_qb. This results in an oscillatory contribution in the readout signal. The dephasing time of T₂*=1.2 ms can be extracted from the measurement which is shown in Figure 4(b).

The pulses that are generated by the duel-channel AWG have intermediate frequency carriers at 112.5 MHZ. This is generated using the UHF-AWG modulation mode operating in the digital domain. The analog mixer is then used to upconvert the intermediate frequency to the qubit transition frequency. Using amplitude modulation means that the carrier and phase frequency can be swept or adjusted without reprogramming the AWG.

Conclusion

The potential of the Zurich Instruments’ UHFLI lock-in amplifier and AWG in an experimental domain that requires signal quality, high speed and timing precision, are demonstrated with these essential qubit measurements. These measurements can be used to obtain an in-depth characterization of a qubit instrument with regards to coherence time, operating frequency and its lifetime. More complex sequences for experiments such as echo spin or randomized benchmarking are set up in a straight-forward manner, based on the elementary pulses used for these measurements.

Acknowledgments

Zurich Instruments would like to thank Prof. Wallraff and the members of his Quantum Device Lab at ETH Zurich, Switzerland, where these measurements were carried out. Special thanks go to Michele Collodo. Thanks go to Theodore Walter for providing the qubit sample and Yves Salathé, Simone Gasparinetti, and Philipp Kurpiers for support with the measurements and for discussions. This work was supported by the Swiss Federal Department of Economic Affairs, Education and Research through the Commission for Technology and Innovation (CTI).

References

1. R. P. Feynman. Simulating physics with computers. Int. J. of Theor. Phys., 21:467, 1982.
2. T. D. Ladd, F. Jelezko, R. Laflamme, Y. Nakamura, C. Monroe, and J. L. O’Brien. Quantum computers. Nature, 464:45, 2010.
3. Y. Nakamura, Pashkin, Yu. A., and Tsai J. S. Coherent control of macroscopic quantum states in a single- Cooper-pair box. Nature, 398:786, 1999.
4. John Clarke and Frank K. Wilhelm. Superconducting quantum bits. Nature, 453:1031, 2008.
5. A. Wallraff, D. I. Schuster, A. Blais, L. Frunzio, R.- S. Huang, J. Majer, S. Kumar, S. M. Girvin, and R. J. Schoelkopf. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature, 431:1627, 2004.
6. M. D. Reed, L. DiCarlo, B. R. Johnson, L. Sun, D. I. Schuster, L. Frunzio, and R. J. Schoelkopf. High-fidelity readout in circuit quantum electrodynamics using the Jaynes-Cummings nonlinearity. Phys. Rev. Lett., 105:173601, Oct 2010.
7. Jens Koch, Terri M. Yu, Jay Gambetta, A. A. Houck, D. I. Schuster, J. Majer, Alexandre Blais, M. H. Devoret, S. M. Girvin, and R. J. Schoelkopf. Chargeinsensitive qubit design derived from the Cooper pair box. Phys. Rev. A, 76:042319, Oct 2007.
8. David Schuster. Circuit Quantum Electrodynamics. PhD thesis, Yale University, 2007.

This information has been sourced, reviewed and adapted from materials provided by Zurich Instruments.

For more information on this source, please visit Zurich Instruments.