Time dependent perturbation theory is a mathematical tool to derive approximate quantum solutions for a physical system that is affected by an external time dependent force. This article can be read in tandem with our piece: What is the Time Independent Perturbation Theory?
Image Credit: local_doctor/Shutterstock.com
A set of moving particles that have kinetic and potential energies is defined as a dynamical physical system. One method to study such a physical system mathematically is by using the Hamiltonian analysis.
The Hamiltonian
The Hamiltonian of a physical system is its total energy given by the sum of its kinetic and potential energies. First formulated by Sir William Rowan Hamilton in 1835 to describe classical physical systems, it was later adapted in the formulation of quantum mechanics.
In classical physics, the Hamiltonian can be represented as shown in the equation below.
H = K + V
Here, H denotes is the Hamiltonian, and K and V represent the kinetic and potential energies respectively.
The Hamiltonian representation is transformed to operators when applied in quantum mechanics. The kinetic and potential energy expressions are represented by operators as shown below.
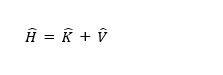
The Schrodinger Equation
The Schrodinger equation is a revolutionary development in quantum physics. It is a mathematical expression describing the energy and position of a particle. The Schrodinger equation is derived by applying the Hamiltonian operators on the wave function of a system. The solutions to the Schrodinger equation produce discrete values for the energy called energy eigenvalues.
Perturbation Theory
A quantum system is perturbed when an external force is introduced to the system. Under such perturbed conditions, exact quantum solutions are difficult to be derived using conventional methods. In such cases perturbation theory is a useful tool for obtaining approximate solutions. When the external interference is a uniform, time-independent force, time independent perturbation theory is applicable.
Perturbation theory only works when the scale of the applied external energy is relatively small when compared to the energy of the system under investigation. For example, an electric field encountered by a hydrogen atom is an ideal system to study perturbation theory. The addition of the external force distorts the original Hamiltonian as expressed in the equation stated earlier. This subtle change can be represented by a new, modified Hamiltonian as shown below:
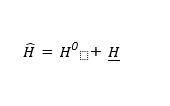
(hereby referred to in the text as H^, Ho, and H_, respectively)
Here, H^ is the new Hamiltonian, Ho is the original Hamiltonian that can be solved using the Schrodinger equation, and H_ is the perturbation that has been added. Perturbation theory is valid only if the solutions of the system where there is no perturbation are exactly known or derivable. So, in the above-modified equation, Ho has to be solvable.
To solve the new Hamiltonian H^, the quantum states are expanded as superpositions of the known solutions of the unperturbed Hamiltonian Ho. The perturbation is considered as the change in the solution states of Ho to a new perturbed state.
A power series expansion is used to analyze the energy of the perturbed state. The zeroth term of the series expansion is the unperturbed energy Ho and the following series terms correspond to the corrections required to arrive upon an approximate quantum solution for H^.
Time Dependent Perturbation Theory
When the perturbation is a time-varying force, the theory developed above is no longer applicable. The time dependent perturbation can now be written with the following modified Hamiltonian.

(hereby referred to in the text as H^, Ho, and H_(t), respectively)
Here the perturbation term H_(t) has a time dependence and as such does not have energy eigenstates. Typically, the time dependence H_(t) can be regarded as a perturbation that occurs for a finite time starting from an initial time, where the time is set to zero, to some arbitrary final time. For times, less than the initial time and for greater than the final time considered, H_(t) vanishes, resulting in solutions consistent with Ho. The time dependent perturbation is mathematically evaluated using the “interaction picture.”
The Interaction Picture
The interaction picture of quantum mechanics was developed to efficiently solve time dependent perturbations. The interaction picture, also called the Dirac picture, makes use of the Heisenberg formulation of quantum mechanics as well as Schrodinger's description based on the wave nature of matter.
In the Heisenberg picture, the quantum state is held fixed while the dependence of observables on time can be measured. While in the Schrodinger picture, time dependent observables are held fixed while the evolution of states can be analyzed over time. The interaction picture combines these two approaches mathematically to find solutions when a quantum system is perturbed by a time dependent force. This theory is established as the time dependent perturbation theory.
Examples Where Time Dependent Perturbation Theory is Applied
Nuclear magnetic resonance (NMR), ionization of an atom, the Helium atom, and auto-ionization, absorption, and stimulated emission, are some instances where the time dependent perturbation theory is used.
What is the Time Independent Perturbation Theory?
References and Further Reading
Griffiths, D., & Schroeter, D. (2018). Introduction to Quantum Mechanics (3rd ed.). Cambridge: Cambridge University Press. doi:10.1017/9781316995433
PAULING, L. AND WILSON, E. B. Introduction to quantum mechanics 2008 - Dover Publications - New York, N.Y.
Barton Zwiebach. Quantum Group| MIT OpenCourseWare| https://ocw.mit.edu| https://ocw.mit.edu/courses/8-06-quantum-physics-iii-spring-2018/89ef6d5958ee59bae9a91345c3d8c8e4_MIT8_06S18ch4.pdf
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.